
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ІІІ бөлім. Конус
|
|
Конус деп тік бұрышты үшбұрышты катетінен айналдырғанда шығатын фигураны атайды.
 V=
V=  R2H
R2H
Sб.б=  RL
RL
L2=H2+R2
Sт.б= Sб.б+Sтаб
 2003ж №1 (3 нұсқа №11) Конустың жасаушысы 2
2003ж №1 (3 нұсқа №11) Конустың жасаушысы 2  см-ге тең, осьтік қимасының төбесіндегі бұрышы 1200. Конустың табанының ауданын табыңыз.
см-ге тең, осьтік қимасының төбесіндегі бұрышы 1200. Конустың табанының ауданын табыңыз.
AC=2  см <ACB=1200 Sтаб-? АВ2=AC2+BC2-2AC*BC*cos1200
см <ACB=1200 Sтаб-? АВ2=AC2+BC2-2AC*BC*cos1200
АВ2= (2  )2+(2
)2+(2  )2+2*2
)2+2*2  *
*  =2*4*3+4*3=36
=2*4*3+4*3=36
AB=6 R=3 Sтаб=  R2 Sтаб=9
R2 Sтаб=9 
 №2 (3 нұсқа №29) Конустың биіктігі 4см. Табанының диаметрі 6см. Бүйір бетінің ауданын табыңыз.
№2 (3 нұсқа №29) Конустың биіктігі 4см. Табанының диаметрі 6см. Бүйір бетінің ауданын табыңыз.
CH=4см
AB=6см R=3cм Sб.б=  RL L2=H2+R2 L2=16+9=25 L=5
RL L2=H2+R2 L2=16+9=25 L=5
 Sб.б=
Sб.б=  *3*5=15
*3*5=15 
№3 (8 нұсқа №26) Конустың биіктігі табанының радиусына тең. Көлемі V=9  .Жасаушысын табыңыз.
.Жасаушысын табыңыз.
CH=R=x V=9  . L-? V=
. L-? V=  R2H
R2H  R2H=9
R2H=9  X3=27
X3=27
X=3 L2=H2+R2 L2=9+9=18 L=3 
 №4 (9 нұсқа №26) Конустың табанының радиусы 3
№4 (9 нұсқа №26) Конустың табанының радиусы 3  см, ал жасаушысы табан жазықтығына 450 бұрыш жасай көлбеген. Конустың көлемін және бүйір бетінің ауданын табыңыз. R=AH=3
см, ал жасаушысы табан жазықтығына 450 бұрыш жасай көлбеген. Конустың көлемін және бүйір бетінің ауданын табыңыз. R=AH=3  см <CAH=450 V, Sб.б-?
см <CAH=450 V, Sб.б-?
СH=3  см L2=H2+R2 L2=(3
см L2=H2+R2 L2=(3  )2+(3
)2+(3  )2 L2=36 L=6 V=
)2 L2=36 L=6 V=  R2H
R2H
V=  (3
(3  )3=18
)3=18 
 Sб.б=
Sб.б=  RL Sб.б=
RL Sб.б=  *3
*3  *6=18
*6=18 

№5 (13 нұсқа №27) Конустың көлемі 9 
 см3 Егер оның осьтік қимасы тең қабырғалы үшбұрыш болса, конустың биіктігін табыңыз. V=
см3 Егер оның осьтік қимасы тең қабырғалы үшбұрыш болса, конустың биіктігін табыңыз. V=  R2H V=9
R2H V=9 
 см3 9
см3 9 
 см3 =
см3 =  R2H
R2H
R=x, CB=2x CH2=4x2-x2=3x2 CH=  x
x  *x2*
*x2*  x=9
x=9 
 X3=27 X=3 CH=
X3=27 X=3 CH=  x=3
x=3 
 №6 (25 нұсқа №11) Осьтік қимасы тең бүйірлі тік бұрышты үшбұрыш болатын конус берілген. Тік бұрышты үшбұрыштың гипотенузасы 6
№6 (25 нұсқа №11) Осьтік қимасы тең бүйірлі тік бұрышты үшбұрыш болатын конус берілген. Тік бұрышты үшбұрыштың гипотенузасы 6  см-ге тең болса, бүйір бетінің ауданын табыңыз. AB=6
см-ге тең болса, бүйір бетінің ауданын табыңыз. AB=6 
R=3  H=3
H=3  L2=H2+R2 L2=(3
L2=H2+R2 L2=(3  )2+(3
)2+(3  )2 L2=36 L=6 Sб.б=
)2 L2=36 L=6 Sб.б=  RL
RL
 Sб.б=
Sб.б=  *3
*3  *6=18
*6=18 

2004 ж№7(5 нұсқа №30) Конустың жасаушысы табан жазықтығына 300бұрыш жасай көлбеген және 8 см-ге тең. Осьтік қимасының ауданын табыңыз. <CAH=300 AC=8 см SABC-? SABC=  AB*CH CH=
AB*CH CH=  AC CH=
AC CH=  *8=4 AH2=AC2-CH2 AH2=64-16=48 AH=4
*8=4 AH2=AC2-CH2 AH2=64-16=48 AH=4  AB=8
AB=8  SABC=
SABC=  AB*CH=
AB*CH=  *8
*8  *4=16
*4=16 
 №8 (13 нұсқа №30) Тең бүйірлі тік бұрышты үшбұрыш өзінің катетінен айналдырылған. Гипотенузасы 3
№8 (13 нұсқа №30) Тең бүйірлі тік бұрышты үшбұрыш өзінің катетінен айналдырылған. Гипотенузасы 3  см-ге тең болса, шыққан конустың көлемін табыңыз.
см-ге тең болса, шыққан конустың көлемін табыңыз.
AC=3  см
см
AC2=AH2+CH2
2AH2=18 AH2=9 AH=3 V=  R2H V=
R2H V=  *32*3=9
*32*3=9 
№9(19 нұсқа №30) Конустың биіктігі 15cм, ал көлемі 320  см3. Табанының радиусын табыңыз. V=
см3. Табанының радиусын табыңыз. V=  R2H V=320
R2H V=320  см3 H=15см
см3 H=15см  R2 *15=320
R2 *15=320  R2=64 R=8
R2=64 R=8
 2009ж №10(1 нұсқа №25) Жасаушысы L-ге, ал табанының радиусы R-ге тең конус берілген. Бір жағы конус табанында, ал қарсы жатқан жағының төбелері оның бүйір бетінде жататын конусқа іштей сызылған кубтың қырын табыңыз.
2009ж №10(1 нұсқа №25) Жасаушысы L-ге, ал табанының радиусы R-ге тең конус берілген. Бір жағы конус табанында, ал қарсы жатқан жағының төбелері оның бүйір бетінде жататын конусқа іштей сызылған кубтың қырын табыңыз.
PB=L BK=R, R-төртбұрышқа сырттай сызылған шеңбердің радиусы
a-? a-төртбұрыштың қабырғасы a=  R
R  H=
H= 
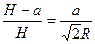 1-
1-  a (
a ( a=
a=  a=
a= 
 №11(3 нұсқа №18) Конустың осьтік қимасы тең бүйірлі үшбұрыш, бүйір қабырғасы 16 см, ал арасындығы бұрышы 1200 болса, толық бетінің ауданын табыңыз.
№11(3 нұсқа №18) Конустың осьтік қимасы тең бүйірлі үшбұрыш, бүйір қабырғасы 16 см, ал арасындығы бұрышы 1200 болса, толық бетінің ауданын табыңыз.
AC=16 см, <C=1200 Sт.б-? Sт.б=  R(R+L)
R(R+L)
АВ2=AC2+BC2-2AC*BC*cos1200 AB2=162+162+2*16*16*  =768 AB=16
=768 AB=16  R=AB:2 R=8
R=AB:2 R=8  Sт.б=
Sт.б=  R(R+L)=
R(R+L)= 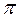 *8
*8  (8
(8  +16)=64
+16)=64 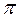 (3+2
(3+2  )
)
 №12(4 нұсқа №18) Тік конустың жасаушысы 6 см-ге тең және табан жазықтығына 600бұрыш жасай көлбеген. Толық бетінің ауданын табыңыз.
№12(4 нұсқа №18) Тік конустың жасаушысы 6 см-ге тең және табан жазықтығына 600бұрыш жасай көлбеген. Толық бетінің ауданын табыңыз.
AC=6 см, <A=600
Sт.б-?
Sт.б=  R(R+L)
R(R+L)  AH=6*
AH=6*  =3 см Sт.б=
=3 см Sт.б=  *3*(3+6)=27
*3*(3+6)=27 
 2010ж №13 (8 нұсқа №25) Конустың биіктігі 20-ға, табанының радиусы 25-ке тең. Конустың төбесі арқылы өтетін және конустың табанының центрінен қашықтығы 12 см-ге тең боатын қиманың ауданын табыңыз. SO=20 см, KO=25 см, PO=12 см SSKL=
2010ж №13 (8 нұсқа №25) Конустың биіктігі 20-ға, табанының радиусы 25-ке тең. Конустың төбесі арқылы өтетін және конустың табанының центрінен қашықтығы 12 см-ге тең боатын қиманың ауданын табыңыз. SO=20 см, KO=25 см, PO=12 см SSKL=  SP*KL
SP*KL  SEO; SE=
SEO; SE= 
 SPO; SO2=SE*SP SP= SO2:SE SP=400:16=25
SPO; SO2=SE*SP SP= SO2:SE SP=400:16=25  KPO; KP=
KPO; KP=  SSKL=
SSKL=  SP*KL=
SP*KL=  *25*20=500
*25*20=500
 №14 (11 нұсқа №25) Пирамиданың табаны-қабырғасы а-ға, сүйір бұрышы
№14 (11 нұсқа №25) Пирамиданың табаны-қабырғасы а-ға, сүйір бұрышы 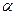 -ға тең ромб. Пирамидаға жасаушысы табан жазықтығымен
-ға тең ромб. Пирамидаға жасаушысы табан жазықтығымен 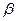 бұрыш жасайтын конус іштей сызылған. Конустың көлемін табыңыз.
бұрыш жасайтын конус іштей сызылған. Конустың көлемін табыңыз.
<A= 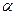 <SAO=
<SAO= 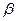 V=
V=  Sтаб *SO
Sтаб *SO 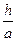 =sin
=sin 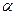 h=a sin
h=a sin 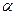 r=
r=  h=
h=  a sin
a sin 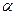
SO=  sin
sin 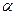 tg
tg 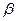 Sтаб=
Sтаб=  r2=
r2=  (
( a sin
a sin 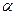 )2
)2
V=  *(
*( )2a2sin2
)2a2sin2 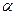 *
*  sin
sin 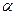 tg
tg 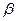 =
= 
 sin3
sin3 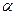 tg
tg 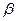
№15 (16 нұсқа №25) Конустың биіктігі 3  см, табанының радиусы 5 см.
см, табанының радиусы 5 см.
Төбесі арқылы өтетін биіктігімен 300жасайтын қиманың ауданын табыңыз.
 SO=3
SO=3  см R=5 см. <PSO=300 SSKL=
см R=5 см. <PSO=300 SSKL=  KL*SP SP=2PO
KL*SP SP=2PO
SP=2x, PO=x SO2=SP2-PO2 3x2=27 X2=9 X=3
SP=6, PO=3 KP=  =4 KL=2KP=8
=4 KL=2KP=8
SSKL=  KL*SP=
KL*SP=  *8*6=24 см2
*8*6=24 см2
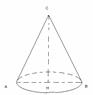 №16 (19 нұсқа №25) Конустың биіктігі 4
№16 (19 нұсқа №25) Конустың биіктігі 4  см. Конус бүйір бетінің жазбасының центрлік бұрышы 1200.Конустың көлемін табыңыз. CH=4
см. Конус бүйір бетінің жазбасының центрлік бұрышы 1200.Конустың көлемін табыңыз. CH=4 
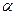 =
= 
 L=3R H=
L=3R H=  H=2R
H=2R  2R
2R  =4
=4  R=2
R=2
V=  R2H V=
R2H V=  *22*4
*22*4  =
= 
 №17 (21 нұсқа №24) Конустың бүйір бетінің ауданы табанының ауданынан 2 есе артық болса, жазбасының бұрышын радианмен табыңыз.
№17 (21 нұсқа №24) Конустың бүйір бетінің ауданы табанының ауданынан 2 есе артық болса, жазбасының бұрышын радианмен табыңыз.
Sб.б=  RL
RL
Sб.б=2Sтаб
 RL=2
RL=2  R2
R2
L=2R 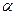 =
= 
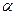 =1800
=1800
№ 18 (16 нұсқа №25) Конустың көлемі V –ға тең. Конусқа іштей сызылған дұрыс төртбұрышты пирамиданың көлемін табыңыз. V=  R2H H=
R2H H=  Vпир=
Vпир=  Sтаб*H
Sтаб*H
R-төртбұрышқа сырттай сызылған шеңбердің радиусы
a-төртбұрыштың қабырғасы a=  R Sтаб=a2=(
R Sтаб=a2=( R)2=2R2
R)2=2R2
Vпир =  Sтаб*H=
Sтаб*H=  *2R2*H=
*2R2*H=  *2R2*
*2R2*  =
= 
№19 (17 нұсқа №25) Радиусы 6 см-ге тең жарты дөңгелек конусқа айналдырылған. Кoнустың көлемі неге тең? С=  R=6
R=6  H=
H=  H=
H= 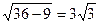
C=2  R 2
R 2  R=6
R=6  R=3 V=
R=3 V=  R2H=
R2H=  *9*3
*9*3  =9
=9 

 №20 (20 нұсқа №18) Конустың осьтік қимасы тік бұрышты үшбұрыш.P=16(2+
№20 (20 нұсқа №18) Конустың осьтік қимасы тік бұрышты үшбұрыш.P=16(2+  ), толық бетінің ауданы неге тең? AC=BC=L, AB=2R AC2+BC2=AB2 2L2=4R2 L=
), толық бетінің ауданы неге тең? AC=BC=L, AB=2R AC2+BC2=AB2 2L2=4R2 L=  R P=2R+2L 2R+2L=16(2+
R P=2R+2L 2R+2L=16(2+  ) R+L=8(2+
) R+L=8(2+  )
)
R+  R=8(2+
R=8(2+  ) R(1+
) R(1+  )=8
)=8  (1+
(1+  ) R=8
) R=8 
L=  *8
*8  =16
=16
Sт.б=  R(R+L)=
R(R+L)=  *8
*8  *(8
*(8  +16)=
+16)=  *8
*8  *8
*8  (1+
(1+  )=128
)=128  (1+
(1+  )
)
 №21 (2003ж. 2 нұсқа №27) Қиық конустың табан радиусы 7 м және 4 м. Жасаушысы табанына 600бұрышпен көлбеген.Жасаушысын табыңыз. OC=4 м.
№21 (2003ж. 2 нұсқа №27) Қиық конустың табан радиусы 7 м және 4 м. Жасаушысы табанына 600бұрышпен көлбеген.Жасаушысын табыңыз. OC=4 м.
ND=7 м <D=600 DC-? DH=DN-HN=7-4=3м  =cos600
=cos600
DC=3:  =6м
=6м
№22 (18 нұсқа №11) Қиық конустың табанының диаметрі 3м, 6м, биіктігі 4 м. Жасаушысын табыңыз. AD=6, BC=3, CH=4, DC-? HD=  (AD-BC)=
(AD-BC)=  *(6-3)=1,5
*(6-3)=1,5
DC2=CH2+HD2 DC2=16+2,25=18,25 DC= 
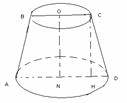 №23 (23 нұсқа №26) Қиық конустың табанының радиустары 10 см және 4 см, ал жасаушысы табан жазықтығына 450 бұрыш жасай көлбеген. Конустың осьтік қимасының ауданын табыңыз. ND=10, OC=4, <D=450 SABCD-?
№23 (23 нұсқа №26) Қиық конустың табанының радиустары 10 см және 4 см, ал жасаушысы табан жазықтығына 450 бұрыш жасай көлбеген. Конустың осьтік қимасының ауданын табыңыз. ND=10, OC=4, <D=450 SABCD-?
HD=ND-OC=10-4=6 HD=CH=6
S=  (AD+BC) *CH=
(AD+BC) *CH=  (20+8)*6=84
(20+8)*6=84
№24 (2009ж 10 нұсқа №25) Конустың көлемі 375 см3. Биіктігі 5 см.Конус төбесінен 2 см қашықтықтан өтетін және де оның табанына параллель жазықтық қияды. Пайда болған қиық конустың көлемін табыңыз.
 V=375 см3 H=5 см. SC=2cм Vқиық кон-?
V=375 см3 H=5 см. SC=2cм Vқиық кон-?
V=  R2H
R2H  R2*5=375 R2=225:
R2*5=375 R2=225:  R=
R=  CN=x
CN=x
 x=
x= 
V=  H(r2+R2+R*r)=
H(r2+R2+R*r)=  *3*(
*3*( )=351 см2
)=351 см2
Мазмұны:
І бөлім Жазықтықтардың қасиеттері
ІІ бөлім. Пирамида
ІІІ бөлім Параллелепипед
ІҮ бөлім Куб
Ү бөлім Призма
ҮІ бөлім Шар
ҮІІ бөлім Цилиндр
ҮІІІ бөлім Конус
Date: 2015-12-10; view: 9513; Нарушение авторских прав