І бөлім Жазықтықтардың қасиеттері 4 page

AB=10, BC=17, AC=21, L-бүйір қыры, L=18 p=

S=

V=S_ABC*L, L-бүйір қыры

V=84*18=1512cм³
2007 ж №9 (5 нұсқа №24) Дұрыс төртбұрышты призманың диогоналі мен бүйір жағының арасындағы бұрыш 30⁰, ал табанының қабырғасы а-ға тең. Призманың көлемін табыңыз. <TAM=30⁰, AB=a V-? TM=a, MA=2a MA²=a²+a²+h²

h²=4a²-2a²=2a² h= a S_ABC=a² V= S_ABC*h=a²* a= a³

№10 (11 нұсқа №14)Төртбұрышты дұрыс призманың диогоналі бүйір жағымен 30⁰ бұрыш жасап көлбейді. Диогоналінің табан жазықтығымен жасайтын бұрышын табыңыз.

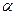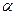<TAM=30⁰, AB=a V-? TM=a, AM=2a AC= a cos = =45⁰

№11 (15 нұсқа №24)Үшбұрышты дұрыс призманың табан қабырғасы мен оған қарсы жатқан қырының ортасы арқылы өтетін жазықтық табан жазықтығымен 45⁰ бұрыш жасайды.Табан қабырғасы а-ға тең болса, призманың бүйір бетінің ауданын табыңыз. AB=a, <KOC=45⁰ S_б.б-? OC²=BC²-OB²

OC= =tg45⁰ KC= H=2* =a

P=3a S_б.б=PH=3a* a =3 a³

2009ж №12 (2 нұсқа №18)Тік призманың табанында жатқан үшбұрыштың бір қабырғасы 2м, ал қалғандары 3м-ге тең. Призманың бүйір қыры 4м. Осы призмамен көлемдері бірдей кубтың қырын табыңыз. AB=2м, AC=BC=3м, AM=4м, V_призма=V_куб P=

S= V_призма=SH=2 *4=8 V_куб=a³ a³=8 a=2

2010 ж №13 (11 нұсқа №9)А(2;0;0), В(0;0;0), С(0;2;0) В₁(0;0;2) АВСА₁В₁С₁ призманың төбелері болса, С₁ нүктесінің координатасын табыңыз.C₁(0;2;2)
№14 (11 нұсқа №25) Дұрыс төртбұрышты призманың табанының диогоналі 4 см, бүйір жағының диогоналі 5см. Осы призмаға іштей сызылған цилиндрдің бүйір бетінің ауданын табыңыз. AC=4 см AT=5 см Sб.б-цилиндр-? Sб.б=2 RH AC²=AB²+BC² 2AB²=32 AB²=16 AB=4 AP²=AT²-PT²=25-16=9

AP=3 см R=AC:2=4 :2=2

Sб.б=2 RH=2 *2 *3=12 см²

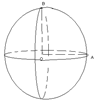ҮІ бөлім ШарЖарты дөңгелек өзін шектейтін диаметрден айналғанда шығатын фигураны шар деп атайды.

V= R³

S=4 R²

2003ж №1 ( 1 нұсқа №27)Шардың радиусы 8 см-ге, ал қиманың радиусы см-ге тең. Шардың центрінен қима жазықтығына дейінгі қашықтықты табыңыз.

R=OB=8 см

AB= см

AO-?

AO²=OB²-AB² AO²=64-15=49 AO=7см
№2(15 нұсқа №11)Радиусы 41 см шар центрінен 9 см қашықтықты жазықтықпен қиылған. Қиманың ауданын табыңыз.

R=OB=41 см

AO=9 см

AB²=OB²-AO²

AB²=1681-81=1600 S= R² S=1600

№3 (17 нұсқа №27)Шар бетінің ауданы 36 . Шардың көлемін табыңыз. S=4 R²

36 =4 R² R=3 V= R³= *3³=36

№4 (29 нұсқа №11)Үш шардың радиустары 3см, 4см, 5 см. Көлемі осы шарлардың көлемдерінің арифметикалық ортасына тең болатын шардың радиусы неге тең?

R₁=3см, V₁= R₁³= *3³=36 R₂=4см, V₂= R₂³= *4³=

R₃=5 см, V₃= R₃³= *5³= V= (V₁+V₂+V₃)= (36 + + )= *288 =96

V= R³ R³= R=

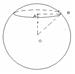2004ж №5( 15 нұсқа №30)Радиусы 17 см болып келетін шар оның центрінен 15см қашықтықта жазықтықпен қиылысады. Қима ауданын табыңыз.

R=OB=17 см

AO=15 см

AB²=OB²-AO² AB²=289-225=64 S= R² S=64

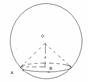№6(20 нұсқа №30) Шар секторының табанындағы шеңбердің радиусы см-ге, ал шардың радиусы 3см-ге тең. Шар секторының көлемін табыңыз.

R=OA= 3см AB= см BO²=OA²-AB² BO²=9-5=4 BO=d=2cм

H=R-d=3-2=1cм V= 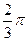R²H= 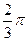*9*1=6
№7 (22 нұсқа №30)Шар бетінің ауданы 100 . Шардың көлемін табыңыз. S=4 R²

100 =4 R² R=5 V= R³= *5³=

№8 (32 нұсқа №30)Шар бетіне тиісті C, D және Е нүктелері берілген және CD=7 cм, DE=8cм, CE=9 cм. Шардың центрінен CDE үшбұрыш жазықтығының центріне дейінгі қашықтық 1 см-ге тең болса, шар бетінің ауданын табыңыз. AO=1cм, P= (7+8+9)=12 S= R_CDE= 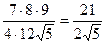OE²=AO²+AE² OE= S=4 R²S=4 * 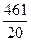=92,2

2005 ж №9 (9нұсқа №28)Бір шар бетінің ауданы 18см²-қа тең. Көлемі берілген шар көлемінен 8 есе үлкен екінші шар бетінің ауданын табыңыз. S₁=18 см² 4 R²=18 R²= R= V₁= R³= *( )³= V=V₁*8= *8= = R³ R= S=4 R² S=4 * =72cм²

№10(28 нұсқа№30)V= cм³тең болатын шар конусқа іштей сызылған.Конустың биіктігі 3 см болса, көлемін табыңыз. V= R³ R³= R_шар=1 SO=H

L-жасаушысы L²=H²+R² L= R_шар= =1 3R=R+ =2R 4R²=9+R² R²=3 S_конус= R² S_конус=3 V= S_конусH= *3 *3=3

№11 (29 нұсқа №30) Шарлардың радиустары 25 дм, 29 дм, ал олардың центрлерінің ара қашықтығы 36 дм.Шарлардың беттерінің қиылысу сызығының ұзындығын табыңыз.

AB=25 дм, BC=29 дм, AC=36 дм AD=x , DC=36-x BD²=AB²-AD²

BD²=BC²-DC² 25²-x²=29²-(36-x)² 625- x²=841-1296+72x- x² 72x=1080

x=15 BD²=AB²-AD² BD²=625-225=400 BD=20

C=2 R=2 *20=40 дм=4 м

2006 ж №12(26 нұсқа №14)Шардың көлемінің және оның беттерінің аудандарының сан мәндері тең. Шардың радиусын табыңыз. V_шар= S_б.б R³=4 R² R=3 cм

2007ж №13( 2 нұсқа №30) Сыртқы диаметрі 10,7 см, ал ішкі диаметрі 8,6 см-ге тең іші қуыс шойын шардың массасын есептеп шығарыңдар. Шойын тығыздығы 7,3г/см³

AB=10,7 см CD=8,6 см =7,3 г/см³ m= V

R₁=AB/2=10,7:2=5,35 V₁= R₁³= *5,35³=204,17

R₂=CD/2=8,6:2=4,3 V₂= R₂³= *4,3³=106,009

V=V₁-V₂=204,17 -106,009 =98,161 m= V m=7,3*98,161 =716,6

№14(6 нұсқа №14) Шардың көлемі 288 см³. Шар бетінің ауданын табу керек.

V=288 см³ R³=288 R=6 S=4 R²=4 *6²=144

2009ж №15(9 нұсқа №18)Шарды қиятын екі параллель жазықтық шар центрінің екі жағында орналасқан. Қималардың аудандары 144 және 25 . Жазықтықтардың арасы 17 см болса, шар бетінің ауданын табу керек.

AB=17см S₁=144 S₂=25 S_шар-? R₁²=144 BC=R₁=12

R₂²=25 AD=R₂=5 AO=x, BO=17-x CO²=BO²+BC² DO²=AO²+AD²

DO=CO=R (17-x)²+144=x²+25 289-34x+x²+144= x²+25 34x=408

X=12 AO=12, DO²=144+25=169 DO=13 S=4 *R²=676

№16 (18 нұсқа №24) Шардың өзара перпендикуляр екі қимасының ортақ хордасының ұзындығы 12 см. Қималардың аудандары 100 және 64 болса, шардың радиусын табыңыз. S₁=100 R₁=10 S₂=64 R₂=8 AB=12 см. AKD; KD²=AD²-AK² KD²=100-36=64 KD=8 BKC KC²=BC²-KB²

KC²=64-36=28 KC=2 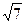DKO; KO²=KD²+DO² KO²=64+28=92

AKO AO²=AK²+KO² AO²=36+92=128 R=

2010ж №17 (15 нұсқа №25)Сфера центрінің бір жағында орналасқан, сфераны қиятын параллель жазықтықтардың қималарының ұзындығы 10 және 24 . Жазықтықтардың арасы 7 см болса, сфера бетінің ауданын табыңыз. AB=7, C₁=10 , C₂=24 . S_сфера-? 2 R₁=10 AC=R₁=5 2 R₂=24 . BD=R₂=12 AOC; BO=x AO=x+7 OC²=AO²+AC²=(x+7)²+25 BOD OD²=BO²+BD²=x²+144 OC=OD=R (x+7)²+25= x²+144 X²+14x+49+25=x²+144 14x=70 X=5 R²= x²+144=25+144=169 R=13 S=4 *R²=4 *169=676

ҮІІ бөлім Цилиндр Цилиндрдеп тік төртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын фигураны айтады. V= R²H S_б.б=2 RH S_т.б= S_б.б+2S_таб

2003ж №1 (7 нұсқа №21) Биіктігі 3см-ге тең, ал осьтік қимасы шаршы болатын цилиндрдің бүйір бетінің ауданын табыңыз. AC=H=3см R=AB:2=3:2=1,5 см S=2 RH

S=2 *1,5*3=9

№2 (13 нұсқа №11)Цилиндр биіктігі 2 м, табан радиусы 3 см. Көлемін табыңыз.

H=2 м=200 см. R=3 см. V= R²H V= *3²*200=1800 см³

№3 (14 нұсқа №11)Цилиндрдің биіктігі 6 дм, ал табанының радиусы 5дм. Цилиндрдің бүйір бетінің ауданын табыңыз. H=6 дм, R=5дм. S=2 RH S=2 *5*6=60 дм²

№4 (16 нұсқа №11)Цилиндрдің осьтік қимасының ауданы 24 см². Бүйір бетінің ауданын табыңыз. S_ABCD=24 см², S_б.б=2 RH AB=2R AC=H S_ABCD=AB*AC S_б.б=24 см²

№5 (16 нұсқа №27)Осьтік қимасының ауданы 30см², ал табанының ауданы 9 см² цилиндр берілген. Көлемін табыңыз. S_ABCD=30 см², Sтаб=9 см² Sтаб= R² R²=9