Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Повний диференціал, його застосування
|
|
Для функції Z = f (x, y) повний приріст у точці М (x, y) означається як
DZ = f (x + Dx, y + Dy) – f (x, y).
Неперервність функції Z = f (x, y) у точці М (x, y) можемо означити так:
А тепер перейдемо до виведення формули для DZ, яка в подальшому гратиме важливу роль.
Перетворимо вираз для повного приросту функції, застосовуючи відому формулу Лагранжа для однієї змінної: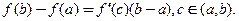 
В результаті отримаємо:
DZ = f(x + Dx, y + Dy) – f (x, y) = (f (x + Dx, y + Dy) – f (x, y + Dy)) +
+ (f (x, y + Dy) - f (x, y)) =
= 
Dx + 
Dy,
де x < c1 < x + Dx; y < c2 < y + Dy, якщо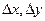 
> 0, якщо ж
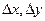< 0, то матимемо протилежні нерівності.
Нехай в точці М (x, y) обидві частинні похідні неперервні.
Оскільки 
неперервна, тобто
,
то із властивості границі випливає, що в околі точки М(x, y) має місце співвідношення:
,
де 
Аналогічний вираз маємо для
: 
,
де 
Таким чином, отримуємо формулу повного приросту функції двох змінних:
, (5.1)
де e1,e2 ® 0, якщо Dx, Dу ® 0.
Означення 5.1. Функція називається диференційовною в точці М(x, y), якщо в деякому околі цієї точки DZ має вигляд (5.1).
Означення 5.2. Диференціалом функції Z= f(x, y) називається головна частина її приросту, лінійна щодо приросту її аргументів:
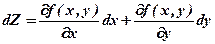, (5.2)
де dx = Dx, dy = Dу, бо приріст незалежної змінної дорівнює її диференціалу.
Доданки в (5.2) є частинними диференціалами:
dxZ = 
, dyZ = 
.
Зазначимо, що на відміну від функції однієї змінної, диференційовність функції двох змінних передбачає не тільки існування й обмеженість частинних похідних, а й їх неперервність.
Для функції Z = f (x1 , x2 , …, xn) маємо:
dZ = 
.
Приклади. Знайти повні диференціали функції:
1. 
. 2. 
. 3. 
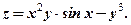4. 
.
Розв’язання. 1. . За формулою (5.2) маємо:
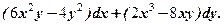
2. . 
.
3. 
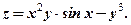
4. 
. 
Застосування повного диференціала базується на наближеній рівності:
.
Нехай відомо значення f (x0 ,y0 ). Тоді для 
маємо формулу для наближеного обчислення:
.
Звідки отримуємо формулу для наближеного значення функції:
(5.3)
Приклад. Обчислити наближене значення функції 
в точці М1(2,05; 2,94).
Представимо 2,05=2+0,05; 2,94=3-0,06. Тоді:
Легко бачити, що
.
Обчислимо значення диференціала функції 
в точці М0(2,3):
= 
.
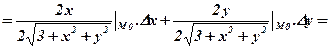
Згідно формули (5.3) знаходимо:
.
Більш точний результат за допомогою мікрокалькулятора дає 3,9807.
Якщо Z=f (x,y), то похибка DZ при обчисленні Z за умови, що х і у виміряні з похибками Dх і Dу, має вигляд:
-
- формула для оцінки абсолютної похибки наближених обчислень.
Date: 2015-12-10; view: 663; Нарушение авторских прав