Лінії та поверхні рівня

Означення 2.1. Змінна величина Z називається функцією двох змінних x і y, якщо кожній парі чисел (x, y) (або кожній точці М(x, y)) з деякої множини D площини xOy ставиться у відповідність визначене значення змінної Z. Позначається

Z = f(x, y) або Z = f (M).

Наприклад.

1) Площа прямокутника S = xy є функцією двох змінних x і y – довжин відповідних сторін;

2) Об'єм конуса V = 1/3 p R²h – функція радіуса основи R і висоти h.

Означення 2.1. узагальнюється на більшу кількість змінних.

Означення 2.2. Змінна Z називається функцією незалежних змінних x₁, x₂ , … x_n з деякої множини D, що належить n -вимірному простору Rⁿ, якщо кожній точці М(x₁, x₂ , … x_n) D ставиться у відповідність визначене значення змінної Z:

Z = f (M) = f (x₁, x₂ , … x_n).

Наприклад:

1) Температура Т в даній точці М залежить від її координат x, y, z, а також від моменту часу t, в який вона вимірюється, тобто

T = f (x, y, z, t).

2) Очікуваний прибуток Р від споруджуваного промислового об'єкта є функцією затрат на його будівництво, часу t від початку будівництва до початку випуску продукції, від величини попиту Q на цю продукцію та інших економічних факторів.

Означення 2.3. Множина D точок, в яких функція визначена називається областю визначення або областю існування функції, а множина Е, яка складається із значень функції, називається множиною значень функції f (M).

У випадку n = 2 функція двох змінних Z = f (x, y) може розглядатися як функція точки площини в тривимірному просторі R³.

Графіком функції Z = f (x, y) є геометричне місце точок (x, y,) f (x, y)), яке описує деяку поверхню в просторі R³.

Приклад 2.1. Знайти область визначення і множину значень функції

.

Функція Z має дійсні значення за умови 1 – x² – y² ≥ 0, або x² + y² < 1, тобто областю визначення даної функції є замкнений круг радіуса 1 з центром в точці О(0,0). Множиною значень функції є сегмент [ 0, 1 ], що випливає з виразу Z = Ö 1 – x² – y². Графіком функції є верхня напівсфера радіуса 1 з центром в точці О(0,0,0).

Рис 2.1

Приклад 2.2. Знайти область визначення поданих функцій:

1) ;

2) ;

3) ;

4).

1). Розв’язання для виконаємо за такою схемою:

1. Нагадаємо, що елементарна функція визначена, якщо .

2. Складаємо аналогічну нерівність для заданої функції двох змінних: , яка рівносильна двом системам нерівностей, а саме,

(1) , або (2) .

3. Замінимо останні нерівності рівняннями, отримаємо рівняння границі області визначення: х=2 – пряма, перпендикулярна осі ОХ, у=1 – пряма, перпендикулярна осі ОУ. Будуємо їх в системі ХОУ (див. рис. 2.2)

4. Відносно прямих х=2 і у=-1 вибираємо ті частини площини ХОУ, де виконуються нерівності (1) або (2).

Рис. 2.2.

2). Розв’язання для функції , проведемо за викладеною вже схемою:

1. Елементарна функція однієї змінної y=lg x визначена, якщо x>0.

2. Аналогічна нерівність для функції запишеться:

. (3)

3. Замінимо в (3) нерівність рівнянням: 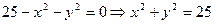- коло радіуса 5 з центром в О(0;0), яке є границею області.

4. Пробна точка О(0;0) задовольняє нерівність (3)

Отже, О(0;0) належить області розв’язків нерівності (3). Тобто вся область визначення – це множина точок, які лежать у середині заданого круга, виключаючи границю , бо нерівність (3) строга (див. рис. 2.3).

Рис 2.3

3) Розв’язання для функції за відомою схемою:

1. Відповідною елементарною функцією однієї змінної є , яка існує для .

2. Аналогічна нерівність для функції запишеться:

. (4)

3. Замінивши нерівності на рівняння, отримаємо дві параболи і , які симетричні відносно осі ОУ з вітками напрямленими вверх, причому вершина першої з них в точці , а другої в точці .

4. Пробна точка О(0,0) задовольняє ліву а також і праву нерівності (4)

,

Тобто початок координат знаходиться нижче першої параболи і вище другої - . Область визначення - всі точки площини ХОУ між цими параболами, включаючи і ці криві (див. рис. 2.4).

Рис. 2.4

4) Розв’язання для функції .

1. Відповідна функція однієї змінної 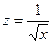визначена для .

2. Для функції аналогічна нерівність запишеться:

. (5)

3. Рівняння описує еліпс, канонічна форма якого:

, (6)

півосі цього еліпса , .

4. Пробна точка О(0,0) нерівність (5) не задовольняє, бо нерівність - невірна, тобто О(0,0), як внутрішня точка даної фігури, не входить у множину розв’язків нерівності (5). Множина розв’язків нерівності (5) – це всі точки, які лежать зовні еліпса. (див. рис. 2.4), не включаючи точок еліпса.

Рис 2.5

Приклади для самостійного розв’язання:

Знайти область визначення функції:

1. 2. 3.

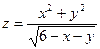4. 5. 6.

Відповіді. 1. Множина точок, які розміщені між віссю ОУ вище вітки параболи в першій чверті. 2. Множина точок .

3. Множина точок . 4. Множина точок , які розміщені на еліпсі та зовні його. 5. Множина точок , які розміщені строго нижче прямої . 6. Областью визначення є смуга між двома паралельними прямими і , включно з цими прямими.

Означення 2.4. Лінією рівня функції Z = f (x, y) називається лінія f (x, y) = С на площині xOy, в точках якої функція має стале значення Z = C.

Означення 2.5. Поверхнею рівня функції U = f (x, y, z) називається поверхня f (x, y, z) = С, в точках якої функція має стале значення U = C.

Приклад 2.3. Знайти лінії рівня функції

Рівняння ліній рівня 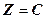мають вигляд

(C > 0). Якщо С приймає дійсні значення, то отримуємо концентричні кола з центром в точці О(0,0), радіуса , де ..

Зауважимо, що за допомогою ліній рівня f (x, y) = С можна побудувати поверхню Z = f (x, y) (рис. 2.2)

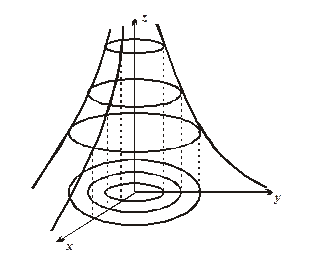
Рис. 2.6.

Основними способами задання функції двох змінних є такі:

1) аналітичний, тобто за допомогою аналітичного виразу(формули);

2) табличний, за допомогою таблиці з двома входами, де кожній парі чисел та 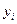ставиться в таблиці відповідне значення

3) графічний, графіком функції двох змінних може бути деяка поверхня

Date: 2015-12-10; view: 1091; Нарушение авторских прав