
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бинарные отношения. Разбиение множества
|
|
Между элементами множества могут быть установлены некоторые отношения, при этом указывается, какие элементы этого множества, взятые в определенномпорядке, состоят в данном отношении, а какие – нет. Например, во множестве R действительных чисел можно ввести следующее отношение  . Очевидно, что это отношение определяется как подмножество прямого произведения R
. Очевидно, что это отношение определяется как подмножество прямого произведения R  R, т.е.
R, т.е.
 .
.
Бинарным отношением  на множестве A называется всякое подмножество
на множестве A называется всякое подмножество  . Если
. Если  , то пишут
, то пишут  .
.
Аналогично определяется n -парное отношение  на множестве А:
на множестве А: 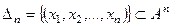
Рассмотрим некоторые важные свойства бинарных отношений:
отношение  на A называется рефлексивным, если
на A называется рефлексивным, если
 .
.
Отношение  на A называется симметричным, если
на A называется симметричным, если
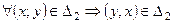 .
.
Отношение  - транзитивно, если
- транзитивно, если
 и
и  .
.
Симметричное, рефлексивное и транзитивное отношение называется отношением эквивалентности. Для обозначения отношения эквивалентности используют знак ~.
Пример. Отношение  на множестве R являются отношением эквивалентности, что очевидно:
на множестве R являются отношением эквивалентности, что очевидно:
1)  ,
,
2) если  ,
,
3) если  , то
, то  .
.
Отношение эквивалентности на произвольном множестве связано с понятием разбиения этого множества. Разбиение множества A на подмножества (классы)  называется представлением A в виде объединения непересекающихся подмножеств
называется представлением A в виде объединения непересекающихся подмножеств  .
.
Пусть 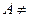 Æ разбито на классы
Æ разбито на классы  . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение  на множестве
на множестве  лишь тогда и только тогда, когда элементы x и y принадлежат одному классу
лишь тогда и только тогда, когда элементы x и y принадлежат одному классу  .
.
Проверкой нетрудно убедиться, что введенное отношение является отношением эквивалентности. Таким образом, всякое разбиение множества определяет некоторое отношение эквивалентности на этом множестве. Верно и обратное.
Теорема. Всякое отношение эквивалентности ~ на множестве A определяет разбиение множества A на  классы эквивалентности.
классы эквивалентности.
Действительно, каждому  сопоставим
сопоставим 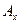 ={ у, где
={ у, где  ~
~  }. Тогда:
}. Тогда:
1) каждый класс  Æ, т.к. x~x,
Æ, т.к. x~x,
2) если  и
и  , то
, то  ~
~  , что очевидно:
, что очевидно:  ~
~  ,
,  ~
~  , т.е.
, т.е.  ~
~  , то в силу транзитивности
, то в силу транзитивности  ~
~  ,
,
3) если 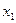 ~
~  , то
, то  . Действительно:
. Действительно:  ~
~ 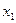 , где
, где  ~
~ 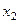 , то
, то  ~
~  , т.е.
, т.е.  , аналогично
, аналогично  . Значит
. Значит  .
.
4) элементы разных классов не эквивалентны, что очевидно по пункту 3,
5) разные классы не пересекаются, что очевидно, в противном случае не выполнялся бы пункт 4.
Таким образом, A есть объединение всех классов. Новое множество, состоящее из полученных классов, называется факторпространством.
Date: 2015-12-10; view: 451; Нарушение авторских прав