
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Высказывания и кванторы
|
|
В математике обычно используются предложения, которые содержат определенные утверждения с использованием некоторой переменной (переменных): например, «натуральное число x, такое, что 2x-3x2 >0» и др. Истинность таких предложений зависит от значения переменной (переменных). Такие предложения называются неопределенными высказываниями (предикатами), их обозначают символами  и т.д.
и т.д.
Придавая переменным различные значения из указанного множества, получаем из неопределенных высказываний различные высказывания: истинные, ложные.
Множеством истинности неопределенного высказывания  называется множество всех значений x, при которых предикат
называется множество всех значений x, при которых предикат  обращается в истинное высказывание.
обращается в истинное высказывание.
Два неопределенных высказывания, заданные на одном и том же множестве, называются равносильными, если множества их истинности совпадают.
Из неопределенного высказывания можно получить высказывания и другим способом – с использованием кванторов.
Кванторы – это логические операции. Наиболее употребительны два квантора: квантор общности  (читают: для всех, для любых) и квантор существования
(читают: для всех, для любых) и квантор существования  (читают: существует, для некоторого). Кванторы
(читают: существует, для некоторого). Кванторы  ,
,  определяют множество истинности неопределенного высказывания. Например, если некоторое неопределенное высказывание
определяют множество истинности неопределенного высказывания. Например, если некоторое неопределенное высказывание  верно при любом значении х из множества М, то пишут:
верно при любом значении х из множества М, то пишут:  . Если же высказывание
. Если же высказывание  истинно хотя бы для одного элемента х из множества М, то применяют квантор существования
истинно хотя бы для одного элемента х из множества М, то применяют квантор существования  , записывают так:
, записывают так:  .
.
Применение кванторов к неопределенным высказываниям иногда называют «навешиванием кванторов». Навешивание кванторов на неопределенные высказывания может обращать их как в истинные, так и в ложные высказывания.
В математике часто из одних утверждений получают другие утверждения с использованием следующих логических операций (при этом условимся истинность утверждения обозначать значением 1, а ложность - значением 0):
1.Операция отрицания
Отрицанием утверждения A называется утверждение, обозначаемое  , которое истинно, если A-ложно, и наоборот, т.е.
, которое истинно, если A-ложно, и наоборот, т.е.
| A | 
|
2.Операция дизъюнкции
Дизъюнкцией утверждений A и B называется утверждение, обозначаемое A  B, которое истинно, если истинно хотя бы одно из утверждений A или B, т.е.
B, которое истинно, если истинно хотя бы одно из утверждений A или B, т.е.
| A | B | A  B B
|
3.Операция конъюнкции
Конъюнкцией утверждений A и B называется утверждение, обозначаемое A 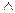 B, которое истинно, если истинны оба утверждения, и ложно в противном случае
B, которое истинно, если истинны оба утверждения, и ложно в противном случае
| A | B | A 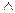 B B
|
4.Операция импликации („если А, то В”) A→B
Импликацией от утверждения A к утверждению B называется утверждение, которое ложно лишь тогда, когда A – истинно и B –ложно, т.е.
| A | B | A→B |
Высказывание А называется посылкой высказывания В, а высказывание В– его заключением.
5.Операция эквиваленции
Эквиваленцией высказываний A и B называется высказывание, которое истинно лишь тогда, когда A и B истинны или ложны одновременно, т.е.
| A | B | A↔B |
Имеется следующий порядок действий операций по старшинству: ↔, →,  ,
, 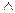 , −.
, −.
Кванторы, неопределенные высказывания и логические операции наиболее часто могут быть использованы в формулировке теорем, например, в таком виде: для каждого элемента х множества М из  следует
следует 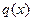 . Кратко такую теорему принято записывать так:
. Кратко такую теорему принято записывать так:
 ,
,
где  называется условием теоремы на М,
называется условием теоремы на М, 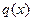 – заключением теоремы.
– заключением теоремы.
Например. Если действительное число кратно 4, то оно четно. Здесь М – множество всех действительных чисел, условие теоремы – «кратно 4», заключение – «оно четно».
Утверждения  и
и  называются взаимно обратными. Одно из них можно назвать прямым утверждением, тогда другое называют обратным.
называются взаимно обратными. Одно из них можно назвать прямым утверждением, тогда другое называют обратным.
Заметим, что для взаимно обратных утверждений могут быть следующие ситуации:
– оба утверждения верны или оба утверждения неверны,
– одно утверждение может быть верное, а другое неверное.
Пусть дана некоторая теорема  , тогда условие
, тогда условие  теоремы называют достаточным условием для заключения
теоремы называют достаточным условием для заключения 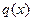 , а заключение
, а заключение 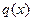 теоремы называют необходимым условием для
теоремы называют необходимым условием для  .
.
Если справедлива не только прямая, но и обратная теорема, то 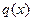 является необходимым и достаточным условием для
является необходимым и достаточным условием для  , а
, а  является необходимым и достаточным условием для
является необходимым и достаточным условием для 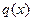 , при этом доказательство теоремы должно состоять из доказательства необходимости и доказательства достаточности.
, при этом доказательство теоремы должно состоять из доказательства необходимости и доказательства достаточности.
Например, подобная сказанному теорема: для того, чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали точкой пересечения делились пополам.
Или, по-другому: четырехугольник является параллелограммом тогда и только тогда, когда его диагонали делятся точкой пересечения пополам.
Date: 2015-12-10; view: 1421; Нарушение авторских прав