Множество. Операции над множествами

Множеством является совокупность объектов, объединенных по некоторому признаку. Эти объекты называются элементами множества. Множества обозначают большими буквами латинского алфавита, а их элементы - малыми буквами греческого и латинского алфавитов: .

Если элемент 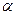принадлежит множеству А, то пишут: 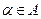или (читают: множество А содержит 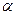), в противном случае пишут 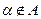(читают: элемент 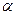не принадлежит множеству А).

Если два множества А и В состоят из одних и тех же элементов, то говорят, что они равны, и пишут А=В. Если некоторое множество А не содержит никаких элемента, то А – пустое множество, пишут 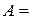Ø.

Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В, пишут или 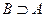; если или А=В, то пишут .

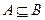Заметим, что множество может быть конечным, например, 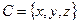, и бесконечным, например, 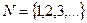– множество натуральных чисел. Два множества А и В называются эквивалентными (пишут А ~ В), если между ними установлено взаимнооднозначное соответствие (биекция), т.е. каждому элементу множества А соответствует единственный элемент множества В и, наоборот, каждому элементу множества В соответствует единственный элемент множества А.

Например, 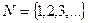– множество натуральных чисел и 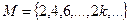– множество четных натуральных чисел, где 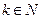– эквивалентные множества.

Операции над множествами.

Пересечение множеств . Пересечением двух множеств А и В называется новое множество , элементы которого принадлежат и множеству А, и множеству В.

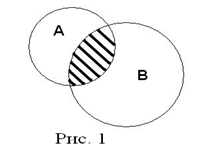Множество С на рис. 1 заштриховано.

Аналогично определяется пересечение более двух множеств: например, трех множеств: 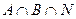(рис.2). Имеет место равенство: .

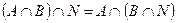Объединение множеств: 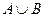. Объединением двух множеств А и В называется новое множество , элементы которого принадлежат множеству А или множеству В. Множество С на рис. 3 заштриховано. Аналогично определяется объединение более двух множеств: например, трех множеств, причем .

Разность двух множеств (вычитание): . Разностью множеств А и В называется новое множество , которое состоит из всех элементов множества А, не принадлежащих множеству В.

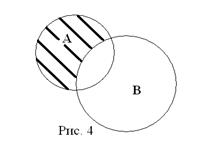Множество С на рис.4 заштриховано.

Дополнение множества А до множества В. Пусть . Дополнением множества А до множества В называется множество С, которое состоит из всех элементов множества В, не принадлежащих множеству А.

Множество С на рис.5 заштриховано.

Прямое произведение множеств. Прямым произведением множеств А и В называется множество, элементами которого являются всевозможные упорядоченные пары 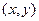, где 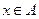, 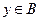. Обозначают прямое произведение так: .

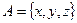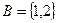Например, если и , то

.

Аналогично определяется прямое произведение более двух множеств: например, .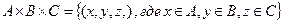

Декартово произведение 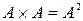называется декартовым квадратом множества А; 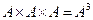– декартов куб множества А.

Декартово произведение обосновывает следующее правило произведения (комбинаторики): если объект а из множества А можно выбрать n способами, а объект b из B можно выбрать m способами, то объект а и b можно выбрать способами.

Операция объединения множеств позволяет обосновать правило суммы: если объект а из множества А можно выбрать n способами, а объект b из B можно выбрать m способами, причем каждый способ выбора объекта а отличается от любого способа выбора объекта b, то объект а или b можно выбрать 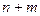способами.

Date: 2015-12-10; view: 534; Нарушение авторских прав