При кинематическом возбуждении

Решение отыскиваем в виде:

, (6.28)

которое можно представить в комплексном виде как:

, (6.29)

где ω – круговая частота;

φ – угол сдвига фаз между колебаниями основания и массы.

Определим производные и подставим их в ( 6.25):

; (6.30)

(6.31)

Тогда уравнение (6.25) приобретает следующий вид:

Или

(6.32)

Раскрывая скобки и приравнивая к нулю действительную и мнимую части с учетом того, что 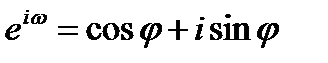, получаем:

(6.33) (6.34)

Из полученных уравнений определим z₀:

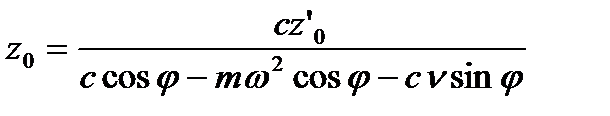; (6.35)

; (6.36)

Приравняв (6.35) и (6.36) и, произведя упрощения, получим:

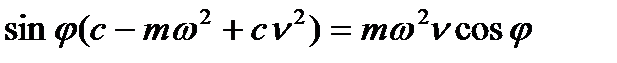. (6.37)

Откуда

, ( 6.38 )

где - угловая частота собственных колебаний.

Обозначив частотное отношение отстройки , запишем: (6.39)

На рис.6.7. приведены фазочастотные характеристики, рассчитанные по формуле (6.39).

Из рисунка видно, что при небольших значениях коэффициента потерь ν £ 0,01 фазочастотные характеристики удовлетворяют допущению В.С.Ильинского [13], что до резонанса колебания основания СВ и объекта виброзащиты происходят в «фазе», а после резонанса – в «противофазе».

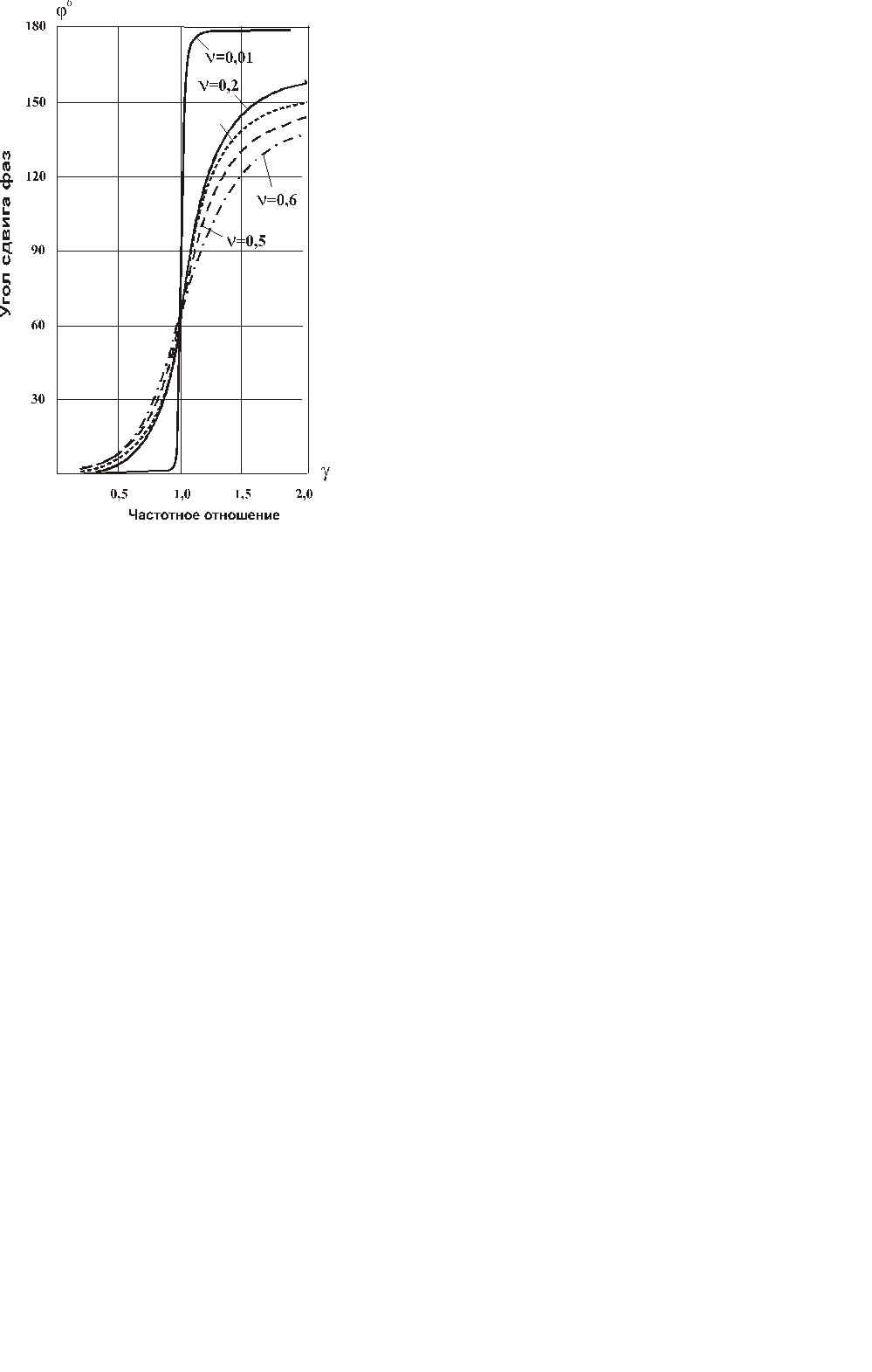
Рис. 6.7. Фазочастотная характеристика линейной системы

Однако у амортизаторов КРКВ для реальных значений ν = 0,26÷0,45 в дорезонансном диапазоне частот фазочастотные характеристики при различных величинах ν мало отличаются друг от друга, перекрывая диапазон углов фазового сдвига до 60°.

При величине отстройки γ >1,0 фазочастотные характеристики переходят в зарезонансный диапазон и изменяются в нем в среднем от 60° до 150°, не достигая противофазных значений даже при величинах частотной отстройки превосходящих единицу в 2 раза.

Анализируя фазочастотные характеристики (рис. 6.7.), рассчитанные по формуле ( 6.39 ) и фазочастотные характеристики полученные В.С.Ильинским [13] для сетчатых амортизаторов можно сделать следующие выводы:

- уже при величинах ν > 0,1 приближение В.С.Ильинского о том, что перемещение координат z ₀ и до резонанса «в фазе» а после резонанса «в противофазе» неприемлемо для КРКВ, так как угол сдвига в зависимости от величины частотной отстройки γ изменяется плавно и особенно в резонансном диапазоне, не достигая противофазного значения 180° даже при значительных величинах γ;

- кроме того, в полученном В.С.Ильинским выражении передаточной функции при вышеуказанном допущении о фазочастотных характеристиках отсутствует зависимость коэффициента вибропередачи и собственной частоты системы от коэффициента потерь ν, что неизбежно снижает точность расчетов динамических параметров системы виброизоляции.

Таким образом, для нелинейной системы снижения динамических нагрузок с амортизатором КРКВ, у которого коэффициент жесткости определяется соотношением:

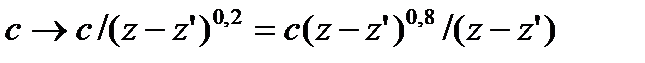, (6.40)

для значительных величин коэффициента потерь > 0,1 в нашем случае, необходимо воспользоваться другими методами решения дифференциального уравнения, например, методом гармонического баланса [2], что представлено в следующем разделе 6.4.

Date: 2015-10-21; view: 378; Нарушение авторских прав