
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кольцевых резинокордовых амортизаторов
|
|
При расчетах систем снижения динамических нагрузок вначале осуществляется расчет несущей способности, прочности и осадки амортизаторов по условию статической нагрузки весом объекта виброзащиты. Для этого необходимо знать величину коэффициента статической жесткости амортизатора в Н/м.
Рассмотрим теоретические предпосылки и установим зависимости для расчета жесткостных параметров и определение несущей способности и геометрических размеров анизотропного амортизатора.
I. Внешняя сила F вследствие действия на КРКВ пространственной внешней нагрузки может быть приложена по трем, взаимно перпендикулярным направлениям: вертикальному (растяжения-сжатия) z,горизонтальному (поперечного сдвига) y - вдоль оси цилиндрической поверхности КРКВ и горизонтальному («перекатывания») x - перпендикулярно оси y (рис.6.2 ).
2. Принимаем форму КРКВ в виде тонкостенной цилиндрической оболочки, которая под действием силы Fz - веса виброизолируемого объектапринимает эллиптическую форму (рис.6.3, а, б).
3. Материалы, составляющие КРКВ - резина и корд, имеют существенно отличающуюся жесткость - модуль продольной упругости текстильного корда примерно в 1000 раз выше, чем модуль упругости резины [1]. Поэтому деформации удлинения нитей корда практически отсутствуют.
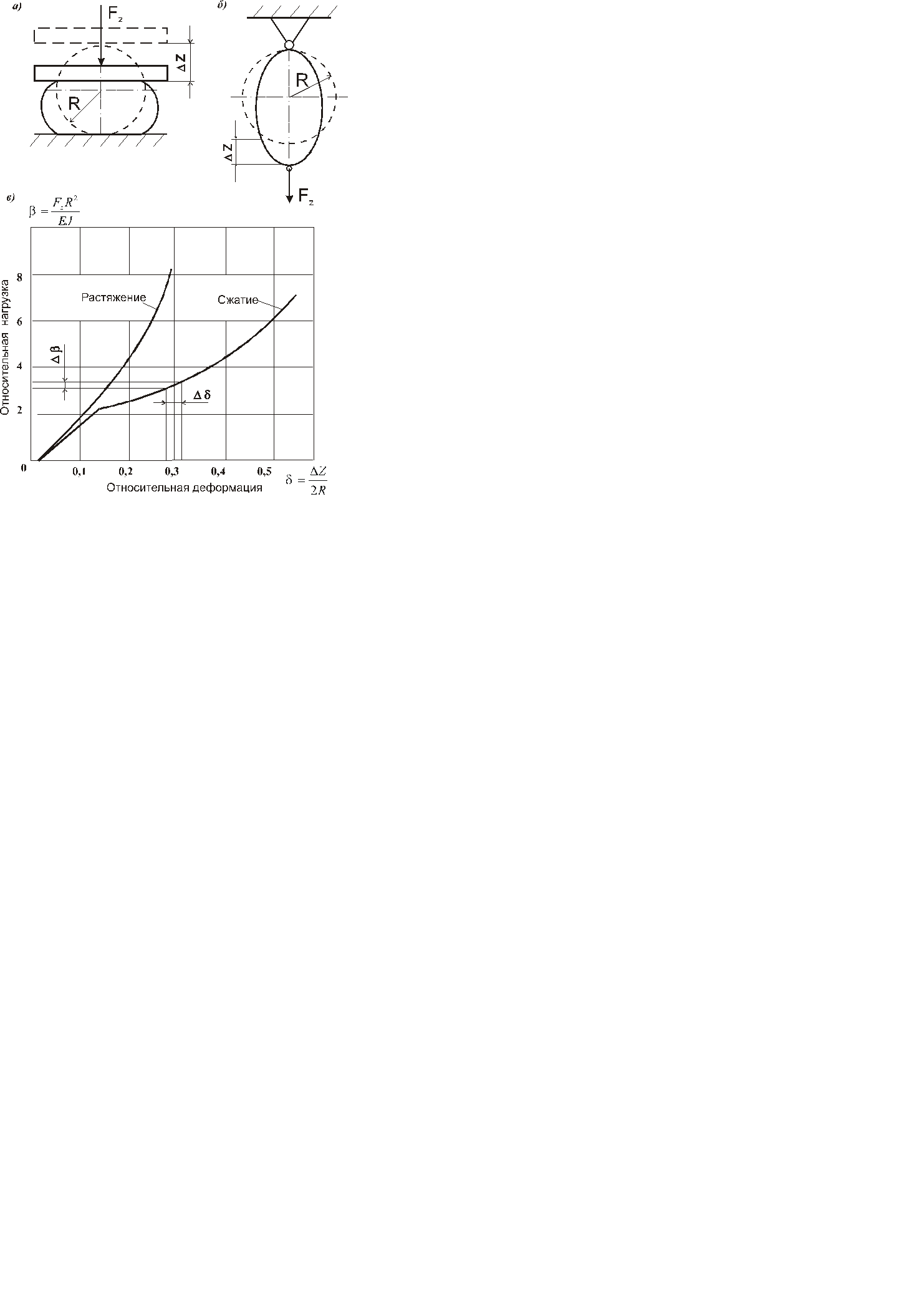
Рис. 6.3. Растяжение – сжатие кольцевых амортизаторов:
а) схема сжатия; б) схема растяжения; в) нагрузочные характеристики в относительных координатах.
4. Считаем, что деформации резины в КРКВ не превышают 10-15%. В этом случае резина подчиняется закону Гука и для расчета КРКВ, могут быть использованы обычные методы прикладной теории упругости. В этих пределах деформаций справедливы формулы расчета на растяжение, сжатие, изгиб, кручение, формулы расчета тонкостенных труб.
5. При деформации сжатия-растяжения КРКВ по оси z (рис.6.3) элементы кольца подвергаются изгибу. Из основ теории сопротивления материалов известно, что при деформации балки во время изгиба, её продольные волокна на стороне выпуклости удлиняются, а на стороне вогнутости укорачиваются. Деформация продольного волокна mn (рис.6.4, а), лежащего на расстоянии z отнейтральной поверхности:
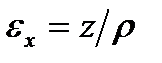 , (6.1)
, (6.1)
где ρ - радиус кривизны.
Если кольцо выполнено из однородного изотропного материала, нейтральная ось s-s, пройдет через центр тяжести сечения, как для бруса прямоугольного поперечного сеченияна высоте h/ 2, (рис.6.4, а): а) схема изгиба элемента амортизатора; б) сечение КРКВ по А-А и представление «эквивалентного» сечения из изотропного материала; в) сечение Б-Б при параллельной укладке нитей корда; г) сечение Б-Б при ромбической укладке нитей корда; д) сечение В-В корда.
Какпоказали расчеты для такой укладки кордаможно считать, что нейтральная ось s-s проходит через середину первого слоя корда от наружной поверхности кольца. Например, для случая, изображенного на рис.6.4, б, при отношении h2 / h 1 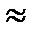 0,3 ошибка от такого предположения составила всего 0,049%.
0,3 ошибка от такого предположения составила всего 0,049%.
6. КРКВ изготавливается в виде чередующихся слоев резины и кордовых прослоек. При этом толщина hв внутреннего резинового слоя всегда больше наружного h2 для того, чтобы кордовые прослойки располагались ближе к наружной цилиндрической поверхности виброизолятора (рис.6.4, б).
7. В КРКВ может быть два варианта укладки нитей основы ткани корда - параллельно оси x (рис.6.4, б, в) или под некоторым углом к направлению оси x, так, что между собой эти нити образуют угол 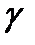 (рис.6.4, г). Рассмотрим оба случая отдельно.
(рис.6.4, г). Рассмотрим оба случая отдельно.
В первом - верхние слои корда, лежащие выше геометрической оси сечения, при изгибе должны растягиваться, а нижний резиновый – сжиматься. Но таккак модуль продольной упругости корда на три порядка выше модуля упругости резины, удлинениенитей корда практическине происходит. В этом случае мы имеем, так называемую, композитную балку. Для определения положения нейтральной оси такой балки можно пользоваться соотношением:
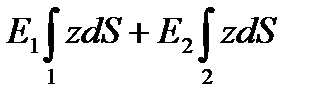 , (6.2)
, (6.2)
где Е 1 и Е2 - модули упругости материалов; S - площадь поперечного сечения материалов.
При расчетах деформации сжатия-растяжения KPKB удобно пользоваться методом приведенного поперечного сечения [9]. Балку, состоящую изразличных материалов, преобразуют в виртуальную эквивалентную балку, состоящую из одного упругого материала. Поперечное сечение такой балки, называемое приведенным – “эквивалентным” поперечным сечением, исследуется обычным способом.
Для того чтобы быть “эквивалентным” поперечному сечению исходной балки, приведенное поперечное сечение должно иметь ту же нейтральную ось и ту же способность сопротивляться изгибающему моменту. Из выражения [9]:
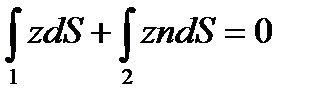 , (6.3)
, (6.3)
где n = E2 / E1 - отношение модулей упругости материалов.
Следует отметить, что положение нейтральной оси не изменится, если каждый элемент материала (например, корда) площадью dS увеличится за счет коэффициента п (в данном случае увеличивается ширина материала) при условии, что расстояние z для этого элемента останется прежним. Таким образом, получается новое (виртуальное) поперечное сечение, полностью состоящее из изотропного материала – резины. Иногда бывает удобно оставить ширину элемента неизменной, но увеличить его высоту в 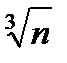 раз из условия [9]:
раз из условия [9]:
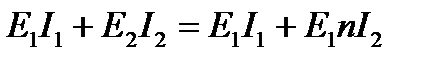 , (6.4)
, (6.4)
где I1 и I2 - моменты инерции поперечного сечения материалов относительно нейтральной оси.
В данном случае положение нейтральной оси также не изменится, а общая высота “эквивалентной” балки будет равна hэ = 2 h 1 (рис.6.4, б, изображено штриховой линией).

Рис. 6.4. К расчету жесткости растяжения-сжатия КРКВ
Во втором случае (рис.6.4, г) удлинение слоя резины происходит вследствие изменения углов γi ромбиков, образованных нитями корда. При этом модуль упругости резинокордного слоя увеличивается в К раз по сравнению с чисто резиновым [10]. Коэффициент К зависит от отношения диаметра нити корда d, к расстоянию между соседними нитями t (рис. 6.4, д) и определяется по формуле [10]:
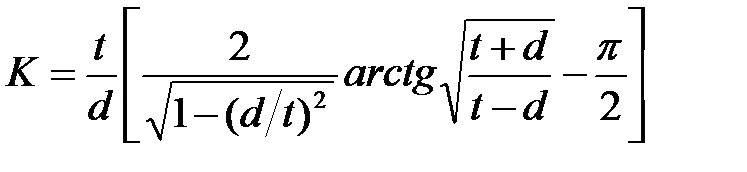 (6.5)
(6.5)
Из приведенного анализа двух вариантов укладки корда, можно отдать предпочтение первому (рис.6.4, в), так как при одинаковых геометрических размерах, КРКВ из материала с укладкой корда параллельно оси x имеет более высокую несущую способность. Кроме этого при изготовлении КРКВ из отрезков слоеной транспортерной ленты, загибаемой при сборке в кольца, такая укладка корда обеспечивает его предварительное натяжение даже без нагрузки весом объекта виброзащиты. Это наряду с повышением несущей способности амортизатора позволяет повысить трение междунитями и увеличить демпфирование.
8. Деформации сжатия-растяжения КРКВ в направлении оси z. Сжатие амортизатора под действием вертикальной силы Fz (рис.6.3, а) происходит между двумя параллельными плоскостями несущего элемента и основания. В данном случае появляется контакт по линии.
Задачу сжатия КРКВ рассматриваем как плоскую. Ввиду тонкостенности КРКВ будем считать, что энергия деформации сжатия и сдвига, по сравнению сэнергией деформации изгиба, незначительна, и поэтому ею пренебрегаем.
Нагрузочные характеристики изотропного амортизатороаиз резины [11] в безразмерных параметрах представлены на рис.6.3, в. Решение задачи в безразмерных параметрах позволяет использовать её и для определения деформации анизотропного КРКВ, зная модуль упругости применяемого материала. Это дает также возможность представления анизотропного резинокордного материала в виде эквивалентного изотропного.
Для обобщения данных по определению несущей способности KPKВ введем понятие “эквивалентный” модуль упругости – Eэ. Принимаем, что амортизатор из анизотропного материала (например, резинокорда) имеет “эквивалентный” модуль упругости, численно равный модулю упругости амортизатора из изотропного материала (например, резины). При этом полагаем, что оба амортизатора будут иметь одинаковые деформации под действием равных нагрузок, несмотря на их различные геометрические размеры.
Из выражения безразмерного параметра β (рис.6.3, в)“эквивалентный” модуль упругости представим, в виде:
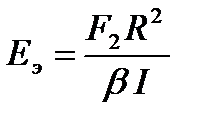 , (6.6)
, (6.6)
где I =l.h3 / 12 - момент инерции сечения КРКВ;
R - расстояние от центра недеформированного амортизатора до нейтральной оси;
l и h - соответственно ширина и высота сечения КРКВ (рис.6.4, б).
Значение β определяется по графику (рис.6.3, в) для требуемого значения относительной деформации δ. Сила Fz, соответствующая деформации δ, берется из опытных данных по статической характеристике для амортизатора изготовленного из определенного материала.
Используя график (рис.6.3, в), зная “эквивалентный” модуль упругости применяемого материала, можно определить коэффициент статической жесткости растяжения-сжатия КРКВ для любого значения относительной деформации δ:
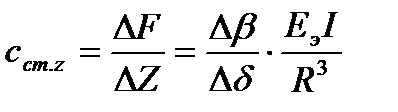 , (6.7)
, (6.7)
где значение Δ β берется для соответствующего Δ δ (рис.6.3, в), которое в свою очередь определяется измерением относительной деформации в окрестностях требуемого δ.
Основные размеры КРКВ при действии сжимающей нагрузки определяются при помощи графика, рис.6.3, в, следующим образом:
- задается величина относительной деформации виброизолятора δ поддействием силы F z (рекомендуемая величина δ  0.4);
0.4);
- по графику определяется величина β для принятой величины δ;
- используя соотношение (6.6), рассчитывается один из размеров l,h или R, задавшись двумя остальными, для действующей нагрузки на виброизолятор F z.
При растяжении КРКВ форма его деформированного состояния также изменяется, поэтому в данном случае непригодны линейные методы расчета. В  работе [119] определена зависимость деформации резинового кольца от нагрузки с учетом изменения его формы. Результаты расчетов представлены в безразмерных параметрах на рис.6.3, в.
работе [119] определена зависимость деформации резинового кольца от нагрузки с учетом изменения его формы. Результаты расчетов представлены в безразмерных параметрах на рис.6.3, в.
Основные размеры КРКВ при действии растягивающей нагрузки по оси z определяются аналогично сжимающей, по значениям δ и β, используя необходимые кривые из графика рис.6.3, в.
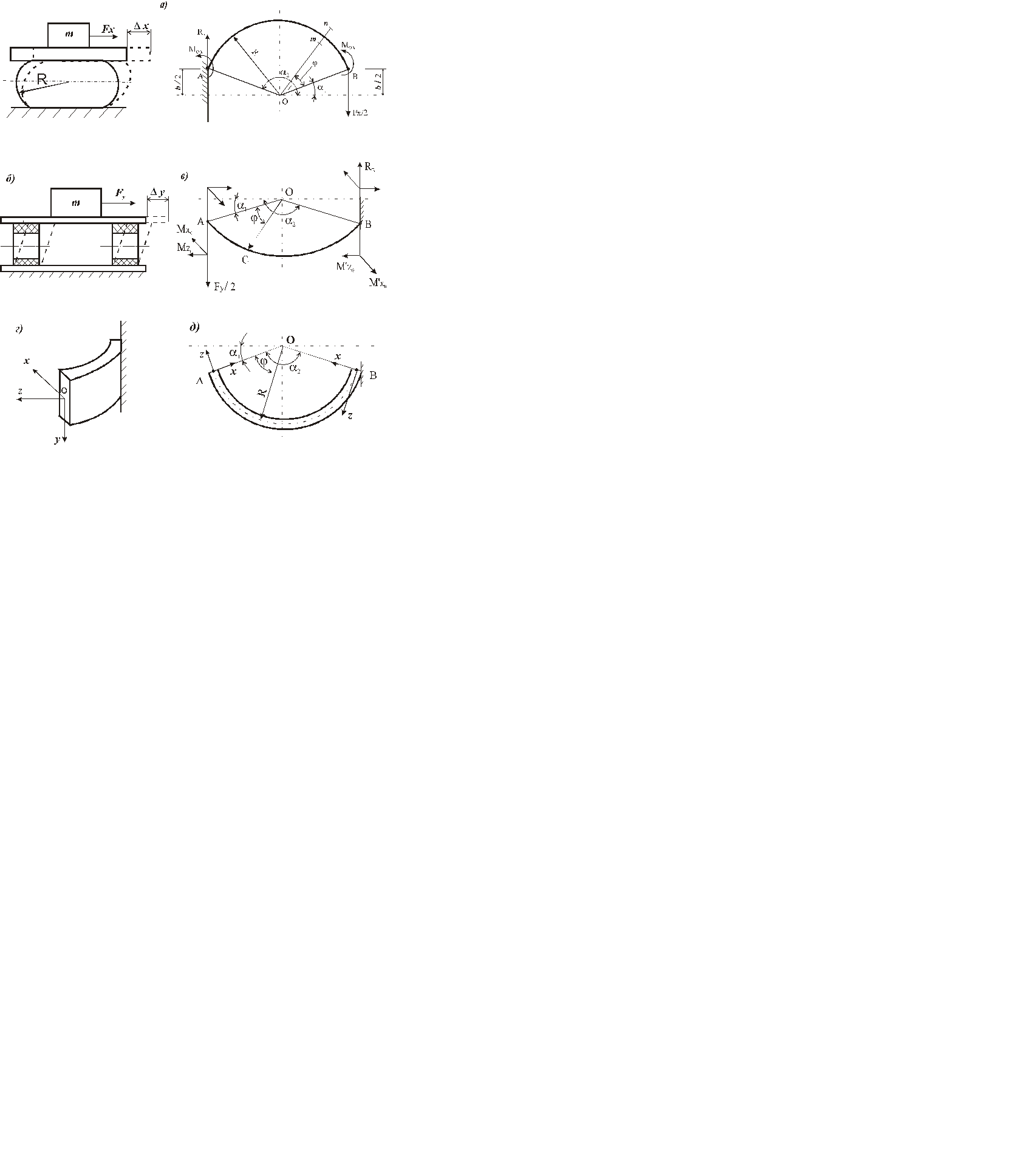
Рис. 6.5. К расчету жесткости КРКВ при деформациях «перекатывания» и поперечного сдвига кольца: а) нагрузки и деформации при «перекатывании» по оси х; б) нагрузки и деформации при поперечном сдвиге по оси у; в,г,д) схемы нагрузок и деформаций при поперечном сдвиге по оси у
9. Деформации “перекатывания” КРКВ в направлении оси x под действием сил Fx и Fy деформации виброизолятора малы, по сравнению с его размерами и осадкой от веса Fz объекта виброизоляции. И, кроме того, экспериментально установлено, что зависимости сила-деформация по осям x и y близки к линейным, даже при значительных нагрузках. Это позволяет воспользоваться методом Кастилиано [12] определения деформаций в кривых брусьях.
Вследствие симметрии кольца рассматриваем одну из его половин. При этом имеем в виду, что часть упругого элемента не участвует в деформациях, так как прижата крепежными планками 9 шириной b (рис.6.2,). Рабочая часть полукольца сосредоточена в интервале углов 
 (рис.6.5, а). Расчет ведем для случая, когда ширина крепежной планки b= 0,65 R, при величинах
(рис.6.5, а). Расчет ведем для случая, когда ширина крепежной планки b= 0,65 R, при величинах  . В точках А и В будут действовать силы Fx / 2 = RА и моменты Мi, которые препятствуют повороту сечения резинокордовой оболочки в этих точках.
. В точках А и В будут действовать силы Fx / 2 = RА и моменты Мi, которые препятствуют повороту сечения резинокордовой оболочки в этих точках.
Определим моменты, действующие в точках А и В. 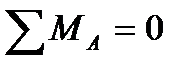 .
.
В развернутом виде 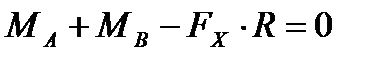 . Вследствие симметрии полукольца МА = МВ = Мпк . Тогда 2 Мпк = Fx. R. Откуда:
. Вследствие симметрии полукольца МА = МВ = Мпк . Тогда 2 Мпк = Fx. R. Откуда:
Мпк=Fx.R/2. (6.8)
Для поперечного сечения m1n1 (рис.6.5, а), наклоненного под углом 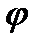 к линии радиуса ОВ, изгибающий момент равняется:
к линии радиуса ОВ, изгибающий момент равняется:
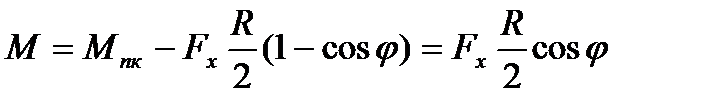 . (6.9)
. (6.9)
Полная энергия деформации, накопленная в кольце, определяется из выражения [12]:
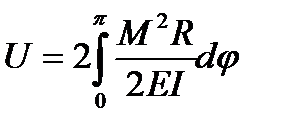 . (6.10)
. (6.10)
Следовательно, деформация с учетом пределов интегрирования от α 1 до α 2 равна:
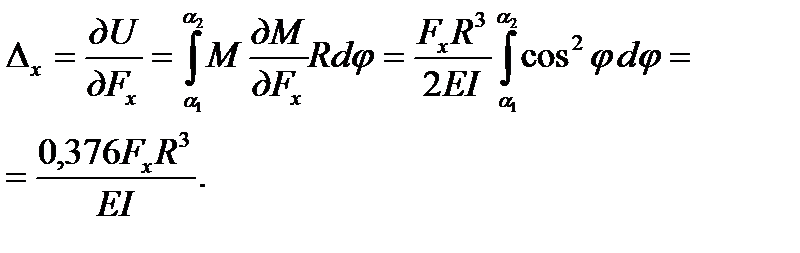 ( 6.11)
( 6.11)
Отсюда коэффициент статической жесткости при «перекатывании» в направлении оси x равен:
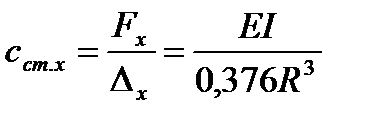 . (6.12 )
. (6.12 )
10. Деформация сдвига КРКВ при поперечном сдвиге в направлении оси y. Особенностью деформации амортизатора под действием силы Fy является то, что верхнее и нижнее его сечение в точках крепления к объекту виброзащиты и основанию перемещаются относительно друг друга параллельно без поворота (рис. 5, б).
В данном случае учитываем изгиб оболочки и её кручение. Закрепим амортизатор на вертикальной стенке таким образом, чтобы ось y заняла вертикальное положение (рис.6.5, г).Вследствие симметрии рассматриваем половину кольца (рис.6.5, в,д). Рассматриваем только малые вертикальные перемещения КРКВ вдоль оси у, пренебрегая перемещениями в горизонтальной плоскости xoz, как малыми величинами высшего порядка.
Анализируя действующие нагрузки в точке А, приходим к выводу, что к ней приложены вертикальная сила Fy /2, а также моменты Мхо и Мzо, препятствующие повороту сечения виброизолятора в точке А. При этом в точке В будет действовать реакция RB = Fy /2 и моменты М 1 хо и М 1 zо, поскольку сечение в точке В также не поворачивается и остается параллельным относительно сечения в точке А.
Находим момент Mzo. Σ М в= 0. По аналогии с п.9 - Мzо= М 1 zо, тогда в развернутом виде 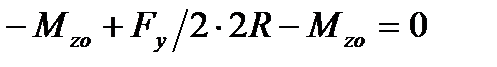 .
.
Откуда
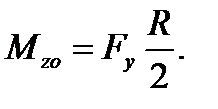 ( 6.13)
( 6.13)
Величина момента Мхо может быть определенаиз уравнения статики. Находим её согласно известной из сопромата теореме о наименьшей работе:
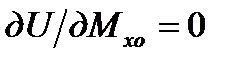 (6.14)
(6.14)
Моменты Мх и Мz в каком-либо поперечном сечении, проходящем через точку “ С “ (рис.6.5, в), будут равны:
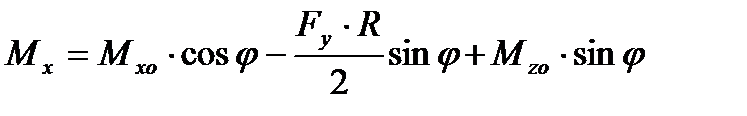 ; (6.15 )
; (6.15 )
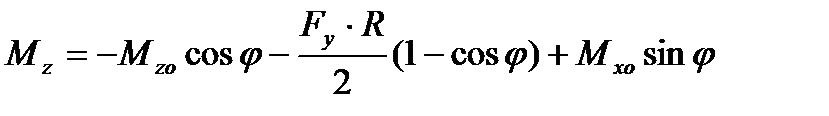 . (6.16)
. (6.16)
Из сопромата известно, что выражение для потенциальной энергии деформации представляется в таком виде: 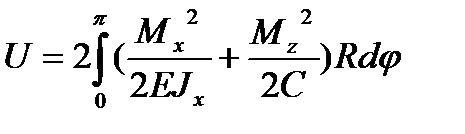 (6.17)
(6.17)
Подставляя его в уравнение ( 6. 14), с учетом новых пределов интегрирования и того, что
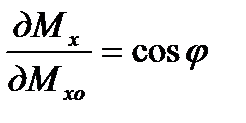 ,
, 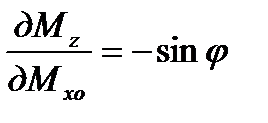 ,
,
получаем
| (6.18) |
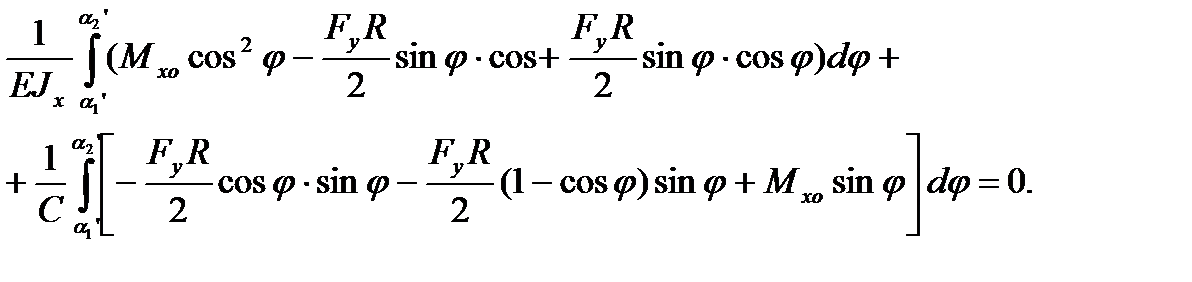 Откуда
Откуда 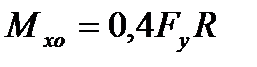 .
.
Перемещение точки А определим при помощи теоремы известной из классического курса сопромата [12]: 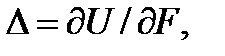
где значение U подставляем из уравнения ( 6.17 ). Учитывая, что
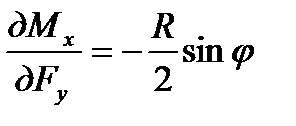 ;
; 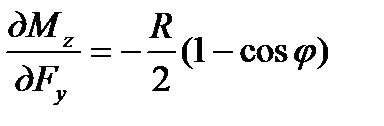 , (6.19 )
, (6.19 )
получаем
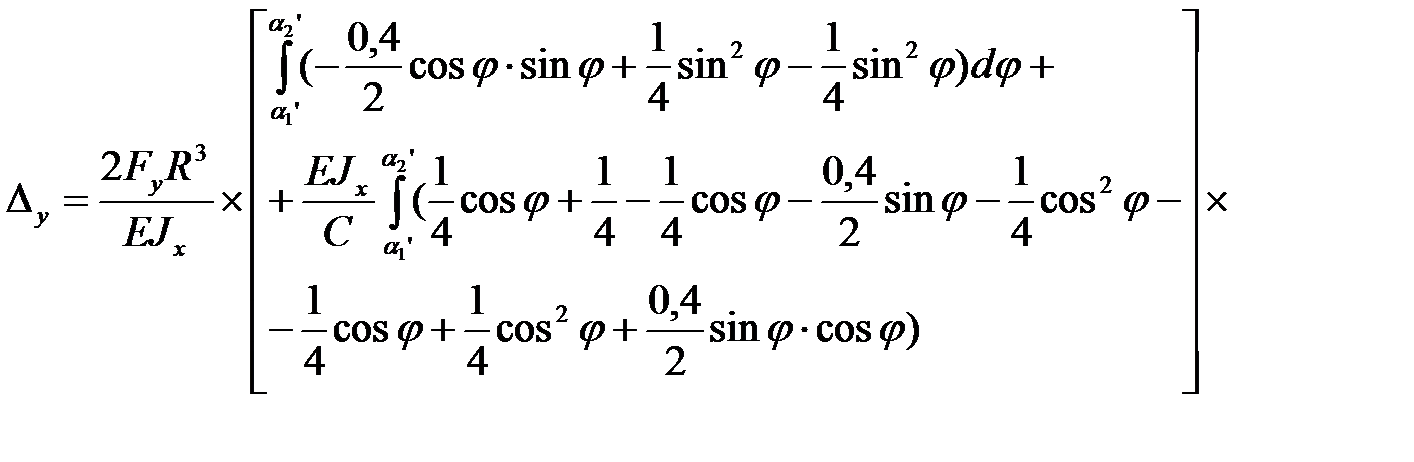
| (6.20) |
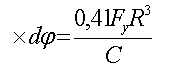
где С - постоянная, называемая жесткостью при кручении.
Для прямоугольного поперечного сечения бруса [12]:
 (6.21)
(6.21)
где G = 1/3 E – модуль сдвига материала виброизолятора.
Коэффициент 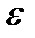 зависит от отношения l / h (рис.6.4, в), значения которого приведены в табл.6.1 [12]:
зависит от отношения l / h (рис.6.4, в), значения которого приведены в табл.6.1 [12]:
Из выражения ( 6.20) определяем коэффициент статической жесткости КРКВ при поперечном сдвиге в направлении оси у:
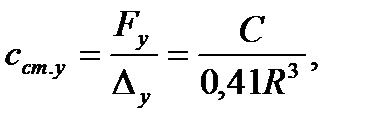 (6.22)
(6.22)
Таблица 6.1
Date: 2015-10-21; view: 611; Нарушение авторских прав