Оборудования горной машины на кольцевых

резинокордовых амортизаторах

Чаще всего при описании динамической модели и расчетах пассивных систем снижения динамических нагрузок пользуются линейными динамическими моделями.

Как показали исследования КРКВ, что наряду с повышенным коэффициентом потерь ν = 0,26-0,45, они имеют нелинейную характеристику динамической жесткости [1]:

; (23)

, (24)

где c_cm.x,y,z – статические жесткости, рассчитанные по формулам

(6.7), (6.12) и (6.22);

k_x, ≈ k_y =5,0; k_z =2,85 – эмпирические коэффициенты [1];

u – амплитуда колебаний объекта на амортизаторе отно-cительно основания (источника вибрации) u = z - z’ (рис.6.6);

δ – относительная деформация кольца (рис.6.3 ,в).

В известных системах виброизоляции (сокращенно СВ) с применением сетчатых амортизаторов, у которых очень близкая с КРКВ нелинейность коэффициента жесткости , при математическом описании динамической модели В.С. Ильинским [13] было принято допущение, что до резонанса колебания основания СВ и объекта снижения динамических нагрузок происходят в «фазе», а после резонанса – в «противофазе». С целью определения возможности применения данного допущения в нашем случае построим фазочастотные характеристики для величин параметров диссипации близких к КРКВ. Первоначально принимаем допущение о линейности коэффициента жесткости. Тогда динамическая модель такой СВ (рис.6.6) при кинематическом возбуждении, например, по оси z описывается уравнением:

_, (6.25)

где m –масса виброизолируемого объекта;

z – координата перемещения массы;

z’ – координата перемещения основания.

Для отыскания частного решения уравнения ( 6.25 ) используем метод комплексных амплитуд [2]. Введем понятие комплексной величины действительная часть которой, совпадает с выражением для смещения:

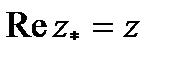. (6.26)

Пусть основание возбуждается гармоническими колебаниями вида

, или

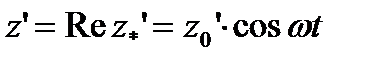. (6.27)

Рис. 6.6. Динамическая модель системы виброизоляции

Date: 2015-10-21; view: 334; Нарушение авторских прав