
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема: Перевірка гетероскедастичності. Побудова моделі з наявністю гетероскедастичності
|
|
Мета заняття: При дослідженні залежності витрат на харчування від доходу істотно припустити, що дисперcія залишків може змінюватись для різних груп населення за розміром доходів.
На основі статистичних даних:
ü перевірити гіпотезу про наявність гетероскедастичності;
ü користуючись  - критерієм та параметричним тестом Гольдфельда—Квандта, побудувати математичну модель залежності витрат на харчування від доходу.
- критерієм та параметричним тестом Гольдфельда—Квандта, побудувати математичну модель залежності витрат на харчування від доходу.
Хід роботи
Ідентифікуємо змінні моделі:
 — витрати на харчування, залежна змінна;
— витрати на харчування, залежна змінна;
 — загальні затрати, незалежна змінна;
— загальні затрати, незалежна змінна;
 .
.
 Виходячи з особливостей вихідної інформації, можна припустити, що порушується гіпотеза про незмінність дисперсії.
Виходячи з особливостей вихідної інформації, можна припустити, що порушується гіпотеза про незмінність дисперсії.
1. Завантажити програму EXCEL.
2. Сформувати таблицю вихідних даних, заповнивши діапазон комірок A2:B19 (мал. 1).
Для визначення гетерескедастичності моделі використовуємо алгоритм Гольдфельда - Квандта.
3. Для впорядкування даної сукупності спостережень по змінній  від меншого до більшого, використовуємо функцію Сортировка із меню Данные. У вікні, яке відкривається після виклику цієї команди вказуємо змінну, по якій необхідно відсортувати масив даних.
від меншого до більшого, використовуємо функцію Сортировка із меню Данные. У вікні, яке відкривається після виклику цієї команди вказуємо змінну, по якій необхідно відсортувати масив даних.
4. Для кожної групи знайдемо середнє значень залежної змінної  . Для цього використовуємо функцію СРЗНАЧ, параметрами якої вкажемо відповідні масиви. Та суму квадратів відхилень значень залежної змінної від середнього по цій групі
. Для цього використовуємо функцію СРЗНАЧ, параметрами якої вкажемо відповідні масиви. Та суму квадратів відхилень значень залежної змінної від середнього по цій групі  . Для обчислення сум використаємо функцію å, що знаходиться на стандартній панелі інструментів EXEL.
. Для обчислення сум використаємо функцію å, що знаходиться на стандартній панелі інструментів EXEL.
5. Для визначення кількості спостережень в кожній групі, а також усього, використовуємо функцію ЧСТРОК.
6. Необхідні для подальших обчислень частки  та
та  по кожній групі знайдемо у відповідних комірках.
по кожній групі знайдемо у відповідних комірках.
7. Обчислюємо значення 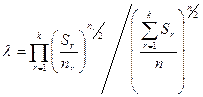 , де n - загальна сукупність спостережень;
, де n - загальна сукупність спостережень;
nr - кількість спостережень r -ї групи. Для цього:
- для знаходження добутку  використовуємо функцію ПРОИЗВЕД, тобто, у комірку I21 вписуємо формулу I21:=ПРОИЗВЕД(I5;I12;I18);
використовуємо функцію ПРОИЗВЕД, тобто, у комірку I21 вписуємо формулу I21:=ПРОИЗВЕД(I5;I12;I18);
- у комірці I22 знайдемо суму  (k=1,2,3);
(k=1,2,3);
- у комірці I23 знайдемо 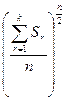 , для цього у комірку занесемо формулу I23:=(I22/D21)^(D21/2);
, для цього у комірку занесемо формулу I23:=(I22/D21)^(D21/2);
- у комірці I24 знайдемо  (I24:=I21/I23).
(I24:=I21/I23).
8. Розрахуємо критерій  за формулою:
за формулою:  у комірці I25, використовуючи вбудовану функцію LN.
у комірці I25, використовуючи вбудовану функцію LN.
9. Обчислюємо табличне значення критерію, використовуючи вбудовану функцію ХИ2ОБР, параметрами якої є рівень значущості та ступінь свободи, які вказані у відповідних комірках. Тобто у комірку D24 вносимо формулу D24: =ХИ2ОБР(E22;D23).
10. Порівняємо  з критерієм
з критерієм  , робимо висновок.
, робимо висновок.
11.
 |
Після проведених обчислень робочий лист EXEL приблизно може виглядати так, як на рис. 2.
12. Перевіримо наявність гетероскедастичності для наведених вихідних даних на основі параметричного тесту Гольдфельда—Квандта.
13. Запишемо впорядкований за  масив даних у блок A28:B46. Кількість спостережень обчислимо за допомогою функції ЧСТРОК у комірці E27.
масив даних у блок A28:B46. Кількість спостережень обчислимо за допомогою функції ЧСТРОК у комірці E27.
14. Обчислюємо кількість відкинутих елементів за формулою:  у комірці G27. Для того, щоб мати найближче ціле до отриманого числа, використовуємо функцію ОКРУГЛВНИЗ. Тобто у комірку G27 запишемо формулу G27:=ОКРУГЛВНИЗ((E27*4)/15;0).
у комірці G27. Для того, щоб мати найближче ціле до отриманого числа, використовуємо функцію ОКРУГЛВНИЗ. Тобто у комірку G27 запишемо формулу G27:=ОКРУГЛВНИЗ((E27*4)/15;0).
15. Розрахуємо параметри лінійної регресії для першої та другої отриманих сукупностей даних. В пакеті EXEL є декілька можливостей для цього. Скористаємося функціями НАКЛОН та ОТРЕЗОК які повертають значення кутового коефіцієнта та вільного доданка рівняння лінійної регресії відповідно. Аргументами цих функцій є масиви даних  та
та  , для яких будується регресія. Тому, наприклад, у комірку D30 занесемо формулу D30:=НАКЛОН(A29:A35;B29:B35), а у комірку D33 – формулу D33:=ОТРЕЗОК(A29:A35;B29:B35).
, для яких будується регресія. Тому, наприклад, у комірку D30 занесемо формулу D30:=НАКЛОН(A29:A35;B29:B35), а у комірку D33 – формулу D33:=ОТРЕЗОК(A29:A35;B29:B35).
16. У блоках E29:E35 та E40:E46 обчислюємо розрахункові значення показника 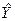 . Запишемо у комірку E29 формулу Е29:=$D$30*B29+$D$33 та зкопіюємо її на весь діапазон. Нагадаємо, що знак “$” вказує на абсолютну адресацію до відповідної комірки.
. Запишемо у комірку E29 формулу Е29:=$D$30*B29+$D$33 та зкопіюємо її на весь діапазон. Нагадаємо, що знак “$” вказує на абсолютну адресацію до відповідної комірки.
17. У блоках F29:G35 F40:G46 обчислюємо залишки моделі та квадрати залишків. У комірках G36 та G47 обчислюються суми квадратів залишків моделі: G36:=СУММ(G29:G35).
18. Знайдемо критерій  за формулою:
за формулою:  . Для цього у комірку B49 внесемо формулу В49:=(G47/D47)/(G36/D36), де у комірках D36 та D47 знайдено кількість спостережень першої та другої сукупності відповідно.
. Для цього у комірку B49 внесемо формулу В49:=(G47/D47)/(G36/D36), де у комірках D36 та D47 знайдено кількість спостережень першої та другої сукупності відповідно.
19. Знайдемо критичне значення F-критерію. Визначаємо спочатку ступені свободи  та
та  . Тобто, у комірки E49 та G49 запишемо формули: E49:=D36-2 та G49=D47-2 відповідно. Задамо рівень значущості
. Тобто, у комірки E49 та G49 запишемо формули: E49:=D36-2 та G49=D47-2 відповідно. Задамо рівень значущості  , обчислимо Fтабл, скориставшись функцією FРАСПОБР, параметрами якої є рівень значущості і ступені свободи. Тобто, у комірку D50 запишемо формулу D50:=FРАСПОБР(B50;E49;G49).
, обчислимо Fтабл, скориставшись функцією FРАСПОБР, параметрами якої є рівень значущості і ступені свободи. Тобто, у комірку D50 запишемо формулу D50:=FРАСПОБР(B50;E49;G49).
20.
 |
Оскільки в нашому випадку
 , робимо висновок про наявність гетероскедастичності.
, робимо висновок про наявність гетероскедастичності.
21. Приблизний вигляд робочого вікна EXEL після проведених розрахунків приведено на рис. 3.
22. Оскільки два тести показами наявність гетегоскедактичності, Побудуємо оператор оцінювання за методом Ейткена. Приблизний вигляд робочого вікна EXEL після виконаної роботи може бути як на рис. 4.
23. У комірках C53:C70 обчислюємо значення  за формулою:
за формулою:  , тому, запишемо у комірку C53 формулу C53:=1/B53 і протягнемо її на весь діапазон C53:C70.
, тому, запишемо у комірку C53 формулу C53:=1/B53 і протягнемо її на весь діапазон C53:C70.
24. Поруч, у стовбчику D53:D70 знайдемо добутки 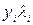 . У рядку A71:D71 обчислюємо суми.
. У рядку A71:D71 обчислюємо суми.
25. 
Будуємо матрицю  Оскільки самі матриці є дуже громіздкими, можна обійтися без їх явної побудови, а скориставшись знаннями з лінійної алгебри, побудувати її зразу у комірках B74:C75, де: B73=C71=
Оскільки самі матриці є дуже громіздкими, можна обійтися без їх явної побудови, а скориставшись знаннями з лінійної алгебри, побудувати її зразу у комірках B74:C75, де: B73=C71= 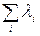 , C73=C72=n- кількості спостережень, аналогічно, B74=n; C74=B71=
, C73=C72=n- кількості спостережень, аналогічно, B74=n; C74=B71=  .
.
26. Для знаходження оберненої матриці  скористаємося вбудованою функцією МОБР, яка повертає обернену матрицю. Порядок дій наступний: записуємо у комірку E74 формулу E74:=МОБР(B73:C74), потім при натиснутій лівій кнопці миші помічаємо діапазон E74:F75, де буде знаходитись обернена матриця, натискаємо клавішу F2 і потім комбінацію клавіш Ctrl+Shift+Enter.
скористаємося вбудованою функцією МОБР, яка повертає обернену матрицю. Порядок дій наступний: записуємо у комірку E74 формулу E74:=МОБР(B73:C74), потім при натиснутій лівій кнопці миші помічаємо діапазон E74:F75, де буде знаходитись обернена матриця, натискаємо клавішу F2 і потім комбінацію клавіш Ctrl+Shift+Enter.
27. У діапазоні B76:B77 будуємо добуток матриць  : в клітинку B76 копіюємо суму добутків
: в клітинку B76 копіюємо суму добутків 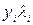 , а в клітинку B77 суму значень показника..
, а в клітинку B77 суму значень показника..
28. У діапазоні D76:D77 знайдемо матрицю оцінок параметрів моделі, як добуток матриць  , для цього скористаємося вбудованою матричною функцією МУМНОЖ поставивши курсор миші в клітинку D76, викликаємо функцію МУМНОЖ, у вікні, що з’явиться, вказуємо блоки, де знаходяться вихідні матриці
, для цього скористаємося вбудованою матричною функцією МУМНОЖ поставивши курсор миші в клітинку D76, викликаємо функцію МУМНОЖ, у вікні, що з’явиться, вказуємо блоки, де знаходяться вихідні матриці  та
та  (див. мал. 4) і далі діємо, як в п. 26.
(див. мал. 4) і далі діємо, як в п. 26.
29. Тепер відома модель, яка побудована у відповідності до прийнятої гіпотези щодо наявності гетероскедастичності, вона має вигляд: 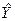 =2,0223+0,0138
=2,0223+0,0138  .
.
30. Згідно з моделлю обчислимо розрахункові значення показника в діапазоні E53:E70. Для цього у комірку E53 записуємо формулу E53:=$F$76+$F$77*B53 і копіюємо її на весь діапазон. Зауважимо, що знак “$” означає абсолютну адресацію до комірки.
31. У наступних чотирьох рядках розраховуємо похибки моделі  , квадрати похибок
, квадрати похибок  , відхилення значень показника від середнього
, відхилення значень показника від середнього  та квадрати відхилень показника від середнього.
та квадрати відхилень показника від середнього.
32. У комірках H72:H76 розраховуємо 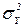 ,
,  ,
,  та
та  відповідно, за формулами:
відповідно, за формулами:
 ,
, 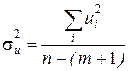 ,
,  ,
, 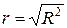 ,
,
де  об’єм спостережень,
об’єм спостережень, 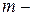 кількість факторів моделі. Зробимо відповідні висновки.
кількість факторів моделі. Зробимо відповідні висновки.
33. У комірках B78:C79 розрахуємо коваріаційну матрицю моделі. Для реалізації формули:
 ,
,
запишемо у комірку B78 формулу B78:=H74*E74:F75 і повторимо порядок установки формули масива, як в у п 26.
При правильному виконанні в діапазоні В78:С79 буде знайдена коваріаційна матриця.
34. На головній діагоналі цієї матриці знаходяться квадрати стандартних похибок моделі. Тому в клітинках B80, B81 і знаходимо стандартні похибки: B80=:КОРЕНЬ(B78), B81:=КОРЕНЬ(B79) за допомогою вбудованої функції КОРЕНЬ.
35. Для знаходження критичного значення параметру Стьюдента скористаємося вбудованою функцією СТЬЮДРАСПОБР(0,05;12),параметрами якої вкажемо рівень значущості 0,05 та кількість ступенів свободи (див. ком. D79:E79 рис.4).
36. У блоках D80:F81 та D81:F81 знайдемо довірчі інтервали для оцінок параметрів моделі. Зробимо відповідні висновки.
37. Таким чином, два тести вказують на наявність гетероскедастичності. Це означає, що модель треба будувати з урахуванням цьго факту, тобто, за допомогою узагальненого методу найменших квадратів, або методу Ейткена.
Date: 2015-10-19; view: 681; Нарушение авторских прав