Тема: Побудова моделі при наявності автокореляції залишків

Мета заняття:

ü На основі вихідних даних побудувати модель даної залежності у вигляді лінійного рівняння.

ü Знайти оцінки параметрів лінії регресії по даній стохастичній залежності.

ü Оцінити адекватність моделі статистичним даним з ймовірністю Р=0,95.

ü З ймовірністю Р=0,95 визначити наявність автокореляції в залишках.

ü У випадку наявності автокореляції в залишках, побудувати модель даної залежності за допомогою методу Ейткена.

ü Визначити наявність автокореляції у залишках для отриманої моделі. Зробити висновки.

ü З ймовірністю Р=0,95 визначити адекватність отриманої моделі експериментальним даним.

Хід роботи

1. Завантажити програму EXCEL.

2. Сформувати таблицю вихідних даних, заповнивши діапазон комірок А3:С12 (рис.1).

3. У комірці L2 за допомогою вбудованої функції ЧСТРОК знайдемо об’єм вибірки n: L2:=ЧСТРОК(A3:B12).

4. Для того, щоб не витрачати час на побудову рівняння лінійної регресії для вихідних даних, скористаємося тими можливостями, які є в EXCEL. А саме, функціями НАКЛОН – яка повертає значення кутового коефіцієнта рівняння лінійної регресії, і ОТРЕЗОК, яка повертає ординату точки перетину лінії регресії з віссю OY. Аргументами цієї функції треба вказати діапазони знаходження значень змінної Y та змінної X. Тобто, у комірки K3 і K4 внесемо відповідно формули: K3:=ОКРУГЛ(ОТРЕЗОК(B3:B12;C3:C12);3) та K4:=ОКРУГЛ(НАКЛОН(B3:B12;C3:C12);3) (рис.2).

5. Для подальшого використання нам необхідні значення 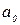та що знаходяться у комірках K3 і K4. Щоб уникнути абсолютних посилань на ці комірки, скористаємося ще однією можливістю EXCEL – створення імен. На такі імена можна в подальшому посилатися, як на вбудовані константи або змінні. Для цього:

- ставимо курсор у комірку K3 де знаходиться значення ;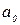

- в підрозділі ВСТАВКА головного меню обираємо пункт Имя і далі підпункт Присвоить;

- у відкритому вікні цієї команди у полі Формула вказуємо адресу комірки, в якій знаходиться дана величина, а у полі Им я задаємо її ім’я (рис.3).

Так можна створити імена: n- кількість спостережень; Ra0-константа a0; Ra1- константа a1.

6. У діапазоні D3:D12 знаходимо розрахункові значення показника. Для цього:

- у комірку D3 заносимо формулу: D3:=Ra0+Ra1*C3 (як бачимо, тут замість абсолютних посилань вказано відповідні імена);

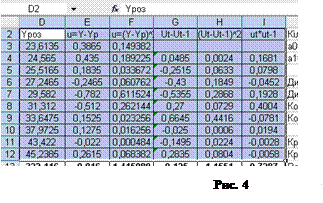- залишивши цю комірку активною, наводимо курсор миші при натиснутій лівій кнопці в правий нижній кут і протягуємо цю формулу на весь діапазон D3:D12;

- після того, як курсор миші відпустити, у комірках діапазона залишаються потрібні формули.

Зауважимо при цьому, що посилання на імена констант Ra0 та Ra1- не змінюються.

7. У блоці E3:E12 знайдемо залишки моделі. Для цього запишемо у комірку E3 формулу: E3:=B3-D3 і скопіюємо її на весь блок Е3:Е12.

8. Для знаходження u² у комірку F3 запишемо формулу: F3:=E3^2 і скопіюємо її на блок F3:F12.

9. У блоці G4:G12 знайдемо різниці відповідного і попереднього залишку моделі, а у діапазоні H4:H12 квадрати отриманих різниць (знайти самостійно).

10. У блоці I4:I12 знайдемо добутки відповідного і попереднього залишків моделі (рис.4).

11. У діапазоні В13:I13 знайдено суми по відповідним стовпчикам.

Це можна зробити за допомогою кнопки “Автосумма”, яка знаходиться на стандартній панелі робочого вікна EXEL.

Для цього ставимо курсор у комірку В13 і швидко натискаємо курсором миші на значок. При цьому EXEL покаже, який діапазон буде сумуватися. Якщо ви згодні, відпустіть кнопку миші, якщо ні, самостійно обведіть, при натиснутій лівій кнопці миші, потрібний діапазон.Скопіюйте отриману у комірці В13 формулу на весь діапазон В13:I13 (рис.5).

12. У діапазоні K6:K9 знаходимо необхідні статистики: дисперсію показника, дисперсию залишків, коефіцієнт детермінації, коєфіцієнт кореляції. Зауважимо, що для їх знаходження можна використати як відомі методи (див. лаб.1-2), так і вбудовані функції EXEL. Так, у комірках знаходяться формули: K6:=F13/(n-2); К7:=ДИСП(B3:B12); К8: =(K7-K6)/K7; К9:=КОРЕНЬ(K8).

13. Знайдемо критерій Дарбіна-Уотсона за формулою: . Для цього у комірку K11 занесемо формулу: K11:=H13/F13.

14. Порівняємо значення критерію DW з табличним при a=0,05 і n=10. Критичні значення критерію DW у цьому випадку: DW ₁=0,879 - нижня межа; DW₂ =1,320 - верхня межа.

Оскільки DWфакт < DW ₁ , то при можна стверджувати, що залишки u_t мають додатню автокореляцію.

Наявність чи відсутність автокореляції залишків можна також визначити на основі критерію фон Неймана.

15. Для знаходження критерію фон Неймана за формулою: занесемо у комірку K12 формулу: K12:=(n/(n-1))*K11.

16. Це значення порівнюється з табличним _табл = 1,18 при n=10 і a=0,05. Оскільки _факт < _табл, то існує додатня автокореляція залишків.

Отримані значення критеріїв дають підставу до прийняття гіпотези про наявність автокореляції (рис.6).

17. Для побудови нової моделі за методом Ейткена, необхідно обчислити параметр . Для цього у комірку K13 занесемо формулу: K13:=(n/(n-1))*(I13/F13)+(2/n).

18. У діапазоні B15:K24 будуємо матрицю . На рис.7 представлено цей діапазон у режимі відображення формул.

19. Побудуємо обернену до матрицю. Хоча в EXEL є функція для знаходження оберненої матриці, але вона дає наближений результат, тому в даному випадку побудуємо обернену матрицю самостійно, скориставшись формулою. Відповідний діапазон в режимі відображення формул показано на рис.8.

20. У діапазоні M15:N24 представимо матрицю , а у діапазоні B37:K38 – транспоновану до матриці .

21. Для цього скористаємося функцією ТРАНСП, яка повертає транспоновану матрицю:

- ставимо робочий курсор в ячейку B37 заносимо формулу B37:=ТРАНСП(M15:N24);

- при натиснутій лівій кнопці миші помічаємо блок B37:K38 і натискаємо кнопку F2 а потім комбінацію Ctrl+Shift+Enter.

Таким чином ми внесемо в цей діапазон матричну формулу (рис.9,10).

22. Знайдемо матрицю у діапазоні B40:C41:

- ставимо курсор миші в клітинку B40 і вносимо формулу

40:=МУМНОЖ(МУМНОЖ(B37:K38;B26:K35);M15:N24) для подвійного добутку матриць;

- при натиснутій лівій кнопці миші помічаємо діапазон B40:C41;

- аналогічно попередніх пунктів натискаємо комбінацію клавіш: F2 а потім Ctrl+Shift+Enter.

23. Аналогічно отримуємо матриці (діапазон Н40:I41) та (діапазон Е40:Е41).

Для того, щоб отримати обернену матрицю, використовуємо вбудовану функцію МОБР.

Порядок використання цієї функції аналогічний п.17 (рис.11).

24. Аналогічно отримуємо у діапазоні K40:K41 матрицю (рис.12).

25. Аналогічно п.6-п.11 отримаємо у блоці A43:H53 усі необхідні для подальшого дані, а саме:

- нові розрахункові значення показника (діапазон D44:D53) (рис.13) з оцінками параметрів та 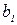(рис.12);

- залишки моделі (діапазон Е44:Е53);

- квадрати залишків моделі (діапазон F44:F53);

- різниці відповідного і попереднього залишків моделі (діапазон G45:G53);

- квадрати різниці відповідного і попереднього залишків моделі (діапазон Н45:Н53);

- у рядку B54:H54 утворюємо суми по відповідним рядкам.

26. У комірці K45 розрахувати значення критерію Дарбіна-Уотсона K45:=H54/F54 (рис.14).

27. Порівнявши його з критичним значенням при n=10 і a=0,05, коли DW факт < DW ₁, приходимо до висновку, що ми не звільнились від автокореляції залишків. Це означає, що вихідна гіпотеза, коли залишки описуються авторегресійною схемою першого порядку, не дотримується. Якщо залишки описуються авторегресійною схемою більш високого порядку, то доцільно виконати оцінку параметрів моделі методом Кочрена-Оркатта або Дарбіна.

28. Підвести підсумки лабораторної роботи і зробити висновки.

29. Зберегти книгу у своїй робочій папці під ім'ям Лаб.10.

ЛАБОРАТОРНА РОБОТА № 10

Date: 2015-10-19; view: 434; Нарушение авторских прав