При подсчете вероятностей случайных событий по классической формуле применяется теория соединений и правило произведения

Группы элементов, отличающиеся порядком или составом элементов, называются соединениями. Соединения бывают трех видов: размещения, перестановки и сочетания.

Размещениями из S элементов по К называются соединения, отличающиеся или порядком элементов, или хотя бы одним элементом. Размещения обозначаются (от французского “ arrangement ” - размещения) и вычисляются по формуле:

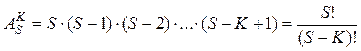
Пример:

Задача 1.1. Сколькими способами можно набрать шестизначный номер телефона, если помнить, то все цифры различны?

.

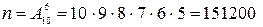Перестановками из К элементов называются соединения, каждое из которых содержит К элементов и которые отличаются одно от другого только порядком расположения элементов (это ). Обозначаются перестановки Р_К (от французского слова “ permutation ” - перестановка) и вычисляется по формуле:

Задача 1.2. Сколькими способами можно разместить 3-х студентов за одной партой?

.

Сочетаниями из S элементов по К называются такие соединения, которые отличаются между собой хотя бы одним элементом. Обозначаются сочетания (от французского слова “ combination ”- комбинация) и вычисляются по формуле:

.

Задача 1.3. Сколькими способами можно выбрать трех делегатов на конференцию из группы, в которой 25 студентов?

.

Легко показать, что , т.е. .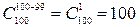

Правило произведения заключается в следующем:

если элемент a₁ можно выбрать n₁ способами, после каждого выбора этого элемента следующий за ним элемент а₂ можно выбрать n₂ способами, …, после выбора элементов а₁ …, а_к-1 элемент а_к выбирается n_к способами, то последовательность k элементов (а₁, а₂, …, а_к) можно выбрать:

способами.

Задача 1.4. Сколькими способами можно составить команду игроков, состоящую из 1 вратаря, 2 защитников и 3 нападающих, если имеются 2 вратаря, 7 защитников и 9 нападающих?

.

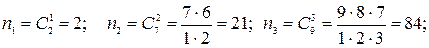
При решении многих задач применяется также непосредственный подсчет способов отбора.

Задача 1.5. Сколькими способами можно составить набор из 2-х игральных костей, чтобы сумма очков на верхних гранях была равна 7?

І-я: 1 2 3 4 5 6

ІІ-я: 6 5 4 3 2 1

Задача 1.6. Имеется 7 слитков: 4 слитка изготовленны в 1-м цехе и 3 изготовлены во 2-м. Наугад берут 3 слитка. Какова вероятность того, что среди отобраных есть 2 слитка, изготовленные в 1-м цехе?

Ε – выбор 3-х слитков из 7,

А – появление двух слитков из 1-го цеха и 1 слитка из 2-го цеха.

Число исходов конечно. Они несовместимы, равновозможны и образуют полную группу. Применяем классическое определениие:

.

Задача 1.7. Заявка предприятия на оборудование может поступить в любое время суток. Найти вероятность того, что заявка поступит в первой половине дня (от 6 часов до 1 часов).

Ε – поступление заявки в любое время суток

А - поступление заявки от 6 до 12 часов.

Всех равновозможных исходов опыта (моментов поступления заявки) бесчисленное множество, поэтому применяем геометрическое определение вероятности:

.

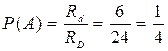Задача 1.8. Система состоит из 7 элементов. При проверке вышли из строя 2. Найти вероятность отказа элемента.

Ε – проверка элементов

А – выход элементов из строя.

Так как опыты были проведены (исходы неравновозможны), то применяем статистическое определение вероятности события А:

.

Date: 2015-10-18; view: 448; Нарушение авторских прав