Системы случайных величин

Основные понятия. Числовые характеристики системы случайных величин

Совокупность нескольких случайных величин, совместно характеризующих рассматриваемое случайное явление, называется системой случайных величин или векторной случайной величиной.

Систему n случайных величин 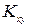обычно обозначат ().

Свойства системы случайных величин не исчерпываются свойствами отдельных величин, ее составляющих. Они включают также взаимные связи (зависимости) между случайными величинами.

Для геометрической интерпретации системы случайных величин пользуются образом случайной точки или случайного вектора в n -мерном пространстве (для системы n случайных величин).

При n =2 система интерпретируется точкой на плоскости с координатами () и т.д.

Числовые характеристики системы случайных величин, как и числовые характеристики обыкновенных случайных величин, представляются их соответствующими моментами.

Начальным моментом (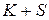)-го порядка системы двух случайных величин () называется математическое ожидание произведения К -й степени случайной величины Х на S -ю степень У:

Центральным моментом (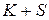)-го порядка системы двух случайных величин () называется математическое ожидание произведения К -й и S -й степеней соответствующих центрированных случайных величин

.

Особую роль характеристики системы случайных величин играет второй смешанный центральный момент

,

т.е. математическое ожидание произведения центрированных случайных величин. Введем для него обозначение К_ху. Для дискретных случайных величин К_ху выражается формулой:

а для непрерывных случайных величин – формулой:

.

Корреляционный момент, как и другие моменты второго порядка, характеризует рассеивание случайных величин. Но помимо этого данный момент описывает еще и связь между случайными величинами, входящими в систему.

Равенство нулю корелляционного момента есть необходимое условие независимости случайных величин.

Заметим сразу, что это условие не является достаточным, т.е. из равенства нулю корреляционного момента в общем случае не следует независимость случайных величин.

Из приведенных формул видно, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если хотя бы одна из величин мало отклоняется от своего математического ожидания (т.е. почти случайна), то корреляционный момент будет мал, как бы тесно не были связаны случайные величины Х и У.

Поэтому для характеристики связи между Х и У в чистом виде переходит от корреляционного момента 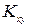к безразмерной характеристике:

,

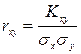где σ_х и σ_у – средние квадратические отклонения соответственно Х и У. Если , а значит и 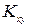, отличен от нуля, то случайные величины Х и У называются корреляционными. Случайные величины могут быть связаны вероятностной связью, при которой каждому значению одной случайной величины соответствует некоторое распределение другой. Например, вес и рост человека – две случайные величины, между которыми существует вероятностная связь (зависимость). Мы не можем сказать, что для каждого значения роста человека существует строго определенный вес. Вес может колебаться в довольно широких пределах. Однако здесь может быть указана тенденция увеличения веса при увеличении роста.

Если при изменении значений одной случайной величины другая испытывает изменение своего математического ожидания (т.е. тем самым проявляя тенденцию к изменению своих значений), то такой вид вероятностной зависимости между случайными величинами называется корреляционной связью или зависимостью.

Таким образом, корреляционная зависимость – это разновидность вероятной зависимости. Например, на изменение значений одной величины, другая величина может реагировать изменением своей дисперсии или других характеристик.

Корреляционная зависимость это наиболее важная, с точки зрения практики, зависимость между случайными величинами. Она выражается в виде функциональных зависимостей математического ожидания одной случайной величины от значений другой, т.е. в виде функций и , представляющих собой условные математические ожидания одних случайных величин при рассмотрении других в качестве независимых переменных (аргументов).

Функциональные зависимости и называются соответственно регрессией Х на У и регрессией У на Х. Графическое из изображение носит название линий или кривых регрессии. В зависимости от вида функций и различают линейную корреляционную зависимость, квадратичную, показательную, гиперболическую и т.д.

Наиболее часто встречающейся зависимостью между случайными величинами оказывается линейная корреляционная хависимость, поэтому наличие этой зависимости при исследовании различных случайных величин проверяется в первую очередь.

Рассмотренные нами характеристики связи между случайными величинами, т.е. 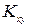и , характеризуют именно степень линейной корреляционной зависимости между случайными величинами Х и У.

При этом они полностью описывают линейную корреляционную зависимость, определяя угол наклона прямых регрессии к координатным осям.

Если же между случайными величинами существуют другие формы или виды вероятностной зависимости, то указанные характеристики для описания этих зависимостей непригодны либо недостаточны.

Когда между двумя случайными существует линейная функциональная зависимость, например,

,

то коэффициент корреляции равен плюс или минус единице. При этом знак коэффициента корреляции совпадает со знаком коэффициента А. Поэтому можно сказать, что величина корреляции по абсолютной величине не превосходит единицы, т.е.

.

На практике часто приходится рассматривать системы более чем двух случайных величин.

Для системы n случайных величин () минимальное число числовых характеристик составят:

_- n математических ожиданий , характеризующих средние значения величин;

_- n дисперсий , характеризующих рассеивание случайных величин;

_- n·(n-1) корреляционных моментов , где , характеризующих попарную корреляцию всех величин, входящих в систему.

Заметим, что есть не что иное, как , т.е.

и т.д.

Все корреляционные моменты, дополненные дисперсиями, можно расположить в виде таблицы (матрицы):

Эта таблица называется корреляционной матрицей случайных величин. Матрица, составленная из коэффициентов корреляции, называется нормированной корреляционной матрицей и имеет вид:

Задача 3.1. Дана корреляционная матрица системы трех случайных величин ():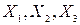

Определить, где степень линейной корреляционной зависимости сильнее – между и или между и .

Решение. Определим средние квадратические отклонения случайных величин и :

Характеристикой степени линейной зависимости является коэффициент корреляции. Поэтому найдем и :

.

Таким образом, связь между случайными величинами и более тесная, чем между и .

Date: 2015-10-18; view: 1144; Нарушение авторских прав