Случйные функции. Цепи Маркова

Основные понятия. Цепи Маркова

Случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, при чем заранее не известно какой именно.

Важным классом случайных функций являются марковские случайные функции – функции, дальнейшее поведение которых зависит только от значения, принятого функцией в настоящий момент, и не зависит от ранее принятых значений. Рассмотрим такие марковские случайные функции X(t), у которых аргумент t принимает дискретное множество значений t₀, t₁,…, t_m и при каждом значении аргумента сама функция принимает одно из значений X₀, X_{1, …,} X_n. Такие марковские случайные функции называют цепями Маркова. Таким образом, цепью Маркова называют последовательность испытаний, в каждом из которых система принимает одно из K состояний полной группы, причем условная вероятность p_i,j(s) того, что при s – м испытании система будет находиться в состоянии j, при условии, что в (s-1) – м испытании она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Однородной называют цепь Маркова, если условная вероятность p_i,j(s) появления событий A_j в s – м испытании при условии, что в предыдущем (s-1) – м испытании наступило событие A_i, не зависит от номера испытания (или, что тоже, от времени). Поэтому вместо p_i,j(s) пишут просто p_i,j.

Вероятностью перехода или переходной вероятностью p_i,j называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично с каким номером) в итоге следующего испытания система перейдет в состояние j. Таким образом, в обозначении p_i,j первый индекс указывает номер предшествующего, а второй – номер последующего состояния. Например, p₁₁ - вероятность «перехода» из первого состояния в первое, p₂₃ - вероятность перехода из второго состояния в третье.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

.

В каждой строке матрицы помещены вероятности событий (переход системы из состояния i в состояние j), которые образуют полную группу. В этой связи сумма вероятностей этих событий равна единице:

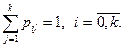
Обозначим через p_i(t_q) вероятность того, что X(t) в момент времени t_q принимает значение X_i. Вектор P (t_q)=(p₀(t_q), p₁(t_q), …, p_k(t_q)) называют вектором вероятностей состояния цепи Маркова в момент времени t_q.

Вектор вероятностей состояний цепи Маркова в момент времени t_q равен произведению вектора вероятностей состояний в момент t_q-1 на матрицу перехода, т.е. P (t_q)= P (t_q-1)*P₁.

Цепь Маркова называется однородной по времени, если вероятность перехода p_i,j из состояния i в состояние j зависит от длины промежутка времени и не зависит от начала отсчета. Однородная цепь Маркова определяется вектором вероятностей состояний в начальный момент P(t₀) и матрицей перехода P₁, т.е.

где - q – я степень матрицы перехода.

Задача 4.1. Цех производит продукцию двух видов X₀ и X_1. Эта продукция поставляется n=100 заказчикам. В некоторый момент времени продукцию X₀ получали n₀=60 заказчиков, а продукцию X₁ получали n₀=40 заказчиков. По истечении месяца оказалось, что из 60 заказчиков, получавших продукцию X_0, m₀₁=12 заказчиков стали получать продукцию X_1, а m₀₀=48, заказчиков – продукцию X₀, а из 40 заказчиков, получавших продукцию X_1, m₁₀=10 заказчиков стали получать продукцию X_0, а m₁₁=30 заказчиков – продукцию X_1.

Определить какая продукция пользуется наибольшим спросом:

а) по истечении месяца; б) по истечении двух месяцев. (Предполагается, что имеет место однородная цепь Маркова).

Решение задачи

а) Вектор вероятностей состояния имеет вид

Матрица перехода имеет вид

По истечении месяца вектор вероятностей состояния будет иметь вид:

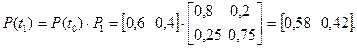
Таким образом, через месяц наибольшим спросом будет пользоваться продукция X_0.

б) Вектор вероятностей через два месяца определяется следующим образом:

Определим на первом этапе При этом,

В таком случае

Поскольку больше , то и через два месяца большим спросом будет пользоваться продукция X_0.

Date: 2015-10-18; view: 454; Нарушение авторских прав