Случайные события

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНИ

НАЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ

–––––––––––––––––––––––––––––––––––––––––––––––––––––––

Г.Г. ШВАЧИЧ, В.И. Христян

Часть 1 (теория вероятностей)

Утверджено на заседании Ученого сонета академии

Как учебное пособие

Днепропетровск НМетАУ 2010

ББК 22.142

Швачич Г.Г., В.И. Христян Теория вероятностей и математическая статистика. Часть 1(теория вероятностей): Учебное пособие. - Днепропетровск: НМетАУ, 2010.- 79 с.

Содержит рабочую программу по теории вероятностей, основной теоретический материал по основним разделам дисциплины. Представлен широкий круг примеров и задач, приведены варианты индивидуальных заданий и вопросы для итогового контроля знаний.

Призначено для студентов инженерных и экономических специальностей.

Печатается в соответствии с авторской редакцией.

Ответственный за выпуск Г.Г.Швачич, канд. техн. наук, проф.

СОДЕРЖАНИЕ

Программа курса «теория вероятностей и математическая статистика» (раздел «теория вероятностей») для студентов экономических специаль-нотей…………………………………………………………………………….5

1. СЛУЧАЙНЫЕ СОБЫТИЯ………………………………………………. 6

1.1. Предмет теории вероятностей……………………………………….6

1.2. Виды случайных событий……………………………………………6

1.3. Непосредственный подсчет вероятностей………………………….7

1.4.Теоремы умножения и сложения вероятностей случайных событий.

Следствия из теорем……………………………………………...….11

1.5.Повторение опытов…………………………………………….……..17

2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ…………………………………….……….20

2.1. Законы распределения и числовые характеристики случайных

величин………………………………………....................................20

2.2. Примеры конкретных распределений………………………….…..29

2.3. Нормированное нормальное распределение (z)……………….…..34

2.4. Распределение К.Пирсона (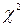)………………………………….…35

2.5. Распределение Стьюдента (t)…………………………………….…35

2.6. Распределение Фишера (F)…………………………………………36

3. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН…………………………….…...40

3.1. Основные понятия. Числовые характеристики системы слу

чайных величин……………………………………………….…….40

4. СЛУЧЙНЫЕ ФУНКЦИИ. ЦЕПИ МАРКОВА………………….………45

4.1. Основные понятия. Цепи Маркова…………………….……….45

5. УКАЗАНИЯ К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ.48

6. ЛИТЕРАТУРА…………………………………………………………...49

7. ЗАДАЧИ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ..50

8. ТАБЛИЦА ВАРИАНТОВ ИНДИВИДУАЛЬНИХ ЗАДАНИЙ………72

Приложение. ТАБЛИЦЫ функции Гауса и функции Лапласа……...…74

ПРОГРАММА КУРСА «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА» (РАЗДЕЛ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ») ДЛЯ СТУДЕНТОВ ЭКОНОМИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ

I. СЛУЧАЙНЫЕ СОБЫТИЯ.

1.1. Предмет теории вероятностей. Основные понятия и определения. Классическое определение вероятности. Геометрическое определение вероятности. Статистическое определение вероятности.

1.2. Операции над событиями и отношения между ними. Теоремы умножения и сложения вероятностей случайных событий. Следствия из теорем.

1.3. Повторение опытов. Формулы Бернулли и Пуассона. Предельные теоремы Муавра-Лапласса.

II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

2.1.Определение случайной величины. Формы законов распределе- ния. Числовые характеристики случайных величин.

2.2. Дискретные и непрерывные распределения. Примеры распределений: биномиальное, пуассоновское, равномерное, показательное, нормальное. Распределения, связанные с нормальным.

III. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН.

3.1.Понятие системы случайных величин. Корреляционный момент. Коэффициент корреляции. Корреляционная матрица. Нормированная матрица.

IV. ЦЕПИ МАРКОВА.

4.1. Случайные функции. Цепи Маркова. Вероятности перехода. Матрица перехода. Равенство Маркова.

СЛУЧАЙНЫЕ СОБЫТИЯ

Date: 2015-10-18; view: 353; Нарушение авторских прав