Производственные функции выпуска продукции

Производственная функция алгебраически связывает входы и выходы производственной системы, т.е. определяет связь между затратами факторов производства и выпуском продукции. Производственные функции для реальных производственных систем оцениваются с помощью статистических методов обработки эмпирических данных.

Производственная функция описывает наиболее эффективные производственные процессы. При этом менее эффективные производственные процессы исключаются из рассмотрения.

Производственные функции могут быть определены для производственных систем различных масштабов – от производственного участка до мировой экономики. Каждая производственная система характеризуется собственной производственной функцией.

Производственные функции используются для анализа свойств системы и управления производством. С помощью производственных функций можно оценить эффективность функционирования системы и использования отдельных производственных факторов, определить возможности и последствия замещения одних факторов производства другими, изучить воздействие управленческих и технологических инноваций на производственные процессы.

Связь между количеством произведённого продукта и количествами затраченных факторов в виде производственной функции обычно математически представляется с помощью непрерывно дифференцируемой функции, имеющей первые и вторые производные.

Часто рассматриваются факторы производства в виде набора двух агрегированных товаров – капитала K и труда L. Это упрощает процесс моделирования, улучшает точность оценки параметров модели по имеющимся эмпирическим данным на основе эконометрических методов и даёт возможность графического представления набора товаров в виде точки на плоскости.

При анализе производства с помощью набора затрат факторов в форме капитал – труд производственная функция системы связывает количество полученного продукта Y с затратами факторов труда L и капитала K за фиксированный период времени соотношением

. (3.1)

Рассмотрим основные свойства производственных функций для случая двух факторов производства. Производственная функция называется неоклассической, если она обладает следующими четырьмя свойствами.

1.

2. / > , / > .

3. / < , / < .

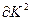4.

Первое свойство неоклассической функции показывает, что при отсутствии затрат одного из факторов производства получаем нулевой продукт. В нашем случае это означает, что невозможно произвести никакой продукт без затрат труда или капитала.

Второе свойство неоклассической функции показывает, что при увеличении затрачиваемых факторов производства до определённого уровня количество производимого продукта увеличивается.

Третье свойство неоклассической функции связано с её вогнутостью. Свойство вогнутости производственной функции математически выражает закон убывания предельной эффективности производства продукта при увеличении затрат факторов, т.е. при увеличении затрат труда и капитала эффективность их преобразования в продукт уменьшается.

Четвёртое свойство неоклассической функции требует, чтобы функция обладала свойством линейной однородности, т.е. чтобы при одновременном изменении количества всех затрат в раз количество произведённого продукта в системе тоже изменилось в раз. Данное свойство является следствием линейности технологических процессов.

Свойство линейной однородности неоклассической производственной функции двух переменных позволяет преобразовать её в функцию одной переменной и уменьшить число независимых аргументов до одной переменной. Для этого запишем производственную функцию в виде (3.1) и преобразуем, используя её линейную однородность

(3.2)

Разделив обе части этого уравнения на L, получим

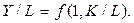
Назовём фондовооружённостью k отношение затрат капитала к затратам труда, а средней производительностью труда отношение произведённого продукта к затратам труда. Тогда полученное уравнение для модифицированной производственной функции, связывающей среднюю производительность труда y и фондовооружённость k, примет вид

(3.3)

Для неоклассической линейно-однородной модифицированной производственной функции f справедливы следующие соотношения:

´ ´´

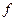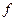Рассмотрим основные показатели эффективности производства на примере неоклассической производственной функции. Назовём средним продуктом соответствующего фактора производства отношение количества произведённого продукта к количеству затраченного фактора за фиксированный момент времени. Так, средняя фондоотдача и средняя производительность труда 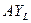определятся как

Средняя фондоотдача – это средний продукт капитала, равный среднему количеству произведённого продукта единицей капитала, а средняя производительность труда – это средний продукт труда, равный среднему количеству произведённого продукта единицей труда.

Влияние малого изменения величины потребляемого фактора определяется через понятие предельного продукта фактора. Чем меньше предельный продукт фактора, тем больше должно быть увеличение затрат фактора, которое вызывает увеличение производства на одну единицу продукта.

Увеличение затрат фактора приводит к уменьшению среднего продукта фактора. Это происходит в результате вогнутости производственной функции.

Предельный продукт фактора – это дополнительный продукт, произведённый системой при затратах дополнительной единицей соответствующего фактора. Математически предельный продукт фактора определяется как первая частная производная продукта по затратам соответствующего фактора.

В случае двух факторов предельный продукт капитала (предельная фондоотдача) и предельный продукт труда (предельная производительность труда) определяются из соотношений

;

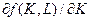С увеличением затрат фактора предельный продукт монотонно уменьшается.

Из вогнутости производственной функции следует, что средний продукт фактора всегда больше предельного продукта фактора.

Введём понятие эластичности продукта по фактору. Коэффициент эластичности или просто эластичность продукта по фактору показывает изменение производимого продукта, выраженное в процентах, при изменении фактора на один процент.

В случае двух факторов вводятся понятия коэффициентов эластичности выпуска по фондам и по труду . Определяются они соответственно из выражений

;

Из этих соотношений следует, что предельный продукт фактора равен среднему продукту, умноженному на соответствующий коэффициент эластичности;

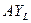; . (3.4)

Введение коэффициентов эластичности по факторам производства позволяет вычислить изменение выпуска производимого продукта при одновременном изменении объёмов затрачиваемых факторов.

Раскладывая производственную функцию в ряд Тейлора имеем

причём правая часть равенства высчитывается в точке Воспользовавшись соотношениями (8.4) получим

Date: 2015-10-18; view: 1374; Нарушение авторских прав