
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм Евклида
|
|
1-й шаг. Делим а на b 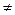 0. Если а
0. Если а  b, то (а, b) = b по лемме 8.2. Если а = bq0 + r1, то (а, b) = (b, r 1).
b, то (а, b) = b по лемме 8.2. Если а = bq0 + r1, то (а, b) = (b, r 1).
2-й шаг. Делим b на r1. Если b  r1, то (b, r1) = r1. Если b = r1q1 + r2, то (b, r1) = (r1, r2).
r1, то (b, r1) = r1. Если b = r1q1 + r2, то (b, r1) = (r1, r2).
3-й шаг. Делим r1 на r2 b и т.д.
Лемма 8.4. Алгоритм Евклида состоит из конечного числа шагов.
Действительно, остатки, получаемые в процессе деления убывают и являются натуральными числами | b | < r1 < r2 < …, поэтому не более, чем за | b | шагов получим остаток равный нулю, т.е. (rn-1, rn) = rn и тогда (rn-1, rn) = rn.
Теорема 8.5 (о нахождении НОД(а, b) с помощью алгоритма Евклида). Последнийотличный от нуля остаток валгоритме Евклида является наибольшим общим делителем целых чисел а и b (а 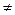 0, b
0, b 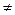 0).
0).
Доказательство. Применим к числам a и b алгоритм Евклида:
а = bq0 + r1, 0 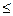 r1 < b
r1 < b
b = r1q + r2, 0 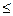 r2 < r1
r2 < r1
………………………….
rn-2 = rn-1 ∙ qn-1 + rn, 0 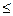 rn < rn-1
rn < rn-1
rn-1 = rn ∙ qn + 0
Из первого равенства по лемме 8.3 будем иметь (а, b) = (b, r1). Из второго равенства алгоритма Евклида по лемме 8.3 будем иметь: (b, r1) = (r1, r2) и т.д.
Из последнего равенства (rn-1, rn) = rn.
Итак, (а, b) = rn.
Пример. ВычислимНОД (154, 48) с помощью алгоритма Евклида.
_ 154 | 48
144 3
_ 48 | 10
40 4
_10 | 8
8 1
_ 8 | 2
8 4
Процесс деления можно записывать в виде последовательности равенств деления с остатком, называемой последовательностью Евклида.
154 = 48 ∙ 3 + 10
48 = 10 ∙ 4 +8
10 = 8 ∙ 1 + 2
8 = 2 ∙ 4
Итак, НОД (154, 48) = 2.
Следствие 1 (о линейном разложении НОД(a, b)). Наибольший общий делитель НОД(a, b) любых целых чисел a 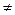 0, b
0, b 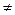 0 можно представить в виде линейной комбинации чисел a и b c целыми коэффициентами u и v: НОД (a, b) = u ∙ a + v ∙ b (1)
0 можно представить в виде линейной комбинации чисел a и b c целыми коэффициентами u и v: НОД (a, b) = u ∙ a + v ∙ b (1)
Определение 8.3. Представление (1) называется линейным разложением наибольшего общего делителя чисел a и b.
Пример. Найдем линейное представление НОД(154, 48). Воспользуемся последовательностью Евклида из предыдущего примера, выразим остатки: 2 = 10 + 8 ∙ (-1), 8 = 48 + 10 ∙ (-4), 10 = 154 + 48 ∙ (-3). Подставим в первое равенство выражение 8 из второго, затем для 10 из третьего, получаем: 2 = 10 + [48 + 10∙ (-4)] ∙ (-1) = 48 ∙ (-1) + 10 ∙ 5 = 48 ∙ (-1) + [154 + 48 ∙ (-3)] ∙ 5 = 154 ∙ 5 + 48 ∙ (-16).
Итак, 154 ∙ 5 + 48 ∙ (-16) = 2 – линейное разложение (154, 48).
Date: 2015-10-18; view: 568; Нарушение авторских прав