
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Отношение делимости в кольце Z и его свойства
|
|
Определение. 7.1. Целое число а делится на целое число b 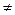 0, если
0, если
 q
q  Z а = bq.
Z а = bq.
Обозначается а  b и читается “ a делится на b ”, а также b | a и читается “ b делит а ”.
b и читается “ a делится на b ”, а также b | a и читается “ b делит а ”.
а – делимое, b – делитель, q – частное.
Используется и другое обозначение:
Свойства:
10. Отношение делимости рефлексивно на множестве ненулевых целых чисел (т.е.  а
а  Z \ {0} а
Z \ {0} а  а), т. к.
а), т. к.  1
1  Z: а = а · 1.
Z: а = а · 1.
20 Отношение делимости транзитивно на множестве целых чисел:
(т.е.  а, b, c
а, b, c  Z а
Z а  b
b 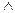 b
b  c
c  a
a  c), т.к. (а
c), т.к. (а  b)
b) 
 q1
q1  Z: а = bq1, кроме того, (b
Z: а = bq1, кроме того, (b  c)
c) 
 q2
q2  Z: b= cq2
Z: b= cq2  а = cq2q1 = cq2
а = cq2q1 = cq2  (а
(а  c).
c).
30 Отношение делимости не антисимметрично на множестве целых чисел, т.к.  а, b
а, b  Z (а
Z (а  b
b 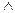 b
b  а)
а)  [(a = b)
[(a = b) 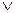 (a = - b)].
(a = - b)].
40 Отношение делимости антисимметрично на множестве натуральных чисел (т.е.  а, b
а, b  N а
N а  b
b 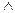 b
b  а
а  а = b), т.к. если b = a × n, a = b × m, то m, n Î N, и b = (b× m) × n = = b× (m × n), т.е. m × n = 1, и m = n = 1, а значит, а = b.
а = b), т.к. если b = a × n, a = b × m, то m, n Î N, и b = (b× m) × n = = b× (m × n), т.е. m × n = 1, и m = n = 1, а значит, а = b.
Следовательно, отношение делимости не является отношением эквивалентности, а будет отношением частичного порядка на множестве N.
50. Если a  b, то для любого ненулевого целого c выполнено aс
b, то для любого ненулевого целого c выполнено aс  b.
b.
Действительно, если a  b, то b= a × q для некоторого целого q, тогда
b, то b= a × q для некоторого целого q, тогда
b× c = a× (q× c), следовательно, aс  b
b
60. Если a  b, то (± a)
b, то (± a)  (± b) при любой независимой друг от друга расстановке знаков у чисел a и b.
(± b) при любой независимой друг от друга расстановке знаков у чисел a и b.
Свойство 60 является следствием свойства 50 и определения делимости.
70. Если a 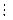 b1, …, bn
b1, …, bn  a, то (b1 + … + bn)
a, то (b1 + … + bn)  a.
a.
8 0. Если b1 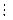 a, …, bn
a, …, bn 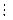 a, то для любых целых r1 , …, rn выполнено a (b1 × r1 + …+ bn × rn )
a, то для любых целых r1 , …, rn выполнено a (b1 × r1 + …+ bn × rn ) 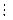 a.
a.
Свойство 8 0 является следствием свойств 60 и 70.
Замечание 1. Запись 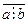 означает, что а не делится на b.
означает, что а не делится на b.
Определение. 7.2. Целое число а делится на b  Z, b
Z, b 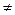 0 с остатком, если
0 с остатком, если  q, r
q, r  Z: а = bq + r, где 0 < r < | b |, a – делимое, b – делитель, q – неполное частное, r – остаток.
Z: а = bq + r, где 0 < r < | b |, a – делимое, b – делитель, q – неполное частное, r – остаток.
Замечание 2. Из определения следует, что остаток всегда число неотрицательное.
Примеры. Разделить с остатком а на b, если: а) при а = 53 на b= 5, получим: 53 = 5 · 10 + 3 (т.е. неполное частное q = 10, остаток r = 3).
б ) при а = -53 на b = 5, получим: -53 = 5 · (-11) + 2 (q = -11, r = 2)
в) при а= -53 на b = – 5, получим: -53 = -5 · 11 + 2.
г ) при а = 53 на b = – 5, получим: 53 = (-5) · (-10) + 3.
Теорема 7.1 (о делении с остатком). Для любых целых чисел a, b  0 однозначно определены частное q и остаток r от деления a на b т.е.
0 однозначно определены частное q и остаток r от деления a на b т.е.
" a Î Z " b Î Z \ {0} $! q, r Î Z a = bq + r Ù 0 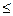 r < |b|).
r < |b|).
Доказательство.
I. Покажем возможность деления.
1. Пусть a  0, b > 0. Докажем существование деления с остатком числа a на число b методом математической индукции по числу a.
0, b > 0. Докажем существование деления с остатком числа a на число b методом математической индукции по числу a.
a) Если a = 0, то 0 = b× 0 + 0 (имеем: q = 0, r = 0) и в этой ситуации возможность деления с остатком показано.
б) Пусть а > 0 и bq – наибольшее кратное числа b, которое не превосходит а, тогда bq 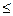 a< b (q + 1), следовательно, 0
a< b (q + 1), следовательно, 0 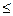 a – bq < b или 0
a – bq < b или 0 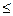 a – bq < | b |.
a – bq < | b |.
Положим, что а – bq = r, тогда получим что, а = bq + r, где 0 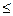 r
r 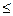 | b |.
| b |.
Итак, для неотрицательных целых чисел a и b существование деления с остатком доказано.
2. Пусть a > 0, b < 0. Тогда |b| > 0 и согласно п.1 существует формула деления с остатком для положительного числа а на положительное число | b |, поэтому a = | b |× q + r, где 0 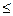 r
r 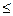 | b |. Тогда a = b × (– q) + r – искомая формула деления с остатком а на b.
| b |. Тогда a = b × (– q) + r – искомая формула деления с остатком а на b.
3. Пусть a < 0, b > 0, тогда (– а) > 0 и согласно п.1 (– a) = b× q + r, где 0 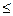 r < | b |. При r = 0 данная формула принимает вид: а = b× (– q) + 0. При r > 0 имеем a = b× (– q) – r = b× (– q – 1) + (b – r), причём 0 < b – r < b, или 0 < b – r < | b | т.е. (– q – 1), (b – r) – искомые частное и остаток соответственно.
r < | b |. При r = 0 данная формула принимает вид: а = b× (– q) + 0. При r > 0 имеем a = b× (– q) – r = b× (– q – 1) + (b – r), причём 0 < b – r < b, или 0 < b – r < | b | т.е. (– q – 1), (b – r) – искомые частное и остаток соответственно.
4. Пусть a < 0, b < 0. Тогда (–b) > 0 и согласно п.3 существует формула деления с остатком для отрицательного числа а на положительное число (– b), поэтому a = (– b) × q′ + r′, где 0 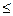 r′
r′ 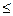 | b | (согласно п. 3 имеем: q′= (– q – 1), r ′ = (b – r)) или a = b × (– q′ ) + r′,
| b | (согласно п. 3 имеем: q′= (– q – 1), r ′ = (b – r)) или a = b × (– q′ ) + r′,
II. Докажем единственность существования частного и остатка от деления а на b.
Предположим противное.
Пусть a = bq1+ r1, 0 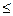 r1<| b| и a = bq2 + r2, 0
r1<| b| и a = bq2 + r2, 0 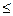 r2< |b|. Тогда
r2< |b|. Тогда
b (q1 – q2) = (r1 – r2) < | b |  (r1 – r2)
(r1 – r2)  b, а т. к. 0
b, а т. к. 0 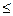 | r1 – r2 | < | b |
| r1 – r2 | < | b | 
 (r1 – r2) = 0
(r1 – r2) = 0  (r2 = r1)
(r2 = r1)  b (q1 – q2) = 0, b
b (q1 – q2) = 0, b 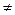 0
0  q1 = q2.
q1 = q2.
МЕТОДИКА 17. Тема урока: «Делители и кратные».
Обучающие цели: ввести понятие делителя и кратного натурального числа; отрабатывать умение находить делители и кратные данного натурального числа.
Развивающие цели: развитие мышления, совершенствование устных и письменных вычислительных навыков, развитие математической речи учащихся.
Воспитательные цели: воспитание интереса к математике, воспитание таких качеств личности как аккуратность, последовательность, настойчивость и т.д.
Тип урока: урок изучения нового материала.
Date: 2015-10-18; view: 1631; Нарушение авторских прав