Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Задание №3. Тема. Множественная линейная регрессия

⇐ ПредыдущаяСтр 17 из 17

Тема. Множественная линейная регрессия.

 

Экономический показатель Y зависит от трех факторов. На основе статистических данных за 15 периодов построить корреляционную матрицу. Используя - критерий, с надежностью р=0,95 оценить наличие мультиколлинеарности. Если существует общая мультиколлинеарность, то используя t-статистику с надежностью , обнаружить пары факторов, между которыми существует мультиколлинеарность. Если такие пары существуют, то один из факторов этой пара исключить из рассмотрения. Используя сервис: математика/матрицы, найти оценки параметров линейной регрессии. Результат полученных оценок проверить, используя сервис: статистика/линейн.

Используя F-критерий с надежностью , проверить статистическую значимость коэффициента детерминации (оценить адекватность принятой математической модели статистическим данным на основе критерия Фишера).

Если математическая модель с заданной надежностью адекватная статистическим данным, то используя t-статистику с надежностью оценить значимость параметров регрессии, найти значения прогноза показателя для заданных значений факторов (блок a18:c18) (табл. 3.1), его доверительный интервал с надежностью , частныеі коэффициенты эластичности для точки прогноза. На основе полученных расчетов сделать экономический анализ.

 

ТАБЛИЦА 3

Вариант 1 Вариант2 Вариант 3 Вариант 4
Х1 Х2 ХЗ Y X1 Х2 ХЗ Y XI Х2 ХЗ Y XI X2 X3 Y
2,31 10,1 6,32 7,63 2,12 9,97 6,28 7,45 2,41 10,3 6,32 7,73 2,37 10,3 6,4 7,73
4,67 11,7 7,73 10,7 4,4 11,4 7,64 10,5 4,78   7,79 10,94 4,77 11,9 7,88 10,9
6,17 13,9 8,48 11,5 6,16 13,6 8,25 11,3 6,26 13,9 8,57 11,82 6,24 13,9 8,5 11,5
8,7 14,4 8,69 13,4 8,69 14,2 8,61 13,3 8,95 14,5 8,83 13,59 8,7 14,6 8,86 13,5
10,7 15,1 10,5   10,5 14,9 10,2 16,9 10,8 15,2 10,55 17,15 10,8 15,3 10,5 17,1
13,5 17,1 10,5 18,8 13,4   10,4 18,6 13,6 17,4 10,59 18,81 13,6 17,3 10,5 18,8
16,2 18,9 11,6 21,1   18,8 11,5 20,9 16,4   11,83 21,26 16,3   11,7 21,2
18,3 20,3 13,8 23,4 18,2 20,3 13,7 23,3 18,6 20,5 13,83 23,38 18,4 20,5   23,5
21,2 21,7 13,7 27,5 20,9 21,5 13,6 27,2 21,5   13,97 27,62 21,3 21,9 13,9 27,5
22,7 22,4 14,4 27,1 22,7 22,2 14,4   22,8 22,5 14,55 27,18 22,7 22,6 14,6 27,2
25,1 22,5 14,1 29,6 24,9 22,4   29,6 25,2 22,6 14,17 29,87 25,2 22,6 14,2 29,7
26,1 24,7 16,5 32,5   24,5 16,5 32,2 26,3 24,9 16,64 32,64 26,3 24,8 16,6 32,7
27,5 24,8   31,8 27,3 24,8 14,8 31,7 27,6   15,07 32,01 27,7 24,8   31,8
29,9   15,3 35,2 29,7 24,9 15,1 35,1 30,2 25,2 15,38 35,25   25,1 15,3 35,2
32,1   15,6 37,1 31,8   15,6 36,8 32,2 26,2 15,72 37,14 32,3 26,1 15,8 37,1
33,7 27,4 17,2 38,9 33,7 27,3 17,1 38,7 33,9 27,6 17,27 38,96 33,9 27,6 17,3  
35,8 28,9 17,5 ? 35,6 28,8 17,4 ?     17,56 ?   29,1 17,5 ?

 

Вариант 5 Вариант 6 Вариант 7 Вариант 8
XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y
2,25 9,9 6,09 7,49 2,61 10,4 6,61 7,72 2,61 10,3 6,71 7,95 2,4 11,27 6,78 8,61
4,42 11,5 7,49 10,6 4,89 11,8 7,74 10,8 4,97   8,14 10,8 5,66 12,48 8,49 11,33
6,08 13,7 8,46 11,4 6,24 14,1 8,62   6,55   8,95 11,7 6,87 14,11 9,46 12,48
8,65 14,3 8,59 13,2 9,01 14,6 8,83 13,7 9,16 14,6 8,83 13,5 9,52 14,64 9,44 14,37
10,6 14,9 10,4   10,8 15,2 10,7   10,7 15,2   17,4 11,57 16,17 10,82 17,43
13,3   10,5 18,6 13,5 17,4 10,7 18,8 13,9 17,3 10,9 19,1 13,73 17,47 11,01 19,5
  18,8 11,7 21,1 16,3 19,2 11,8 21,3 16,3 19,2 11,8 21,4 16,87 19,85 12,16 21,22
18,3 20,1 13,6 23,2 18,6 20,6 13,8 23,7 18,7 20,4 14,1 23,9 18,73 21,43 14,46 23,84
21,1 21,7 13,7 27,4 21,5   13,7 27,6 21,3 22,2 14,1 27,9 22,16 22,12 13,98 27,8
22,7 22,3 14,3 27,1   22,7 14,6 27,5 22,9 22,8 14,6 27,3 23,33 22,98 14,72 27,82
  22,4   29,4 25,2 22,7 14,1 29,7 25,1 22,6 14,4   25,84 22,61 14,58 30,01
  24,5 16,3 32,4 26,4 24,8 16,7 32,8 26,3 24,9 16,6 32,8 26,69 25,03 17,07 33,32
27,3 24,8 14,8 31,7 27,6 24,8 15,1   27,7 24,9 15,5 31,7 27,78 25,16 15,39 31,87
29,8   15,1 35,2 30,2 25,2 15,4 35,2   25,3 15,4 35,2 30,86 26,05 15,95 35,35
31,9 25,9 15,5 37,1 32,3 26,2 15,8 37,3 32,1 26,2   37,3 32,87 26,44 16,37 37,5
33,6 27,4   38,7 33,8 27,7 17,4 39,2 33,7 27,6 17,6   34,65 28,09 17,94 39,91
35,7 28,8 17,3 ?   29,2 17,8 ? 36,3 29,2   ? 36,25 29,76 18,44 ?

 


 

Вариант 9 Вариант 10 Вариант 11 Вариант 12
XI X2 X3 Y X1 X2 X3 Y XI X2 X3 Y X1 X2 X3 Y
1,43 9,18 6,17 7,29 3,18 10,9 6,94 8,5 1,49 10,1 5,97 7,54 0,95 8,71 4,67 5,94
3,92 10,9 7,7 9,79 5,76 12,7 8,2 11,7 3,65 10,5 6,62 10,4 2,82 10,89 6,16 10,2
5,49 13,3 8,43 11,3 7,26 14,4 9,03 12,1 6,11 13,1 7,92 11,5 6,09 13,54 7,18 10,22
8,17 13,9 8,12 12,4 8,95   9,37 14,1 3,59   8,17 12,4 7,36 12,56 6,81 12,4
9,68 14,5 10,4   11,4 16,2 10,6   9,73 15,1   15,9 10,28 13,5 9,87 15,64
13,4 16,7 10,4 18,3 14,6 18,1 10,6 19,2 12,5 16,5   18,2 11,97 16,69 8,58 18,23
15,9     20,9 16,9 19,7 12,2 21,3 15,6 17,7 11,6 20,3 15,08 18,84 10,22 19,34
  19,5 13,3 22,7 18,4 21,1   23,5   19,8 13,4 23,3 16,43 19,59 12,72 23,28
20,7 21,5 12,7 27,1 21,8 22,5 13,8 27,7 20,4 20,6 13,3 27,3 19,59 20,15 12,39 25,8
22,7 21,6 14,2 26,4 23,9 22,6   27,2 21,7 22,1 13,8 26,3 22,44 20,79 13,12 25,47
24,3 21,6 13,5 29,4   22,7 14,5 30,3 23,9 22,4 13,6 29,5 24,53 20,57 12,58 27,72
25,6 24,5 15,8 32,4 26,9 25,8 17,6 33,1   23,8 15,5 32,3 24,56 23,28 16,15 31,4
27,1   14,5 31,5 28,7 25,6 15,6 32,2 26,5 24,3 14,5 31,8 27,39 24,47 13,3 31,67
29,2 24,4 15,1 34,9 30,4   16,2 35,4 29,3 24,3 14,8 34,7 29,41   14,73 33,68
31,1   15,3 36,3 32,7 26,4 16,6 37,2 31,6 25,7 14,6   31,82 24,87 14,94 36,97
33,3 27,1 16,7 38,4 33,9 28,5 17,3 39,6 32,6 27,4   38,3 33,13 26,17 16,81 37,22
35,6 28,1 16,6 ? 36,5 29,1 18,6 ? 35,7 28,1 16,5 ? 35,2 28,3 16,57 ?

 


Вариант 13 Вариант14 Вариант 15 Вариант 16
Х1 Х2 ХЗ Y X1 Х2 ХЗ Y XI Х2 ХЗ Y XI X2 X3 Y
5,79 13,58 9,795 11,107 5,6 13,45 9,76 10,93 5,89 13,73 9,8 11,21 5,85 13,75 9,88 11,21
8,15 15,18 11,209 14,18 7,88 14,91 11,12 13,96 8,26 15,43 11,27 14,42 8,25 15,35 11,36 14,33
9,65 17,38 11,959 15,01 9,64 17,09 11,73 14,73 9,74 17,35 12,05 15,3 9,72 17,34 11,98 15,02
12,18 17,88 12,171 16,88 12,17 17,71 12,09 16,81 12,43   12,31 17,07 12,18 18,1 12,34  
14,18 18,58 13,98 20,5 13,95 18,41 13,69 20,38 14,23 18,66 14,03 20,63 14,27 18,74 13,99 20,61
16,98 20,58   22,23 16,89 20,52 13,91 22,05 17,05 20,89 14,07 22,29 17,08 20,77 14,01 22,23
19,68 22,38 15,06 24,62 19,46 22,3 15,02 24,39 19,91 22,49 15,31 24,74 19,79 22,52 15,22 24,63
21,78 23,78 17,25 26,85 21,72 23,78 17,21 26,8 22,03   17,31 26,86 21,88 23,93 17,44 26,97
24,68 25,18 17,18 30,93 24,37 24,96 17,12 30,64 24,93 25,5 17,45 31,1 24,73 25,42 17,34 30,98
26,18 25,88 17,91 30,61 26,14 25,7 17,89 30,48 26,23 26,01 18,03 30,66 26,15 26,03 18,08 30,64
28,58 25,98 17,55 33,09 28,39 25,89 17,46 33,07 28,67 26,12 17,65 33,35 28,63 26,04 17,72 33,21
29,58 28,18 19,94   29,51 27,93 19,93 35,72 29,73 28,37 20,12 36,12 29,75 28,27 20,07 36,19
30,98 28,28 18,5 35,28 30,73 28,23 18,31 35,19 31,11 28,5 18,55 35,49 31,18 28,3 18,51 35,31
33,38 28,48 18,75 38,66 33,22 28,37 18,54 38,58 33,64 28,67 18,86 38,73 33,48 28,59 18,82 38,66
35,58 29,48 19,06 40,55 35,28 29,43 19,09 40,25 35,68 29,63 19,2 40,62 35,73 29,59 19,32 40,6
37,18 30,88 20,69 42,33 37,14 30,75 20,62 42,18 37,42 31,08 20,75 42,44 37,33 31,06 20,78 42,45
39,28 32,38 20,95 ? 39,05 32,28 20,87 ? 39,48 32,5 21,04 ? 39,44 32,57 20,96 ?

 

Вариант 17 Вариант 18 Вариант 19 Вариант 20
XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y
5,73 13,38 9,57 10,97 6,09 13,83 10,09 11,2 6,09 13,8 10,19 11,43 5,88 14,75 10,26 12,09
7,9 15,02 10,97 14,12 8,37 15,26 11,22 14,25 8,45 15,44 11,62 14,23 9,14 15,96 11,97 14,81
9,56 17,21 11,94 14,92 9,72 17,57 12,1 1189,48 10,03 17,44 12,43 15,14 10,35 17,59 12,94 15,96
12,13 17,74 12,07 16,72 12,49 18,12 12,31 17,21 12,64 18,1 12,31 16,97   18,12 12,92 17,85
14,12 18,39 13,91 20,47 14,27 18,65 14,16 20,52 14,16 18,66 14,43 20,92 15,05 19,65 14,3 20,91
16,77 20,5   22,05 17,01 20,9 14,14 22,28 17,41 20,82 14,4 22,53 17,21 20,95 14,49 22,98
19,43 22,32 15,13 24,55 19,8 22,72 15,26 24,76 19,75 22,69 15,23 24,9 20,35 23,33 15,64 24,7
21,73 23,54 17,03 26,71 22,08 24,08 17,26 27,18 22,22 23,84 17,53 27,33 22,21 24,91 17,94 27,32
24,58 25,19 17,15 30,85 24,96 25,52 17,22 31,11 24,79 25,69 17,57 31,4 25,64 25,6 17,46 31,28
26,15 25,79 17,81 30,6 26,5 26,17 18,04 30,93 26,36 26,32 18,08 30,75 26,81 26,46 18,2 31,3
28,47 25,87 17,43 32,9 28,65 26,13 17,57 33,19 28,61 26,11 17,86 33,52 29,32 26,09 18,06 33,49
29,48 27,98 19,82 35,91 29,88 28,31 20,14 36,28 29,76 28,41 20,05 36,31 30,17 28,51 20,55 36,8
30,82 28,24 18,29 35,22 31,1 28,3 18,6 3184,48 31,19 28,42 18,99 35,17 31,26 28,64 18,87 35,35
33,23 28,47 18,61 38,64 33,67 28,65 18,9 38,7 33,49 28,75 18,92 38,69 34,34 29,53 19,43 38,83
35,35 29,42 18,94 40,55 35,73 29,7 19,25 40,74 35,56 29,66 19,48 40,75 36,35 29,92 19,85 40,98
37,03 30,83 20,44 42,22 37,24 31,2 20,88 42,68 37,22 31,09 21,07 42,47 38,13 31,57 21,42 43,39
39,19 32,31 20,73 ? 39,45 32,63 21,25 ? 39,79 32,71 21,45 ? 39,73 33,24 21,92 ?

 


Вариант 21 Вариант 22 Вариант 23 Вариант 24
XI X2 X3 Y X1 X2 X3 Y XI X2 X3 Y X1 X2 X3 Y
4,91 12,66 9,65 10,77 6,66 14,33 10,42 11,98 4,97 13,6 9,45 11,02 4,43 12,19 8,15 9,42
7,4 14,42 11,18 13,27 9,24 16,14 11,68 15,15 7,13 14,02 10,1 13,84 6,3 14,37 9,64 13,68
8,97 16,78 11,91 14,74 10,74 17,83 12,51 15,59 9,59 16,57 11,4 14,94 9,57 17,02 10,66 13,7
11,65 17,37 11,6 15,9 12,43 18,52 12,85 17,57 7,07 17,51 11,65 15,84 10,84 16,04 10,29 15,88
13,16 17,97 13,89 19,52 14,92 19,68 14,03 21,49 13,21 18,61 13,49 19,36 13,76 16,98 13,35 19,12
16,9 20,21 13,87 21,82 18,07 21,61 14,05 22,69 15,97 19,99 13,49 21,69 15,45 20,17 12,06 21,71
19,4 21,45 14,48 24,42 20,39 23,21 15,66 24,81 19,06 21,21 15,09 23,82 18,56 22,32 13,7 22,82
21,52 22,93 16,8 26,22 21,88 24,57 17,5 27,02 21,51 23,28 16,91 26,82 19,91 23,07 16,2 26,76
24,17 24,97 16,2 30,57 25,32 25,95 17,25 31,2 23,91 24,03 16,81 30,82 23,07 23,63 15,87 29,28
26,16 25,08 17,7 29,91 27,36 26,04 18,49 30,64 25,19 25,56 17,26 29,78 25,92 24,27 16,6 28,95
27,81 25,12 16,99 32,87 29,46 26,16 17,99 33,74 27,36 25,84 17,12 32,99 28,01 24,05 16,06 31,2
29,12 27,96 19,31 35,85 30,33 29,24 21,1 36,57 29,48 27,32 18,95 35,73 28,04 26,76 19,63 34,88
30,62 27,5 18,02   32,19 29,11 19,07 35,7 30,32 27,77 18,45 35,26 30,87 27,95 16,78 35,15
32,7 27,9 18,54 38,37 33,86 28,48 19,71 38,9 32,74 27,81 18,23 38,19 32,89 26,48 18,21 37,16
34,57 29,44 18,8 39,81 36,14 29,84 20,11 40,69 35,03 29,21 18,07 39,44 35,3 28,35 18,42 40,45
36,82 30,53 20,13 41,83 37,36 32,02 20,76 43,12 36,09 30,86 20,5 41,81 36,61 29,65 20,29 40,7
39,12 31,6 20,03 ? 40,02 32,61 22,07 ? 39,14 31,62 19,93 ? 38,68 31,78 20,05 ?

 

Вариант 25 Вариант 26 Вариант 27 Вариант 28
Х1 Х2 ХЗ Y X1 Х2 ХЗ Y XI Х2 ХЗ Y XI X2 X3 Y
5,06 12,85 9,065 10,377 4,87 12,72 9,03 10,2 5,16   9,07 10,48 5,12 13,02 9,15 10,48
7,42 14,45 10,479 13,45 7,15 14,18 10,39 13,23 7,53 14,7 10,54 13,69 7,52 14,62 10,63 13,6
8,92 16,65 11,229 14,28 8,91 16,36     9,01 16,62 11,32 14,57 8,99 16,61 11,25 14,29
11,45 17,15 11,441 16,15 11,44 16,98 11,36 16,08 11,7 17,27 11,58 16,34 11,45 17,37 11,61 16,27
13,45 17,85 13,25 19,77 13,22 17,68 12,96 19,65 13,5 17,93 13,3 19,9 13,54 18,01 13,26 19,88
16,25 19,85 13,27 21,5 16,16 19,79 13,18 21,32 16,32 20,16 13,34 21,56 16,35 20,04 13,28 21,5
18,95 21,65 14,33 23,89 18,73 21,57 14,29 23,66 19,18 21,76 14,58 24,01 19,06 21,79 14,49 23,9
21,05 23,05 16,52 26,12 20,99 23,05 16,48 26,07 21,3 23,27 16,58 26,13 21,15 23,2 16,71 26,24
23,95 24,45 16,45 30,2 23,64 24,23 16,39 29,91 24,2 24,77 16,72 30,37   24,69 16,61 30,25
25,45 25,15 17,18 29,88 25,41 24,97 17,16 29,75 25,5 25,28 17,3 29,93 25,42 25,3 17,35 29,91
27,85 25,25 16,82 32,36 27,66 25,16 16,73 32,34 27,94 25,39 16,92 32,62 27,9 25,31 16,99 32,48
28,85 27,45 19,21 35,27 28,78 27,2 19,2 34,99   27,64 19,39 35,39 29,02 27,54 19,34 35,46
30,25 27,55 17,77 34,55   27,5 17,58 34,46 30,38 27,77 17,82 34,76 30,45 27,57 17,78 34,58
32,65 27,75 18,02 37,93 32,49 27,64 17,81 37,85 32,91 27,94 18,13   32,75 27,86 18,09 37,93
34,85 28,75 18,33 39,82 34,55 28,7 18,36 39,52 34,95 28,9 18,47 39,89   28,86 18,59 39,87
36,45 30,15 19,96 41,6 36,41 30,02 19,89 41,45 36,69 30,35 20,02 41,71 36,6 30,33 20,05 41,72
38,55 31,65 20,22 ? 38,32 31,55 20,14 ? 38,75 31,77 20,31 ? 38,71 31,84 20,23 ?

 

Вариант 29 Вариант 30 Вариант 31 Вариант 32
XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y XI X2 X3 Y
  12,65 8,84 10,24 5,36 13,1 9,36 10,47 5,36 13,07 9,46 10,7 5,15 14,02 9,53 11,36
7,17 14,29 10,24 13,39 7,64 14,53 10,49 13,52 7,72 14,71 10,89 13,5 8,41 15,23 11,24 14,08
8,83 16,48 11,21 14,19 8,99 16,84 11,37 1188,75 9,3 16,71 11,7 14,41 9,62 16,86 12,21 15,23
11,4 17,01 11,34 15,99 11,76 17,39 11,58 16,48 11,91 17,37 11,58 16,24 12,27 17,39 12,19 17,12
13,39 17,66 13,18 19,74 13,54 17,92 13,43 19,79 13,43 17,93 13,7 20,19 14,32 18,92 13,57 20,18
16,04 19,77 13,27 21,32 16,28 20,17 13,41 21,55 16,68 20,09 13,67 21,8 16,48 20,22 13,76 22,25
18,7 21,59 14,4 23,82 19,07 21,99 14,53 24,03 19,02 21,96 14,5 24,17 19,62 22,6 14,91 23,97
  22,81 16,3 25,98 21,35 23,35 16,53 26,45 21,49 23,11 16,8 26,6 21,48 24,18 17,21 26,59
23,85 24,46 16,42 30,12 24,23 24,79 16,49 30,38 24,06 24,96 16,84 30,67 24,91 24,87 16,73 30,55
25,42 25,06 17,08 29,87 25,77 25,44 17,31 30,2 25,63 25,59 17,35 30,02 26,08 25,73 17,47 30,57
27,74 25,14 16,7 32,17 27,92 25,4 16,84 32,46 27,88 25,38 17,13 32,79 28,59 25,36 17,33 32,76
28,75 27,25 19,09 35,18 29,15 27,58 19,41 35,55 29,03 27,68 19,32 35,58 29,44 27,78 19,82 36,07
30,09 27,51 17,56 34,49 30,37 27,57 17,87 3183,75 30,46 27,69 18,26 34,44 30,53 27,91 18,14 34,62
32,5 27,74 17,88 37,91 32,94 27,92 18,17 37,97 32,76 28,02 18,19 37,96 33,61 28,8 18,7 38,1
34,62 28,69 18,21 39,82   28,97 18,52 40,01 34,83 28,93 18,75 40,02 35,62 29,19 19,12 40,25
36,3 30,1 19,71 41,49 36,51 30,47 20,15 41,95 36,49 30,36 20,34 41,74 37,4 30,84 20,69 42,66
38,46 31,58   ? 38,72 31,9 20,52 ? 39,06 31,98 20,72 ?   32,51 21,19 ?

 

 

 

Пример выполнения задания №3.

 

Исходные данные факторов размещаем в блоке b3:d18 ( табл.3.1), а показатели в столбце e3:e18. Для нахождения корреляционной матрицы нормализуем статистические данные за формулой

, (t=1,n), (j=1,m),

где n - число рассмотренных периодов,

m - число факторов,

- среднее значение фактора Хі,

- среднеквадратичное отклонение фактора Хі.

1.Нормализованные статистические данные рассчитываются по формуле

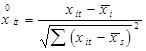
с помощью статистических функций СРЗНАЧ (блок b21:e21), СТАНДОТКЛОН ( блок и27:и29), математической функции КОРЕНЬ и формируются в блоке f13:h17,или с помощью статистической функции НОРМАЛИЗАЦИЯ.

 

2.Элементы корреляционной матрицы, которая находится в блоке a23:c25, можно найти тремя способами:

1. Используя статистическую функцию СУММПРОИЗВ элемент, который находится в i -му строке и j -му столбцы, находим таким чином: СУММПРОИЗВ (столбец нормализованных статистические данные i -го фактора, столбец нормализованных статистические данные j -го фактора).

2. Используя последовательно встроенные функции: ТРАНСП (блок матрицы) и МУМНОЖ (блок данных первой матрицы; блок данных второй матрицы) за формулой

,

(если использовалась статистическая функция НОРМАЛИЗАЦИЯ, то * )

где R - корреляционная матрица;

- матрица нормализованных статистических данных факторов блока f3:h17.

- транспонированная матрица по отношению к матрице .

3. Не нормализуя статистические данные, а используя статистическую функцию КОРРЕЛ (коэффициент корреляции между двумя однородными множествами данных. Предположим, что для факторов Х1, Х2 коэффициент корреляции находится в воротничке b23 за формулой =КОРРЕЛ( b3:b17;c3:c17).

3.Для нахождения рассчитываем определитель матрицы в ячейке 24 используя встроенную математическую функцию МОПРЕД (блок корреляционной матрицы): (= МОПРЕД (a23: c25)). Расчетное значение размещаем в ячейке e25 и находим его по формуле

 

.

 

Логарифм находим используя встроенную математическую функцию LN. Для доверительной вероятности 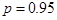и числа степеней свободы 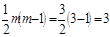, табличное значение .

Поскольку расчетное значение и оно больше критического, то с надежностью можно считать, что существует общая мультиколлинеарность.

4.Используя t-статистику, найдем пары факторов, между которыми существует мультиколлинеарность. Для этого найдем обратную матрицу С = R-1 (блок a27:c29) по отношению к корреляционной матрице R (блок a23:c25)

 

используя встроенную статистическую функцию (блок корреляционной матрицы), то есть в ячейках a27:c29 расположим функцию =МОБР( a23:c25).

5.t-статистику пары факторов рассчитаем за формулой

, где ;

cij, cii, cjj - элементы матрицы C.

Значение 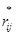и tij находятся в столбцах соответственно e27:29 и g27:29. Для степеней свободы k=n-m-1=15-4=11 и критическое значение 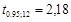. Отсюда значит, что лишь для пары факторов Х1 и Х3 , то есть с надежностью между факторами Х1 и Х3 существует мультиколлинеарность. Выключаем из рассмотрения один из факторов, например Х3.

6.В блоке f23:g24 находим корреляционную матрицу факторов Х1 и Х2. Обратная матрица находится в блоке h23:и24, ее определитель D[X2] вычисляется в ячейке b29. Значение в ячейке b40 меньше критического, это значит, что общая мультиколлинеарность между факторами Х1 и Х2 отсутствует. На отсутствие мультиколлинеарности указывает и t-статистика, значение которой вычисляется в ячейке i25.

7.Допустим, что между показателем Y и факторами Х1, Х2 существует линейная зависимость . Найдем оценки параметров, используя матричные операции. Запишем систему нормальных уравнений в матричной форме

 

.

 

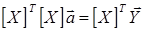Если умножить матричное уравнение слева на матрицу 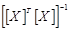, то для оценки параметров вектора получим формулу

 

.

 

Порядок нахождения оценок параметров регрессии:

1. Находим транспонированную матрицу в блоке a31:o33 по отношению к матрице 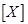в блоке a3:c17, используя в категории "Ссылки и массивы" встроенную функцию ТРАНСП (a2:c17).

2. Находим произведение матриц в блоке a35:c37, используя встроенную математическую функцию МУМНОЖ (блок данных первой матрицы a31:o33; блок данных второй матрицы a3:c17).

3. Обратную матрицу 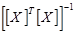находим в блоке d35:f37, используя встроенную математическую функцию МОБР (a35:c37).

4. Произведение матриц 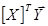находим в блоке h35:h37, встроенную математическую функцию = МУМНОЖ (a31:o33,e3:e17).

5. Оценки вектора находим в блоке g39:g41, встроенную математическую функцию = МУМНОЖ h35:h37)).

 

Порядок нахождения оценок параметров регрессии, используя встроенную статистическую функцию ЛИНЕЙН:

1. Отмечаем блок, где должны находиться расчетные данные: ширина блока равняется числу оцениваемых параметров, а высота равняется пяти строкам.

2. Открываем диалоговое окно Мастер функций, выбираем функцию ЛИНЕЙН в поле категории СТАТИСТИЧЕСКИЕ и нажимаем кнопку Далее> для перехода в следующее окно.

3. В втором диалоговом окне вводим: в первую строку (в первое поле) блок данных показателя, указывая диапазон каморок e3:e17 или имя блока данных; в вторую строку - блок данных факторов a3:a17 или имя этого блока; в третью строку слово ИСТИНА, если а0 не равняется нулю, и слово ЛОЖЬ, если а0 равняется нулю; в четвертую строку вводится слово ИСТИНА, если необходимо найти не только параметры линии регрессии, а и дополнительную регрессионную статистику. Если необходимо найти лишь параметры линии регрессии, то вводим слово ЛОЖЬ и нажимаем слово ГОТОВО для получения расчетных данных.

4. Для того, чтобы в блоке расчетных данных было видно не только значение первой ячейки, нажимаем клавишу F2, а затем Ctrl+Shift+Enter.

Таблица расчетных значений дополнительной регрессионной статистики имеет вид:

 

 

а2 а1 а0
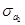
S #Н/Д
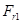
K #Н/Д
#Н/Д

 

 

Описание расчетных данных:

В первой строке находятся оценки параметров множественной линейной регрессии в обратном порядке,т.е. соответственно а0, а1, а2.

В второй строке находятся средние квадратичные отклонения соответствующих оценок параметров .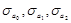

В третьей строке в первой ячейке находится коэффициент детерминации, а в второй - среднее квадратичное отклонение показателя у.

В четвертой строке в первой ячейке находится расчетное значение F-статистики, а в второй - k-число степеней свободы.

В пятой строке в первой ячейке находится сумма квадратов отклонений расчетных значений показателя от его среднего значения, а в второй - остаточная сумма квадратов.

Сравним расчеты, полученные разными методами. Оценки параметров, полученные с использованием матричной алгебры и встроенной статистической функции ЛИНЕЙН, совпадают (блок g39:e41, блок c39:e39). Среднеквадратичные отклонения параметров (блок c40:e40, блок b44:b46) также совпадают. Совпадают сумма квадратов отклонений (каморки k19 d43) и расчетные значения F-статистики для индекса корреляции (каморки c42 и d43).

Проверим адекватность принятой модели экспериментальным данным с помощью критерия Фишера. Дисперсия находится в ячейке f21 ³ вычисляется с использованием встроенной статистические функции СУММПРОИЗВ( h3:h17,h3:h17 )/ 12. В столбце и3:и17 находятся расчетные значения показателя, а в столбце j3:j17 их отклонение от экспериментальных значений.

Расчетное значение критерия равняется 885, а критическое для 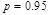, K1=2, K2=12 равняется 3,89. Поскольку F розр> F крит, то с надежностью можно считать, что принятая математическая модель адекватная экспериментальным данным. Расчетное значение F-критерия находится в каморках d45 и c42.

Рассмотрим значимость параметров регрессии. Для этого рассчитаем t-статистику любого из параметров за формулой

 

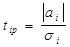, где ,

 

Si - среднеквадратичное отклонение статистических данных от расчетных,

сii - диагональный элемент матрицы С.

Расчетные значения находятся в столбце b47:b49.

Так как t розр> t крит (ячейка b50), то с надежностью можно считать, что влияние факторов Х1, Х2 на показатель Y значительный и их нужно учитывать при расчетах. Точкову оценку значения прогноза для Х1 =9, Х2= 30 находим в воротничке. Доверительный интервал этой точечной оценки находим в столбце и вычисляем по формуле:

,

где .

 

 

Алгоритм расчета доверительного интервала прогноза:

1. Используя встроенную математическую функцию МУМНОЖ (блок вектора a18:c18, блок матрицы [Z] d35:f37), находим произведение (блок h44:j44).

2. Используя встроенную математическую функцию СУММПРОИЗВ (h44:j44, a18:c18), находим в ячейке h45 значение .

3. Используя встроенную математическую функцию КОРЕНЬ, находим в ячейке h46 значение Sур, а затем в ячейке h47 - t*Sур.

4. Доверительные границы прогноза находим в блоке h48:h49.

Частные коэффициенты эластичности для прогноза находим по формулам в ячейках, соответственно b42, b43.

Таблица 3.1 Множественная линейная регрессия

 

  A B C D E F G H I J K L M N O
                               
  X0 X1 X2 X3 Y X1n X2n X3n Yr L L2        
    3.82 10.11 23.20 26.02 -0.46 -0.28 -0.44 27.51 -1.49 2.22 -16.49      
    4.33 12.34 24.49 33.10 -0.38 -0.17 -0.39 32.60 0.50 0.25 -9.41      
    4.82 18.45 26.80 46.15 -0.30 0.13 -0.30 45.40 0.75 0.57 3.64      
    5.23 15.78 28.09 41.15 -0.23 0.00 -0.25 40.58 0.57 0.32 -1.36      
 

⇐ Предыдущая891011121314151617





Date: 2015-10-22; view: 330; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.102 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию