Пространственная корреляция возмущений

(Гетероскедастичность)

Методы случайных выборок, приобретающие все большее значение в эмпирических исследованиях, связаны с обработкой больших объёмов пространственных данных. При работе с набором таких данных могут проявляться пространственные связи в виде пространственных корреляций, возмущений Они нарушают предпосылку классической регрессионной модели и отрицательно сказываются на 1-МНК оценщике. Эти последствия отсутствуют если пространственная корреляция возмущений является равновеликой.

ОПРЕДЕЛЕНИЕ: Возмущение в регрессионном уравнении проявляют равновеликую пространственную корреляцию, если:

1. для t=1,2,…,T-условие гомоскедастичности.

2. где

Выполнение предпосылки с равновеликой пространственной корреляции приводит к обобщённой модели с ковариационной матрицей:

При этом обычные 1-МНК оценки , рассчитанные на основе исходной матрицы данных, идентичны оценкам Эйткена .

ОПРЕДЕЛЕНИЕ: Гетероскедастичность возмущений имеет место, если существует хотя бы один

Пути устранения отрицательных последствий при гетероскедастичности возмущений такие же как и при автокорреляции:

1. Стремится к свободной от гетероскедастичности спецификации модели:

2. Провести оценивание по методу Эйткена.

При диагностике на гетероскедастичность используются различные статистические тесты. Наиболее распространённым и простым является тест Гольдфельда- Квандта.

При тесте Г-Ф нулевая гипотеза имеет вид:

для t=(1,2,…,T)

Альтернативная:

Существует по меньшей мере один

В первом варианте теста Г-Ф на гетероскедастичность возмущений делят все T наблюдений на две группы, так, что в первую входят наблюдений с предположительно меньшей дисперсией, вторую группу образуют наблюдений с предположительно большей дисперсией. Тем самым матрица будет разделена на два блока:

в каждом из которых проводят оценку по 1-МНК. В качестве тест статистики используют величину:

где 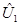представляет собой вектор остатков регрессии в блоке оцененный 1-МНК. Тест статистика имеет распределение с T₂-K и T₁-K степенями свободы.

Нулевая гипотеза отклоняется, если:

Тест Г-Ф может быть применён если и матрицы X₂ обладают полным рангом.

Чувствительность теста Г-Ф может быть повышена, если при разделении на группы исключить m средних наблюдений (второй вариант теста).

При T=30 рекомендуется исключать 8 строк, при T=60-16 строк.

Исходная матрица данных при гетероскедастичность может быть преобразована следующим образом:

При этих вычислениях используется матрица преобразования:

поэтому вспомогательная модель для периода t будет следующая:

Для определения диагональных элементов матрицы применяют два способа:

1. Определение без статистической оценки:

2. Определение по принципу «гетероскедастичность между гомоскедастичными группами».

Оценки 1-МНК преобразованной относительно гетероскедастичности матрицы данных идентичны оценкам Эйткена.

Date: 2015-10-22; view: 331; Нарушение авторских прав