
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. Ряды данных представим в таблице. yt X11 X12 X13
|
|
Ряды данных представим в таблице.
| yt | X11 | X12 | X13 |
Составим модель:

Проведем статистические оценки модели. Для этого:
1. Найдем произведение матриц  .
.
 *
*  =
= 
II. Найдем обратную матрицу 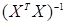 .
.
Для этого:
1. Вычислим определитель:
 2.Найдем алгебраические дополнения для каждого элемента:
2.Найдем алгебраические дополнения для каждого элемента:

 ;
;  ;
; 
 ;
;  ;
; 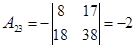
 ;
;  ;
; 
3. Составим союзную матрицу из соответствующих алгебраических дополнений деленных на величину определителя.

4. Транспонируем союзную матрицу (строки запишем столбцами).

В результате получим обратную матрицу 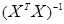 . Для проверки правильности нахождения обратной матрицы
. Для проверки правильности нахождения обратной матрицы 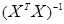 необходимо перемножить исходную
необходимо перемножить исходную  матрицу и обратную
матрицу и обратную 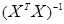 . Если в результате получится единичная матрица, то обратная матрица найдена верно.
. Если в результате получится единичная матрица, то обратная матрица найдена верно.
Вычислим вектор  :
: 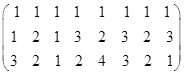 *
*  =
= 
III. Рассчитаем вектор регрессионных коэффициентов, оцененных методом 1-МНК:

Эмпирические регрессионные коэффициенты интерпретируются следующим образом. Если при прочих равных условиях регрессор Х2 возрастает на единицу (уменьшается), то оцененное значение регрессанда также возрастает (уменьшается) на 0,57 (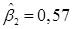 ). Аналогично – если Х3 возрастает (уменьшается) на единицу, то регрессор увеличивается (уменьшается) на 0,09 (
). Аналогично – если Х3 возрастает (уменьшается) на единицу, то регрессор увеличивается (уменьшается) на 0,09 (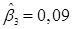 ). Если значения обоих регрессоров равны нулю, то значение регрессанда равно
). Если значения обоих регрессоров равны нулю, то значение регрессанда равно  .
.
Вектор оценок регрессионных коэффициентов 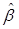 можно найти используя пакет МS Ехсеl. Для этого необходимо:
можно найти используя пакет МS Ехсеl. Для этого необходимо:
1. Найти транспонированную матрицу  по отношению к матрице
по отношению к матрице  , используя в категории «Ссылки и массивы» встроенную функцию ТРАНСП.
, используя в категории «Ссылки и массивы» встроенную функцию ТРАНСП.
2. Найти произведение матриц  , используя встроенную математическую функцию МУМНОЖ.
, используя встроенную математическую функцию МУМНОЖ.
3. Найти обратную матрицу  , используя встроенную математическую функцию МОБР.
, используя встроенную математическую функцию МОБР.
4. Найти произведение матриц  .
.
5. Найти оценки вектора, перемножив матрицы  и
и  .
.
А также с использованием встроенной статистической функции ЛИНЕЙН.
Порядок нахождения оценок при этом следующий:
1. Отметить блок размером Р на 5 в котором будут находиться расчетные данные, где Р-число оцениваемых параметров.
2. Открыть диалоговое окно Мастер функций, выбираем функцию ЛИНЕЙН в поле категории СТАТИСТИЧЕСКИЕ и нажимаем кнопку Далее для перехода в следующее окно.
3. Во втором диалоговом окне вводим: в первую строку данные показателя, указав диапазон ячеек или имя блока данных: во вторую строку - блок данных факторов или имя этого блока; в третью - слово истина (или число 1), если есть свободный член в уравнении регрессии и слово ложъ (или 0). если его нет: в четвертую - слово истина (1). если необходимо найти дополнительную регрессионную статистику или ложь (0) если необходимо найти только парасертры уравнения и нажимаем слово Готово для получения расчетных параметров.
4. Для того, чтобы в блоке расчетных данных получить все расчетные данные, нажимаем клавишу F2, а затем Сtг1 + Shift + Еntег. При этом:
В первой строке будут находиться (справа налево) оценки параметров линейной регрессии.
Во второй строке (справа налево) находятся средние квадратичные отклонения оценок параметров.
В третьей строке в первой ячейке находится коэффициент детерминации,во второй ячейке - среднее квадратичное отклонение показателя у.
В четвертой строке в первой ячейке находится расчетное значение F -статистики, а во второй ячейке – df - число степеней свободы.
В пятой строке в первой ячейке находится сумма квадратов отклонений расчетных значений показателя у от его среднего значения, а во второй ячейке остаточная сумма квадратов.
Результат работы функции ЛИНЕЙН:
| 0,085616 | 0,568493 | 1,849315 |
| 0,396785 | 0,492151 | 1,454415 |
| 0,214155 | 1,08571 | #Н/Д |
| 0,68129 | #Н/Д | |
| 1,606164 | 5,893836 | #Н/Д |
IV. Рассчитаем вектор регрессанда

Ŷ(линейн)
| 2,69 |
| 3,17 |
| 2,51 |
| 3,74 |
| 3,35 |
| 3,83 |
| 3,17 |
| 3,65 |
V. Вектор ошибок (возмущений) имеет вид:

Сумма ошибок равна нулю, следовательно, расчет выполнен верно.
VI. 1-МНК оценщик дисперсии 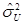 равен:
равен:
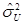 = 5,8976/5 = 1,17952
= 5,8976/5 = 1,17952
VII. Оцененная ковариационная матрица 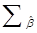 имеет вид:
имеет вид:
| 2,117534 | -0,53342 | -0,37178 |
| -0,53342 | 0,242466 | 0,008082 |
| -0,37178 | 0,008082 | 0,157603 |
Элементы корреляционной матрицы можно также найти следующим образом:
1. Используя статистическую функцию СУММПРОИЗВ (столбец нормализованных данных i-го фактора; столбец нормализованных данных j-го фактора). Найдем элементы в i- той строке j-ом столбце корреляционной матрицы.
2. Используя последовательно встроенные функции ТРАНСП (блок матрицы) и МУМНОЖ (блок данных первой матрицы; блок данных второй матрицы) найдем корреляционную матрицу:

где 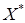 - матрица нормализованных данных,
- матрица нормализованных данных, 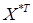 - транспонированная матрица.
- транспонированная матрица.
3. Используя статистическую функцию КОРРЕЛ (блок данных i- го фактора: блок данных j-го фактора) - определяющую коэффициент корреляции между двумя однородными множествами данных, также можно найти все элементы корреляционной матрицы.
VIII. Вычислим оцененную дисперсию ошибки прогноза:
σе2 =ХtТ *∑β* Хt = 0,339452
Тогда соответствующая оцененная стандартная ошибка прогноза:
σе =  =
=  = 0,582625
= 0,582625
IX. Вычислим дисперсию ошибки 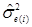
σе(I)2 = σu2 + σе2 = 1,519452
и как следствие, стандартную ошибку 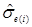 :
:
σе(I) = 1, 232661
X. Найдем 99% прогнозный интервал математического ожидания регрессанда. Для этого рассчитаем точечный прогноз регрессанда  :
:

Тогда прогнозный интервал математического ожидания при степени свободы  :
:
Нижняя граница:
ŷt – t(α, FG)*σе = 3,74 – 0,582625*4,032 =3,74 – 2,349144 = 1,390856 = 1,4
Верхняя граница:
ŷt + t(α, FG)*σе = 3,74 +0,582625*4,032 =3,74 + 2,349144 = 6,089144 = 6,1
XI. Прогнозный интервал для индивидуального значения регрессанда.
Нижняя граница:
ŷt – t(α, FG)*σе(I) = 3,74 – 1,232661*4,032 = 3,74 – 4,9701 = - 1,2301
Верхняя граница:
ŷt + t(α, FG)*σе(i ) = 3,74 + 1,232661*4,032 = 3,74 + 4,9701 = 8,7101
XII. Вычислим коэффициент детерминации  :
:
R2 = 0,2142.
Таким образом, регрессионной функцией будет объяснено 21,42% суммы квадратов отклонений выборки регрессанда от средней или 21,42% вариации у объясняется вариацией факторов х.
XIII. Проверим гипотезу «второй регрессор в генеральной совокупности не оказывает никакого влияния».
Шаг 1. 

Шаг 2. Пусть  .
.
Шаг 3. Найдем по таблице 
Шаг 4. Вычислим

Шаг 5.  может быть отвергнута, если
может быть отвергнута, если 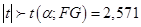
Шаг 6. Так как нулевая гипотеза не может быть отвергнута, то второй регрессор не оказывает влияния на регрессанд.
XIV. Проведем d-тест на автокорреляцию.
Шаг 1. 
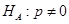
Шаг 2.  по условию.
по условию.
Шаг 3. Найдем табличные значения показателя d для  К= 3, Т= 8
К= 3, Т= 8

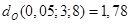
Шаг 4. Вычислим:
d = 
Шаг 5. Так как 0,56 < d > 1,78, то это значит, что d статистика находится в области неопределенных решений.
Шаг 6. В силу принятых условий,будем считать,что гипотеза  может быть отклонена, т.е. автокорреляция есть.
может быть отклонена, т.е. автокорреляция есть.
Date: 2015-10-22; view: 490; Нарушение авторских прав