Основные правила вычисление производной

1.) Постоянный сомножитель можновыносить за знак производной и дифференциала:

и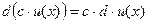

2.) Если ф-ции u и v дифференцируемы в (.) х₀, то их алгебраическая сумма дифференцируема в (.) х₀, причём её производная , а её дифференциал .

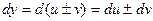3.) Если ф-ции u и v дифференцируемы в (.) х₀, то их произведение дифференцируемо в (.) х₀, причём производная произведения находится по формуле: , а дифференциал .

Док-во:

Дадим х₀ приращение , тогда обе ф-ции u и v получат приращение , а ф-ция получит приращение =

Разделим полученное равенство на : .

Перейдём к пределу при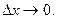

, т.к. правая часть, то :

.

Найдём дифференциал: ч.т.д.

4.) Если ф-ции u и v дифференцируемы в (.) х₀, то их частное дифференцируемо в (.) х₀, причём производная частного находится по формуле: , а дифференциал

Ф-ция f ставит в соответствие числу х число у, а ф-ция φ – числу у число z. Говорят, что ф-ция h есть сложная ф-ция, составленная из ф-ций φ и f, и пишут: h(х)=φ(f(x)).

Пусть дана ф-ция у=φ(t), где t=f(x). Если ф-ция t=f(x) дифференцируема в (.) х₀, а ф-ция у=φ(t) - дифференцируема в (.) t₀=f(х₀), то сложная ф-ция у=φ(f(x)) дифференцируема в (.) х₀, причём её производная , t- промежуточная переменная, х- независимая переменная.

Пр: y=cost, где t=x²-3x

Неявной ф-цией у от х наз. ф-ция, представленная уравнением: F(x,y)=0.

Т: Пусть F(x,y) и обе её частные производные и - непрерывные ф-ции, причём ≠0, тогда ф-ция имеет производную:

Задание ф-ции системой: наз. параметрическим заданием ф-ции.

Пусть ф-ция задана параметрически, тогда выполняются 2 условия:

1] х=φ(t)- непрерывна на [a,b] дифференцируема внутри него;

2] у=ψ(t)- непрерывна на [a,b] дифференцируема внутри него, тогда .

МЕТОДИКА 7. Тема: «Правила вычисления производных»

Данная тема изучается в 10 классе (по учебнику «Алгебра и начала анализа 10-11 кл.» под ред. Алимова Ш.А.) и в 11 классе (по учебнику «Алгебра и начала анализа 10-11 кл.» под ред. Колмогорова А.Н.). На изучение данной темы отводится 2-3 часа.

Ранее изученный материал, необходимый для изучения данной темы: приращение функции, понятие производной. Применение: исследование функций с помощью производной для построения графиков, производная сложной функции, в физике и т.д.

Материал темы. Правила дифференцирования:

1. Производная суммы (разности) равна сумме (разности) производных (f(x)±g(x))'=f'(x)±g'(x)

2. Постоянный множитель можно выносить за знак производной: (C·f(x))'=C·f'(x)

3. Производная произведения: (f(x)·g(x))'=f'(x)·g(x)+f(x)·g'(x)

4. Производная частного:

В учебниках Башмакова и Колмогорова все эти формулы выводятся, каждый шаг объясняется. Учебник Алимова содержит доказательства только двух первых формул, но к каждой формуле есть по 1-2 примера.

В учебнике Колмогорова рассматривается формула производной сложной функции (гл 2, §16):

f(g(x))' = f '(g(x))·g'(x)

Сначала автор дает определение сложной функции, затем выводит формулу и приводит несколько примеров нахождения производной сложных функций. Алимов решил упростить данный раздел, заменив формулу сложной функции на ее частный случай – линейную замену аргумента:

(f(kx + b))' = kf '(kx + b)

Эта формула гораздо менее емкая, зато ее доказательство короче и менее абстрактно. Башмаков же включил в учебник обе формулы.

Цели изучения:

Обучающие: научить уметь обосновывать и применять правила вычисления производных.

Развивающие: развивать самостоятельность учащихся, способность к самоорганизации, готовность к сотрудничеству.

Воспитательные: воспитывать интерес к предмету, культуру общения.

Виды самостоятельных работ с точки зрения организации процесса обучения:

1. фронтальная – учащиеся выполняют одно и то же задание;

2. групповая – для выполнения учебных заданий учащиеся разбиваются на группы (3-6 человек);

3. парная – 2 человека;

4. индивидуальная – каждый ученик выполняет отдельное задание.

Дидактические материалы

Вариант 1

1. Найдите производную функции:

а) f(x)=2x⁷+ 4 ; б) f(x)= .

2. Вычислите производную функции f(x)=2x²+x³ в точках 2; 4; х; х-3.

3. Решите неравенство f'(x)≤0, если f(x)=4x+2x².

4. Найдите производную функции f(x)=50x⁵+5x⁵⁰ в точках х и -1.

5. Решите уравнение f'(x)=0 и неравенства f'(x)>0 и f'(x)<0 для функции:

а) f(x)=x²+3x-3; б) f(x)= .

Вариант 2

1. Найдите производную функции:

а) f(x)=x⁵-2 ; б) f(x)= .

2. Вычислите производную функции f(x)=3x+4x³ в точках 1; 1,5; х; х+2.

3. Решите неравенство f'(x)>0, если f(x)=6x-3x².

4. Найдите производную функции f(x)=100x¹⁰-10x¹⁰⁰ в точках х и 1.

5. Решите уравнение f'(x)=0 и неравенства f'(x)>0 и f'(x)<0 для функции:

а) f(x)=x²-3x+1; б) f(x)= .

Тема урока «Правила вычисления производных»

Цели урока:

Обучающие: формировать умение применять правила вычисления производных при решении задач.

Развивающие: развивать самостоятельность учащихся, способность к самоорганизации, готовность к сотрудничеству.

Воспитательные: содействовать развитию у учащихся чувства ответственности за личную и коллективную деятельность, содействовать учащимся в осознании ценности совместной деятельности.

Тип урока: урок закрепления знаний.

Работа в группах.

Все учащиеся класса разбиваются на 3 группы по своим учебным способностям. Группа № 1 получает карточки с I вариантом; № 2 – со II вариантом; № 3 – с III вариантом.

В классе стоят столы. За стол № 1 садятся ученики, у которых будут все 3 варианта. И так за каждый собирается группа из 3 человек с разными вариантами с I по III. Каждый ученик в течение 15 минут работает самостоятельно с карточкой своего варианта. После выполнения работы ученики перемещаются так, чтобы за столом №1 собрались ученики, у которых был I вариант, за столом № 2 – II вариант и т.д.

На каждый стол выдается конверт, в котором находятся ответы к данному варианту и контрольный лист с критериями оценок. Учащимся отводится время (5-7 минут) для проверки своего решения, разбора в группе своих ошибок и их исправления, выставления оценок.

Примеры карточек по вариантам

Вариант №1	1. Найдите f'(x), если f(x)=(1+2x)(2x-1).	1. Вычислите производную функции f(x)=2x2+x3 в точках 2; 4; х; х-3.	1. Решите неравенство f'(x)≤0, если f(x)=4x+2x2.
Вариант №2	2. Найдите производную функции: а) f(x)=2x7+ 4 ; б) f(x)= .	2. Найдите g'(-1), если g(x)=(x-1) .	2. Решите уравнение f'(x)=0, если f(x)=2x3-3x2+1.
Вариант №3	3. Найдите производную функции: а) f(x) = x7+2x5- 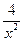-1; б) f(x)= .	3. Найдите производную функции f(x) = в точках x и t4.	3. Решите уравнение f'(x)=0 и неравенства f'(x)>0 и f'(x)<0, если: а) f(x)=3x3-x; б) f(x)= .

Билет № 8. «Ряды».

Возьмём бесконечную числовую послед-ть х₁, х₂, …, x_n,…. Члены данной послед-ти соединим знаком «+», тогда получим выражение (*) х₁+х₂+ …+x_n+…. = , которое наз. числовым рядом.

Составим послед-ть частичных сумм ряда:

Суммой ряда наз. конечный предел послед-тей частичных сумм: , тогда равенство (*) наз. сходящимся, в противном случаи ряд (*) расходящийся (если предел не или равен )

(Необходимый признак сходимости) Если ряд сходится, то его общий член стремится к нулю, т.е. - сх-ся или .

Док-во:

Т.к. ряд сх-ся, то конечный предел .

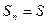
ч.т.д.

Следствие: если общий член не стремится к нулю, то ряд - расходится.

Признаки сравнения числовых рядов (достаточные признаки):

Т1: Пусть даны два ряда: (1) 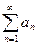и (2) , тогда из сходимости ряда (2) сходимость ряда (1) и из расходимости ряда (1) расходимость ряда (2).

Т2: Пусть даны два ряда: (1) 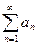и (2) 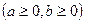, тогда если 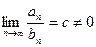, то оба ряда ведут себя одинаково: сходятся или расходятся.

Т3: (признак Д’Аламбера) Пусть дан ряд 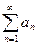, если предел отношения последнего члена к предыдущему есть число q, то при q<1 – ряд сходится, q>1 – расходится, q=1 – ряд ответа не даёт.

Док-во: Н/р,рассмотрим при q>1 начиная с некоторого номера n₀ все члены послед-ти . Члены ряда возрастают, ряд расходится.

Т4: (радикальный признак Коши) Пусть дан ряд 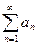, если предел , то c<1 – ряд сходится, c>1- расходится, c=1 – признак ответа не имеет.

Т5: (интегральный признак Коши) Пусть дан ряд 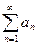, и ф-ция f(x) - такова, что для неё выполняются следующие условия: 1) f(x)>0; 2) f(x) – строго убывает для ; 3) f(x) – непрерывна для ; 4) f(n)=a_n, тогда поведение ряда совпадает с поведением несобственного интеграла .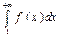

Пусть дан знакочередующийся ряд (1) , т.е. такой, в котором два соседних члена имеют противоположные знаки: .

Т Лейбница: Пусть в ряде (1) члены по модулю убывают и предел общего члена равен нулю , то ряд (1) будет сходится (S>0,S<a₁). (эту теор. м/о использовать для приближённых вычислений)

Док-во: Рассмотрим суммы ряда (1) с чётными индексами:

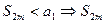- ограничена сверху.

Докажем, что послед-ть частичных сумм - монотонно возрастает:

монотонно возрастает, а на основании теор. (если послед-ть монотонно возрастает и ограничена сверху, то она имеет верхний предел): .

Докажем, что послед-ть частичных сумм с нечётными индексами имеет тот же самый предел:

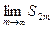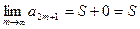
+ ряд (1) сходится.

Пр: , т.е. - гармонический ряд. сходимость по Лейб

Ряд (2) наз. знакопеременным, если среди его членов имеются «+» и «-», а знакочередующийся ряд явл-ся для него частным случаем.

Т: Если знакопеременный ряд (2) таков, что ряд (3) составлен из модулей его членов – сходится, то и ряд (2) тоже сходится.

Знакопеременный ряд (2) наз. абсолютно сходящимся, если он сходится, и ряд по модулю (3) тоже сходится, и обратно, если сходится ряд (3), то ряд (2) наз. абсолютно сходящимся.

(п3) сх-ся, составим ряд из модулей членов этого ряда - расх-ся дан. ряд условно сх-ся.

МЕТОДИКА 8. 1) Логико-математический анализ темы

Логико-математический анализ темы: Геометрическая прогрессия (по учебнику Алгебра 9 класс под ред. Ш.А Алимова, Ю.М.Колягина)

Date: 2015-10-18; view: 1666; Нарушение авторских прав