Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Фрагмент урока изучения новой темы: «Логарифмическая функция»
|
|
Цели урока:
Образовательные: обеспечить в ходе урока усвоения понятия логарифмическая функция, формировать умения определять свойства логарифмических функций, формировать умение изображать графики логарифмической функции.
Развивающие: способствовать развитию мышления, восприятия, памяти, воображению, внимания.
Воспитательные: воспитывать устойчивый интерес к математике, воспитывать отдельные качества личности: аккуратность, настойчивость, трудолюбие.
Тип урока: изучение нового материала
Структура урока:
1. организационный момент
2. постановка целей урока
3. проверка домашнего задания
4. подготовка к изучению нового материала
5. изучение нового материала
6. первичное закрепление и осмысление нового материала
7. постановка домашнего задания
8. подведение итогов урока.
| Действия учителя | Действия учеников | |||||||||||||
ответьте на вопрос
1. что называется функцией?
2. какие функции вы узнали в этом году?
3. какие свойства функций вы знаете?
4. что называется графиком функции?
Сегодня мы изучим новую функцию логарифмическую. Когда мы изучали показательную функцию, мы оформляли ее свойства в таблицу. Сейчас я предлагаю открыть вам страницу 98 в ваших учебниках прочитать параграф 18 и записать в тетрадях опорный конспект по плану предложенному на доске. Опорный конспект вы будите оформлять так же, как оформляли при изучении показательной функции.
План опорного конспекта.
1. определение логарифмической функции
2. свойства логарифмической функции оформите в таблицу.
А теперь к доске я приглашаю одного человека который оформит правильно конспект на доске.
|
1. Числовой функцией с областью определении D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х.
2. степенная, показательная.
3. Область определения, область значений, непрерывность, возрастание, убывание функции.
4. Графиком функции f называют множество всех точек (х; у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.
Ответы: Функцию, заданную формулой у=logах, где а>0, а≠0 называют логарифмической функцией с основанием а.
|
Билет № 6. «Тригонометрические функции».
Синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями.
Опр. Ф-ции, заданные формулами y=sinx и y=cos x, называются соответственно синусом и косинусом.
Св-ва синуса и косинуса:
1) D(y)=(-∞;+∞).
2) E(y)=[-1;1].
3) y=cos x – чётная ф-ция, т.е. cos (-x)= cos x
y=sin x – нечётная ф-ция, т.е. sin (-x)= -sin x
4) y=sin x и y=cos x явл-ся периодическими и наименьший положительный период равен 
.
cos (x+ 
)= cos x, sin (x+ )= sin x (n 
z).
Док-во:
Пусть Т – произвольный положительный период косинуса, то 
при любом α.
Полагая, что 
, находим 
Наименьшее положительное число Т, для которого cos x=1, есть .
Пусть Т – произвольный положительный период синуса, то 
Полагая, что 
, находим 
Но sinx=1 только при 
. Поэтому Т=2 
. Наименьшее положительное число 2 есть .
5) y=sin x возрастает на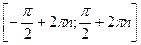 
и убывает на 
y=cos x возрастает на и убывает на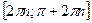 
6) графики:
y=sinxy=cos x
Опр. Ф-ции, заданные формулами y=tgx и y=ctg x, называются соответственно тангенсом и котангенсом.
Св-ва тангенса и котангенса:
1.) D(tg) все числа х для которых cos x≠0, т.е. х≠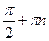 
(n z).
D(сtg) все числа х для которых sin x≠0, т.е. х≠ (n z).
2.) E(y) – вся числовая прямая.
3.) y=tg x и y=сtg x – нечётные ф-ции, т.е. tg (-x)= - tgх; сtg (-x)= - сtgх;
4.) y=tg x и y=сtg x явл-ся периодическими и наименьший положительный период равен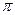 
.
tg (x+ )= tg x, сtg (x+ )= сtg x (n z).
Док-во:
Пусть Т – произвольный положительный период тангенса, то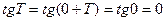 
. Т.к. на интервале 
тангенс нулей не имеет, 
. А 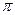- это период ф-ции тангенс и значит 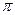- это наименьший положительный период тангенса. Для y=сtg x док-во аналогичное.
5.) y=tg x возрастает на 
, а y=сtg x убывает на 
.
6.) графики:
y=tg x y=сtg x
Ф-ции синус и косинус непрерывны на всей обл. определения, а значит дифференцируемы. Рассмотрим разложения функций в степенной ряд.
f(x)=sin x
Рассмотрим ряд Тейлора: 
, это частный случай, когда х0=0 (ряд Маклорена).
→ 
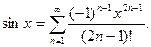
y=cos x разлаживается аналогично: 
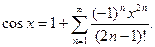
МЕТОДИКА 6. Фрагмент урока изучения нового материала
Цели урока:
Обучающая – ввести определения тригонометрических функций и научить строить их графики;
Развивающая – развитие познавательных процессов, общеучебных умений;
Воспитательная – воспитание интереса к математике, аккуратность.
Ход урока
| Деятельность учителя | Деятельность учащихся |
| 1.«Давайте вспомним: Что такое функции? (из курса алгебры 9 кл) Будет ли функцией y=sinx и y=cosx? 2. Тема урока: Тригонометрические функции y=sinx, y=cosx. Кратко рассказывает о работе на данном уроке. 3. Объяснение нового материала, а именно: - определение единичной окружности; - определение функций синус и косинус; - область определения функций y=sinx, y=cosx; - область значений функций синус и косинус; - чётность и нечётность функций; - периодические функции; - промежутки, на которых функция принимает положительные значения; - промежутки, на которых функция принимает отрицательные значения; - наибольшее значение, равное 1; - наименьшее значение равное -1. 4. Строим график функции синус на отрезке [0;2п]. График синуса называется синусоидой. Строим график функции косинус, используя cosx = sin(x+п/2). (параллельный перенос графика синус на расстояние п/2 в отрицательном направлении оси ОХ, рис.9). 5. Построить график функции: 1) y=3sinx 2) y=(1/2) sinx | Слушают, отвечают на вопросы, работают с учителем. Слушают учителя. Слушают, делают записи в тетрадях, работают с учителем по учебнику. Строят графики в тетрадях с помощью линейки и карандаша. Занимаются решением и построением графика. |
Средства наглядности: таблицы, мультимедийный проектор, компьютер.
Создание проблемной ситуации (например: Как построить функцию?).
Билет № 7. «Производная».
Рассмотрим на мн-ве Х ф-цию у=f(x), выберем внутреннею (.)х0 этого мн-ва (т.е. если 
такая окрестность (.)х0, которая целиком мн-ву Х) и найдём 
. Дадим х0 приращение 
, получим новое значение аргумента 
, вычислим 
. Составим разность, которую назовём приращением ф-ции и обозначим 
: 
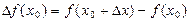.Составим отношение приращения ф-ции к приращению аргумента и вычислим предел отношения 
при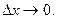 
Производной ф-цииу=f(x)в (.) х0 наз. конечный предел отношения приращения ф-ции к вызвавшему его приращению аргумента, при 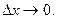Т.е. 
.
Если приращение ф-ции в (.)х0 м/б представлено в виде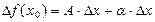 
, то ф-цию у=f(x) наз. дифференцируемойв (.) х0, где 
- это число не зависящее от 
(производная),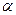 
- это бесконечно малая величина 
при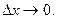
Выражение 
наз. дифференциалом ф-цииу=f(x)в (.) х0. 
или 
, где - приращение независимой переменной.
Date: 2015-10-18; view: 687; Нарушение авторских прав