Тема 7. Изгиб прямых брусьев

Эта тема является самой большой и самой сложной темой курса сопротивления материалов; ее сле­дует изучать посте­пенно, обращая особое внимание на решение задач. Сначала надо усвоить весьма важные понятия изгибающего момента М и поперечной силы О и научиться свободно строить эпюры Ми б.

Необходимо помнить, что поперечная сила в данном сечении равна алгебраической сумме проек­ций сил, рас­положенных только по одну сторону от рассматриваемого сечения, на перпендикуляр к оси балки, а изгибающий момент в данном сечении равен алгебраической сумме моментов сил, располо­женных только с одной стороны, относительно центральной оси поперечного сечения. В связи с этим рекомендуется - при вычислениях, напри­мер, изгибающего момента в сечении балки как момента левых сил - закрывать чем-либо (рукой, книгой, лис­том бумаги) часть балки, расположенную правее рассматриваемого сечения, чтобы открытыми оставались только одни левые силы. Следует при этом иметь в виду, что можно рассматривать как одни левые, так и одни правые силы, в зависимости от то­го, с какой стороны проще получить выражения Q, и M. Весьма важное значение имеет теорема Журавского, устанавливающая зависимость между Q и М, с помощью которой можно проверять построение эпюр.

Необходимо обратить внимание на неравномерность распределения нормальных напряжений по высоте балки и на то, что прочность балки зависит от момента сопротивления W. Надо ясно представ­лять, каким путем можно увеличить момент сопротивления без увеличения расхода материала.

Рекомендуется сравнить между собой эпюры s и t, построенные для балки прямоугольного попе­речного сечения. Наибольшее и наименьшее нормальные напряжения (главные напряжения) на­ходят по формуле: .

Необходимо разобрать графическое построение, при помощи которого можно получить эту форму­лу.

Надо внимательно изучить вопрос о центре изгиба. В работе проф. В.3. Власова «Тонкостенные упругие стержни» этот вопрос рассмотрен более подробно и дана законченная теория изгиба и круче­ния тонкостенного профиля произвольного очертания. После этого следует перейти к изучению дефо­рмаций при изгибе. Правая часть дифференциального уравнения изогнутой оси балки содержит выра­жение изгибающего момента в произвольном сечении данного участка, а не в том сече­нии, для которо­го находят перемещения (углы поворота и прогибы), М(х) - величина переменная; только в случае чис­того изгиба М(х)=const. Надо хорошо понять геометрический смысл постоянных интегрирования С и D, разделив их на ЕI, по­лучим соответственно угол поворота и прогиб в начале координат.

При наличии нескольких участков, когда изгибающий момент от сосредоточенных сил или момен­тов выражается раз­личными уравнениями, необходимо интегрировать без раскрытия скобок, так как только при соблюдении этого требования произвольные постоянные будут соответственно равны меж­ду собой (С₁=С₂=...=С И D₁=D₂=...=D).

Распределенную нагрузку можно преобразовать и получить соответственно равные произвольные постоянные также и в том случае, когда она на каком-либо участке балки обрывается.

В результате можно получить общие уравнения углов поворота и прогибов, которыми и следует преимущественно поль­зоваться при решении задач аналитическим методом. Обычно начало координат помещают на левом конце балки и общие уравнения углов поворота и прогибов пишут так:

(2)

Здесь a_m, a_p, a_q - соответственно абсциссы точек приложения сосредоточенной пары M, силы P, начала равномерно рас­пределенной нагрузки с интенсивностью q, знаки сумм распространяются на все нагрузки, расположенные слева от того се­чения балки, для которого находят прогиб и угол поворота. Величины y₀, q₀, М₀, Q ₀, обозначающие соответственно прогиб, угол поворота, изгибающий момент и поперечную силу в начале координат, называются начальными параметрами. В связи с этим метод оп­ределения деформаций балки при по­мощи написанных выше уравнений называют часто методом на­чальных параметров. Два начальных параметра из четырех известны при любом способе опирания ле­вого конца балки. Действительно, для защемленного конца у₀=0 и q₀=0; для шар­нирно опертого конца у₀=0 и М ₀ = 0 (если на левом конце приложен момент М, то М ₀ =М); для свободного конца Q₀=0 (если на левом конце приложена сила P, то Q₀=Р) и М₀=0 (или М₀=M).

Для статически определимой балки начальные параметры Q₀ и М ₀ легко найти при помощи уравне­ний статики; таким образом, в случае защемленного левого конца известны все четыре начальных па­раметра, в случае шарнирно опертого конца неизвестна только величина q₀, в случае свободного конца неизвестны величины y₀ и q₀.

Неизвестные начальные параметры находят из условий на правом конце балки. Например, для бал­ки, свободно лежащей на двух опорах, при определении q₀ надо использовать то условие, что прогиб на правой опоре равен нулю.

Неразрезные балки рассчитывают при помощи уравнений трех моментов. При наличии нагрузки на консоли неразрезной балки в левую часть уравнения трех моментов надо подставить значение изгибаю­щего момента на крайней опоре, учитывая его знак: момент считается положительным, если он изгиба­ет консоль выпуклостью вниз. В случае защемления на крайней опоре надо присоединить к балке до­полнительный пролет, написать уравнение трех моментов в обычной форме и затем про­извести упро­щения, т. е. приравнять нулю длину дополнительного пролета и момент на крайней его опоре. Этот прием по­зволяет рассчитывать при помощи уравнения трех моментов и однопролетные балки с защем­ленными концами.

Однопролетные статически неопределимые балки легко можно рассчитать и при помощи метода начальных параметров. Для примера рассмотрим балку с защемленными концами, нагруженную рав­номерно распределенной нагрузкой на всей длине. В данном случае y₀=0 и q₀=0; в виду симметрии мо­жно написать, что Q₀=ql/2, уравнения (1) и (2) примут такой вид:

Неизвестный начальный параметр М ₀ найдем из условия на правой опоре: при x = l q=0 (можно ис­пользовать также ус­ловие: при х=l у=0).

Отсюда находим: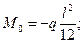

Таким образом, мы не только нашли опорный момент, но и одновременно получили уравнения уг­лов поворота и проги­бов. При решении не возникло никаких дополнительных затруднений, несмотря на то, что данная задача статически неопре­делима.