Тема 5. Геометрические характеристики плоских сечений

Литература: [1, гл. 5]; [2, гл. 3]; [3, гл. 5, задачи 1, 4, 5, 8, 9,11,13,20,25].

В теории изгиба важную роль играют моменты инерции, поэтому следует рассмотреть этот вопрос предварительно в виде самостоятельной темы. Перед изучением этой темы полезно по учебнику теоре­тической механики повторить материал о статическом моменте и о нахождении центров тяжести плос­ких фигур. При вычислении моментов инерции надо помнить, что они представляют собой интегралы или типа 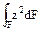(осевой, или экваториальный, момент инерции относительно оси у) или типа (центробежный момент инерции относительно осейz и y).

Необходимо запомнить, что теорема о переносе осей (I_y1 = I_y + a²F) справедлива только в том случае, если ось y проходит че­рез центр тяжести фигуры. Если, например, известен момент инерции треуголь­ника относительно оси, проходящей через ос­нование, то нельзя при помощи теоремы о переносе осей сразу найти момент инерции треугольника относительно оси, про­ходящей через вершину параллельно основанию; сначала необходимо при помощи этой теоремы найти момент инерции от­носительно цент­ральной оси, а затем определить момент инерции относительно оси, проходящей через вершину. Фор­мула переноса осей наглядно показывает, что наименьшим из моментов инерции относительно нес­кольких параллельных осей яв­ляется момент инерции относительно той оси, которая проходит через центр тяжести.

Наименьшим из моментов инерции относительно центральных осей, наклоненных под разными уг­лами, является момент инерции относительно одной из главных центральных осей. Относительно дру­гой главной оси, перпендикулярной к первой, момент инерции имеет, наоборот, наибольшее значение. Центробежный момент инерции относительно главных осей равен нулю", при этом совсем не обяза­тельно, чтобы главные оси проходили через центр тяжести, так как через любую точку, ле­жащую в плоскости фигуры, можно провести такие две взаимно перпендикулярные оси, относительно которых центробеж­ный момент инерции будет равен нулю. В теории изгиба весьма важную роль играют глав­ные центральные оси, положение которых для несимметричных сечений определяют так:

1) сначала проводят случайные оси, вычисляют статические моменты сечения относительно этих осей (разделив предва­рительно сложную фигуру на ряд простых фигур) и находят положение центра тяжести сечения;

2) проводят через центр тяжести всего сечения оси, параллельные первоначально выбранным слу­чайным осям, и находят при помощи теоремы о переносе осей центробежный и осевые моменты инерции сечения относительно этих новых осей;

3) находят положение главных центральных осей и и n по формуле: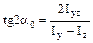

4) находят главные центральные моменты инерции.

Для проверки правильности вычислении I_u и I_n можно использовать равенства: I_u+I_n=I_y+I_z и I_un=0

Следует иметь в виду, что при помощи этих равенств можно проверить вычисления только по п.п. 3 и 4; соблюдение этих равенств не гарантирует правильности вычислений, сделанных в п.п. 1 и 2.

Если сечение состоит из ряда прокатных профилей, то необходимо при вычислениях пользоваться данными таблиц сор­тамента. При определении центробежного момента инерции уголка (равнобокого или неравнобокого) не следует делить площадь этого уголка на два прямоугольника; сначала можно найти центробежный момент инерции всего уголка относи­тельно осей, проходящих через центр тяжес­ти параллельно полкам, при помощи формулы, в которой использованы обозна­чения таблиц сортамен­та:

где I_x0 и I_уо - главные центральные моменты инерции, значения которых даны в таблицах сорта­мента; после этого надо применить формулу переноса осей и найти центробежный момент инерции уголка относительно центральных осей всего сечения.

При пользовании формулой поворота осей надо обязательно обратить внимание на знак угла a: ес­ли для совмещения оси Х_о с осью Х надо повернуть ось Х₀ по часовой стрелке, то угол a следует счи­тать отрицательным.

Вопросы для самопроверки. 1. По каким формулам находят координаты центра тяжести плоской фигуры? 2. Чему равна сумма осевых моментов инерции относительно двух взаимно перпендикуляр­ных осей? 3. Какие оси называются главными? 4. Для каких фигур можно без вычислений установить положение главных центральных осей? 5. Относительно каких цен­тральных осей осевые моменты ине­рции имеют наибольшее и наименьшее значения? 6. Какой из двух моментов инерции треугольника больше: относительно оси, проходящий через основание или относительно оси, проходящей через ве­ршину параллельно основанию? 7. Какой из двух моментов инерции квадратного сечения больше: от­носительно центральной оси, проходящей параллельно сторонам, или относительно оси, проходящей через диагональ? 8. Какой из двух главных цен­тральных моментов инерции полукруглого сечения больше: относительно оси, параллельной диаметру, ограничивающему сечение, или относительно пер­пендикулярной оси?

Date: 2015-10-21; view: 721; Нарушение авторских прав