Упражнения. 1. Доказать, что для матриц выполняются свойства

1. Доказать, что для матриц выполняются свойства

(АВ)С= А(ВС), (А+В)С= АС + ВС, С(А+В)= СА + СВ, АЕ= А, ЕА = А, где Е – единичная матрица (см.5.3). Причем если определена левая часть равенства, то определена правая часть и наоборот.

2. Доказать, что умножение матриц некоммутативно, то есть привести пример матриц А и В таких, что АВ ¹ ВА.

Определение. Матрица В называется левой обратной для матрицы А, если ВА = Е. Матрица С называется правой обратной для матрицы А, если АС = Е.

Утверждение. Если для матрицы А существуют левая

обратная матрица В и правая обратная матрица С, то В = С.

Доказательство. Рассмотрим произведение матриц

(ВА)С = В(АС). Левая часть равенства равна ЕС = С. Правая часть равенства равна ВЕ = В. Следовательно, В = С.

ÿ

Далее мы покажем, что левая обратная матрица В и правая обратная матрица С для А существуют Û det A ¹ 0. В этом случае мы будем называть матрицу В = С обратной матрицей для А и обозначать А^-1.

Систему линейных уравнений (4.1) запишем в матричном виде АХ = В, где А – (т,n)- матрица, основная матрица СЛУ; Х = 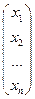- (n,1)- матрица, столбец неизвестных; В = 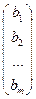- (т,1)- матрица, столбец правых частей.

Пусть Х_ч – некоторое частное решение неоднородной системы, то есть АХ_ч = В, а Х₀ – произвольное решение соответствующей однородной системы АХ = 0, то есть АХ₀ = 0

(здесь 0 в правой части – нулевой столбец). Тогда А(Х_ч+Х₀) = = АХ_ч+ АХ₀ = В + 0 = В, то есть Х₁ = Х_ч + Х₀ – также решение неоднородной системы. Наоборот, пусть Х₁ – некоторое решение неоднородной системы, то есть АХ₁ = В. Тогда

А(Х₁ - Х_ч)= АХ₁ - АХ_ч= В – В = 0, то есть Х₀ = Х₁ - Х_ч - решение однородной системы, и опять Х₁ = Х_ч + Х₀. Таким образом, все решения неоднородной СЛУ получаются из некоторого частного решения Х_ч прибавлением всевозможных решений соответствующей однородной СЛУ. Если rg A = r, то множество решений однородной СЛУ АХ= 0 является линейным пространством размерности n – r, а базисом в этом пространстве является фундаментальная система решений

f₁, f₂ ,…, f_n-r (см.7.6). Любое решение Х₀ однородной СЛУ является линейной комбинацией фундаментальной системы решений: Х₀ = a₁ f₁ +…+ a_n-rf_n-r, a₁,…,a_n-rÎ P. Выражение с₁f₁+…+ с_n-r f_n-r с произвольными постоянными с₁,…,с_n-r называется общим решением однородной СЛУ. Любое решение однородной СЛУ получается из общего решения подстановкой вместо произвольных постоянных с₁,…,с_n-r конкретных элементов поля a₁,…,a_n-r. Выражение Х_ч+ с₁ f₁ +…+ с_n-r f_n-r, где с₁,…,с_n-r - произвольные постоянные, Х_ч – некоторое частное решение неоднородной системы АХ = В, а f₁ ,…, f_n-r - фундаментальная системы решений соответствующей однородной СЛУ, является общим решением неоднородной СЛУ. И опять - любое решение неоднородной СЛУ получается из общего решения подстановкой вместо произвольных постоянных с₁ ,…, с_n-r конкретных элементов a₁,…,a_n-rÎ P.

Date: 2015-09-25; view: 382; Нарушение авторских прав