Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Упражнения. 1. Доказать, что если rk A = r , то все миноры в А порядка s, s > (r+1), равны нулю
|
|
1. Доказать, что если rk A = r, то все миноры в А порядка s, s > (r+1), равны нулю.
2. Доказать, что rk A = 0 Û A = 0.
3. Доказать, что rk A = 1 Û в А $ ненулевая строка, а все остальные строки ей пропорциональны.
Далее мы докажем, что rk A = rg A.
Утверждение. Если А – (m,n) -матрица, и А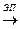 
А¢, то
rk A¢ £ rk A.
Доказательство. Пусть rk A= r. Покажем, что в матрице А¢ все миноры М¢r+1 порядка r+1 равны нулю. Отсюда и будет следовать утверждение.
Пусть А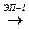 
А¢, и i- я строка матрицы А¢ получается сложением i- й строки матрицы А с j- й строкой, умноженной на сÎ Р (j¹ i). Рассмотрим минор М¢r+1 порядка r+1 в А¢. Если
i- я строка матрицы А¢ не входит в М¢r+1, то минор М¢r+1 равен соответствующему минору Мr+1 матрицы А: М¢r+1= Мr+1= 0. Если в М¢r+1 входят и i- я и j- я строки матрицы А¢, то минор М¢r+1 получается из соответствующего минора Мr+1 с помощью ЭП-I, то есть М¢r+1= Мr+1= 0. Если же i- я строка матрицы А¢ входит в М¢r+1, а j- я строка матрицы А¢ не входит в М¢r+1, то М¢r+1= Мr+1± с М0r+1,= 0± с0 = 0, где Мr+1 и М0r+1 – соответствующие миноры матрицы А.
Пусть теперь А 
А¢, и при ЭП-II в матрице А меняются местами i -я и j -я строки. Если i- я и j- я строки матрицы А¢ не входят в М¢r+1, то М¢r+1= Мr+1= 0. Если i- я и j- я строки матрицы А¢ входят в М¢r+1, то М¢r+1= - Мr+1= - 0 = 0. Если же i- я строка матрицы А¢ входит в М¢r+1, а j- я строка матрицы А¢ не входит в М¢r+1, то М¢r+1=± М0r+1 = 0, где М0r+1 - некоторый минор матрицы А.
Наконец, пусть А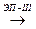 
А¢, и при ЭП-III в матрице А i- я строка умножается на сÎ Р, с ¹ 0. Если i- я строка матрицы А¢ не входит в М¢r+1, то М¢r+1= Мr+1= 0. Если же i- я строка матрицы А¢ входит в М¢r+1, то М¢r+1= с Мr+1=с 0 = 0.
ÿ
Следствие. Если А 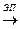А¢, то rk A¢ = rk A.
Доказательство. Так как А 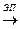А¢, то А¢ 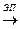А, причем
обратное ЭП - того же типа (см. упражнение 1 из 4.2). Следовательно, rk A¢ £ rk A, и rk A £ rk A¢, то есть rk A¢ = rk A.
ÿ
С помощью элементарных преобразований (как в 4.2) приведем матрицу А к ступенчатому виду
= 
.
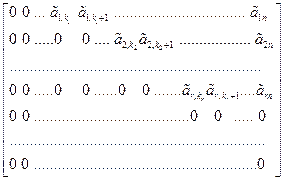Тогда rk A = rk .
Утверждение. rk = r = rg = rg A.
Доказательство. Так как в существуют лишь r ненулевых строк, то любой минор порядка r+1 содержит нулевую строку и поэтому равен нулю. Кроме того, очевидно, минор r -го порядка, стоящий на пересечении первых r строк и столбцов с номерами k1, k2,…, kr, не равен нулю – он равен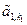 
× 
×…× 
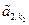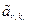¹ 0.
ÿ
Итак, мы доказали, что rk A = rg A. Далее для ранга матрицы мы будем использовать единое обозначение rg A.
Утверждение. rg At = rg A.
Доказательство. Так как определитель не меняется при транспонировании матрицы, то rk At = rk A, и
rg At = rk At = rk A = rg A.
ÿ
Последнее утверждение означает, что ранги матрицы по строкам и по столбцам совпадают, то есть размерность линейной оболочки строк матрицы и размерность линейной оболочки столбцов матрицы одинаковы.
Date: 2015-09-25; view: 894; Нарушение авторских прав