
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кинематика
|
|
Теоретическая механика
Часть 1
СТАТИКА ТВЕРДОГО ТЕЛА
КИНЕМАТИКА
Утверждено Редакционно-издательским
советом университета в качестве
учебного пособия
Краснодар
УДК 531.1/3 (075)
Д.722
Теоретическая механика. Часть 1. Статика. Кинематика: Учебное пособие / Л.И.Драйко; Кубан. гос. технол.ун-т. Краснодар, 2011. 123 с.
ISBN 5-230-06865-5
Излагается в краткой форме теоретический материал, даны примеры решения задач, большинство из которых отражает реальные вопросы техники, уделено внимание выбору рационального способа решения.
Предназначено для бакалавров заочной и дистанционной форм обучения строительных, транспортных и машиностроительных направлений.
Табл. 1 Илл. 68 Библиогр. 20 назв.
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.
Научный редактор канд.техн.наук,доц. В.Ф.Мельников
Рецензенты: зав.кафедрой теоретической механики и теории механизмов и машин Кубанского аграрного университета проф. Ф.М. Канарев; доцент кафедры теоретической механики Кубанского государственного технологического университета М.Е. Мултых
"Переиздание"
ISBN 5-230-06865-5 КубГТУ 1998г.
П Р Е Д И С Л О В И Е
Теоретическая механика является научной базой современной техники, поэтому глубокие знания теоретической механики необходимы инженеру любой специальности. Данное учебное пособие предназначено для студентов заочной формы обучения строительных, транспортных и машиностроительных специальностей, но может быть использовано студентами заочниками технологических и химико-технологических специальностей для изучения разделов "Статика твердого тела" и "Кинематика" курса теоретической механики.
Цель настоящего пособия - помочь студентам глубже разобраться в физической сущности механических взаимодействий и научить их применять методы теоретической механики к решению практических задач.
Пособие составлено в полном соответствии с действующей программой курса теоретической механики, охватывает все вопросы двух частей курса. В каждом разделе имеется краткий теоретический материал, приведены методические указания и примеры решения задач. Большое внимание уделено доходчивости изложения основных понятий и положений теоретической механики и их использование в инженерной практике.
Тематика и содержание разобранных задач отражают реальные вопросы техники и соответствуют контрольным заданиям, которые предстоит выполнить студенту заочнику при изучении курса теоретической механики.
Большое внимание уделено выбору рациональных способов решения задач, сопоставлению различных методов решения, дано подробное решение 29типовых задач.
Автор выражает глубокую признательность преподавателям кафедры теоретической механики и ТММ Кубанского аграрного университета за большой труд по рецензированию учебного пособия и подавателям кафедры теоретической механики КубГТУ за весьма ценные замечания и советы.
Все критические замечания и пожелания будут приняты автором с благодарностью и в дальнейшем.
В В Е Д Е Н И Е
Теоретическая механика изучает общие законы механического
движения и связанные с ним механические взаимодействия материальных тел.
В основу теоретической механики положены аксиомы, впервые сформулированные Ньютоном и подтвержденные многовековой практической деятельностью человека. Аксиомы механики отражают определенный уровень приближения к действительности. Пространство считается не зависящим от времени и движущейся в нем материи. Время считается универсальным, не связанным с пространством и движущейся материей.
Теоретическая механика исследует законы движения материальных точек, системы материальных точек, абсолютно твердого тела. В природе таких идеализированных тел не существует. Но абстракции, используемые в теоретической механике, позволяют найти общие законы механического движения, справедливые для движения всех физических тел. Поэтому теоретическая механика является основой большинства технических наук: теории механизмов и машин, сопротивления материалов, строительной механики, теории упругости деталей машин, гидромеханики, гидродинамики, теории колебаний и др. Большое влияние оказывает теоретическая механика на развитие автоматики, телемеханики, кибернетики и многих других дисциплин. Научные исследования по изучению космического пространства, проектированию машин и сооружений и их эксплуатации основаны на законах и методах теоретической механики.
Теоретическую механику принято делить на три части: статику, кинематику и динамику. В статике изучаются общие свойства сил и условия равновесия твердых тел. В кинематике изучаются движения тел без учета причин, вызывающих это движение. В динамике изучаются зависимости между движением материальных объектов и действующими на них силами.
Такая последовательность, изучения курса продиктована необходимостью использования математического аппарата, сложность которого возрастает постепенно, параллельно с изучением высшей математики.
I. С Т А Т И К А Т В Е Р Д О Г О Т Е Л А
1.1 ПРЕДМЕТ И ЗАДАЧИ СТАТИКИ ТВЕРДОГО ТЕЛА.
Статика - раздел теоретической механики, который изучает равновесие материальное тел под действием приложенных сил.
В статике рассматривается две основные задачи:
1) Сложение сил или приведение системы сил, действующих на твердое тело, к простейшему виду;
2) Определение условий равновесия твёрдого тела, находящегося под действием приложенных: к нему сил.
В теоретической механике рассматриваются абсолютно твердые тела. Абсолютно твердым телом называется такое тело, для которого никакие внешние воздействия не вызывают изменения размеров и формы. Расстояние между двумя точками тела всегда остается постоянным.
При взаимодействии абсолютно твердых тел изменяется характер их движения. Сила является мерой этого взаимодействия.
1.2 СИЛА. СИСТЕМА СИЛ.
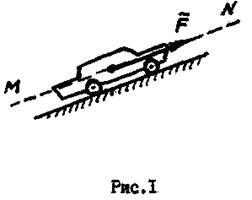
Сила является векторной величиной. Прямая MN, вдоль которой направлена сила, называется линией действия силы (рис.1).
 Характер действия силы на тело не изменяется при перемещении силы вдоль линии ее действия. Совокупность сил, действующих на твердое тело, называется системой сил. В зависимости от взаимного расположения линий действия сия существуют следующие системы сил (рис. 2).
Характер действия силы на тело не изменяется при перемещении силы вдоль линии ее действия. Совокупность сил, действующих на твердое тело, называется системой сил. В зависимости от взаимного расположения линий действия сия существуют следующие системы сил (рис. 2).
| Плоская система сходящихся сил | Плоская система параллельных сил |
| 
|
| Произвольная плоская система сил | Пространственная система сходящихся сил |
| 
|
| Система параллельных сил в пространстве | Произвольная пространственная система сил |
| 
|
Рис.2
|
 , приложенных к твердому телу, можно заменить одной силой - равнодействующей, равной геометрической сумме составляющих сил. Равнодействующей
, приложенных к твердому телу, можно заменить одной силой - равнодействующей, равной геометрической сумме составляющих сил. Равнодействующейдвух сил, приложенных в одной точке, является диагональ параллелограмма, построенного на этих силах (рис.3)
 Равнодействующая произвольного числа сходящихся сил является замыкающей стороной силового многоугольника, построенного на силах как на сторонах (рис.4):
Равнодействующая произвольного числа сходящихся сил является замыкающей стороной силового многоугольника, построенного на силах как на сторонах (рис.4):
|
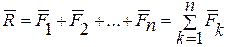 (2.3)
(2.3)
Проекцией силы на координатную ось называется скалярная величина, равная произведению модуля силы на косинус угла между вектором силы и положительным направлением оси (рис. 5):
|
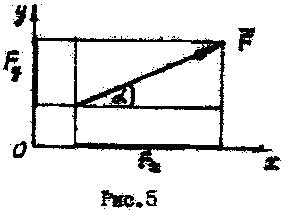
При α‹900 проекция силы на ось положительна;
При α›900 проекция силы на ось отрицательна;
При α=900 проекция силы на ось равна нулю.
При проецировании на координатные оси силы, произвольно направленной в пространстве (рис.6), необходимо предварительно спроецировать силу на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроецировать на заданную ось.
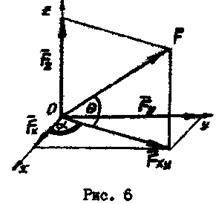
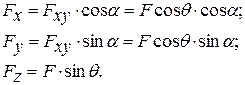 (2.7)
(2.7)
 При решении задач иногда необходимо заменить силу несколькими составляющими силами. Такая операция называется разложением силы на составляющие.
При решении задач иногда необходимо заменить силу несколькими составляющими силами. Такая операция называется разложением силы на составляющие.
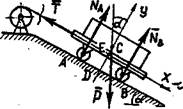
Например, на автомобиль с выключенным двигателем, находящимся на уклоне дороги (рис. 7), действует сила тяжести 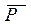 , которую можно разложить на две составляющие:
, которую можно разложить на две составляющие:
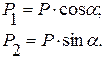
С помощью составляющих 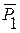 и
и 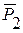 можно определить силу давления
можно определить силу давления  автомобиля на дорогу и скатывающую силу, вызывающую движение автомобиля по этому участку дороги.
автомобиля на дорогу и скатывающую силу, вызывающую движение автомобиля по этому участку дороги.
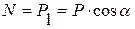
Следовательно, при разложении силы на составляющие необходимо построить параллелограммы, диагональю которого будет вектор разлагаемой силы (рис.8).
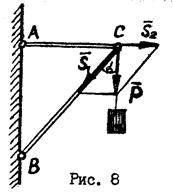 Разложить силу на две составляющие - это значит найти такие две силы, приложение которых в этой точке произведет действие, эквивалентное действию данной (разлагаемой) силы.
Разложить силу на две составляющие - это значит найти такие две силы, приложение которых в этой точке произведет действие, эквивалентное действию данной (разлагаемой) силы.
Действие силы  (веса груза) воспринимается стержнями А С и ВС. Силу
(веса груза) воспринимается стержнями А С и ВС. Силу 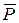 можно разложить по этим направлениям.
можно разложить по этим направлениям.
Сила, действующая на твердое тело, может быть сосредоточенной, если приложена в одной точке (рис. 9) или распределенной по длине (рис. 10), поверхности или объему данного тела.
Понятие о сосредоточенной силе является условным. Сосредоточенные силы являются равнодействующими систем распределенных сил. Сила тяжести, например, является равнодействующей сил тяжести частиц тел. Система распределенных сил характеризуется интенсивностью 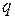 , т.е. значением силы, приходящейся на единицу длины, поверхности или объема нагруженного участка.
, т.е. значением силы, приходящейся на единицу длины, поверхности или объема нагруженного участка.
Равномерно распределенную нагрузку можно заменить сосредоточенной, приложенной в центре тяжести прямоугольника.
На рис.11 показана схема телебашни, на которую действует равномерно распределенная нагрузка интенсивностью 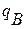 , под действием которой телебашня изгибается, а центр ее тяжестиотклоняется от исходного положения. Равнодействующую ветровой нагрузки можно определить по формуле:
, под действием которой телебашня изгибается, а центр ее тяжестиотклоняется от исходного положения. Равнодействующую ветровой нагрузки можно определить по формуле:
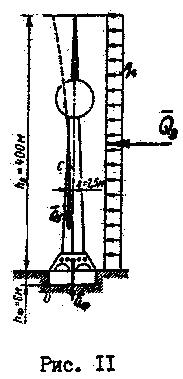
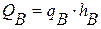
Линия действия равнодействующей проходит 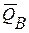 через центр тяжести прямоугольника на расстоянии, равном
через центр тяжести прямоугольника на расстоянии, равном 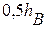 .
.
В случае распределения нагрузки по линейному закону обычно считают, что такие силы распределены по треугольнику.
Например, давление воды на стенку плотины (рис.12) зависит от глубины, т.е. от 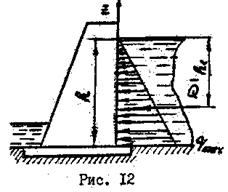 координаты Z. Равнодействующую
координаты Z. Равнодействующую  можно определить по формуле:
можно определить по формуле:
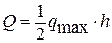
Линия действия равнодействующей лежит на расстоянии 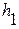 , где
, где 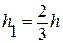 .
.
1.3. СВЯЗИ И РЕАКЦИИ СВЯЗИ.
Условия, определяющие свободу движения твердого тела, называются связями. Сила, заменяющая действие связи, называется реакцией связи. Реакции связей - силы пассивные. Задаваемые силы, приложенные к твердому телу, называются активными. Связи реализуются в виде каких-то тел, не входящих в изучаемую механическую систему. Рассмотрим основные типы связей и их реакции.
1.3.1. Гладкая опорная поверхность.
Для гладкой опорной поверхности реакция направлена по нормали к опорной поверхности соприкасающихся тел в точке их касания и приложена в этой точке (рис. 13).
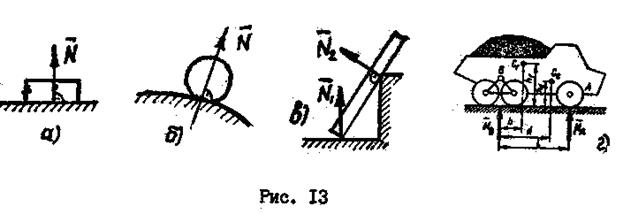
Если соприкасающиеся поверхности криволинейные, реакция связи проходит по общему перпендикуляру, проведенному через точку касания (рис.13,б). Если касание происходит в точке, реакция связи направлена по нормали к поверхности тела (рис.13,в). На рис.13,а и рис.13,г показаны реакции гладкой горизонтальной поверхности, без учета силы трения.
1.3.2. Гибкая нерастяжимая нить (трос,канат,цепь).
Гибкая нерастяжимая нить препятствует удалению тела  от точки подвеса (рис.14).
от точки подвеса (рис.14).
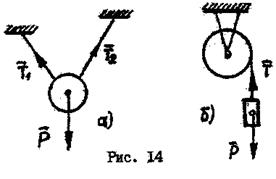 Реакция натянутой нити направлена вдоль нити к точке подвеса. Сила
Реакция натянутой нити направлена вдоль нити к точке подвеса. Сила  , с которой груз
, с которой груз  (рис.14,б) растягивает нить, называется натяжение нити.
(рис.14,б) растягивает нить, называется натяжение нити.
1.3.3. НЕВЕСОМЫЙ СТЕРЖЕНЬ.
Стержень можно считать невесомым, если его собственный вес мал по сравнению с нагрузками, которые он воспринимает. Усилие, а следовательно, и реакция стержня направлены вдоль оси, проходящей через узловые точки, которыми стержень крепится к конструкции (рис. 15).
1.3.4. ШАРНИРНОЕ СОЕДИНЕНИЕ.
Цилиндрическим шарниром называется соединение двух тел посредством пальца (болта), проходящего через отверстия в этих телах (рис. 16).
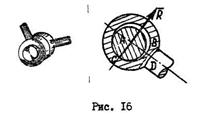 Шарнирное соединение позволяет телу только вращаться вокруг оси шарнира, перпендикулярной плоскости рисунка. Реакция шарнира должна быть направлена по общему перпендикуляру к соприкасающимся криволинейным поверхностям. Вследствие разности размеров втулки и пальца положение точки касания не определено, поэтому направление реакции цилиндрического шарнира заранее неизвестно.
Шарнирное соединение позволяет телу только вращаться вокруг оси шарнира, перпендикулярной плоскости рисунка. Реакция шарнира должна быть направлена по общему перпендикуляру к соприкасающимся криволинейным поверхностям. Вследствие разности размеров втулки и пальца положение точки касания не определено, поэтому направление реакции цилиндрического шарнира заранее неизвестно.
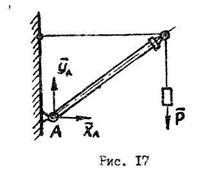
Реакцию раскладывают на две составляющие 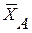 и
и 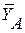 (рис. 17), лежащие в плоскости, перпендикулярной оси шарнира.
(рис. 17), лежащие в плоскости, перпендикулярной оси шарнира.
В строительстве и машиностроении в конструкциях зданий, мостов, машин, станков, транспортных средств широко используются балочные системы. Материалом для изготовления балок служит металл, железобетон, дерево. Балки воспринимают нагрузки, поперечные относительно их осей. Опорные устройства балок предназначены для передачи усилий и соединения частей конструкции.
Шарнирно-неподвижная опора (рис. 18, а) допускает поворот балки вокруг оси шарнира, но не допускает никаких линейных перемещений.
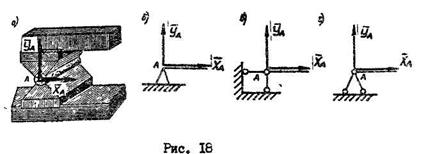
|
Опорная реакция приложена в центре шарнира, раскладывается на составляющие  и
и  . Схематическое изображение шарнирно-неподвижной опоры можно представить одним из трех вариантов, изображенных на рис. 18,б,в,г.
. Схематическое изображение шарнирно-неподвижной опоры можно представить одним из трех вариантов, изображенных на рис. 18,б,в,г.
1. 3 5. ШАРНИРНО-ПОДВИЖНАЯ ОПОРА (рис. 19, а) допускает поворот вокруг оси шарнира и линейное перемещение на небольшое расстояние вдоль опорной поверхности. Реакция такой опоры направлена перпендикулярно опорной поверхности (рис. 19, б, в, г ).
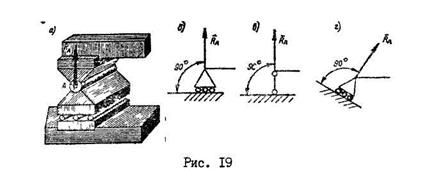
1. 3. 6. ПОДПЯТНИК И СФЕРИЧЕСКИЙ ШАРНИР закрепляют какую-либо точку тела так, что она не может совершить никаких перемещений в пространстве (рис. 20, а).
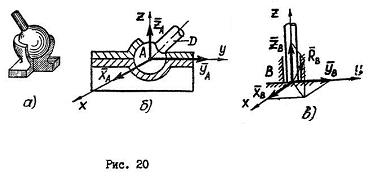
Подпятники можно рассматривать как совокупность цилиндрического шарнира и опорной поверхности, поэтому реакция связи для такой опоры раскладывается на три составляющие: (рис. 20, б)
1.3.7. ЖЕСТКАЯ ЗАДЕЛКА (ЗАЩЕМЛЕНИЕ) (рис. 21,а) не допускает ни линейных перемещений, ни поворота.
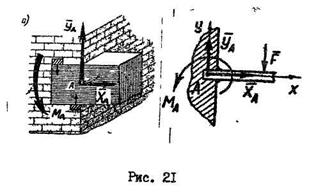 Для такой опоры не известны на только величина и направление реакции, но и точка ее приложения. Для определения опорной реакции необходимо найти три неизвестные: составляющие
Для такой опоры не известны на только величина и направление реакции, но и точка ее приложения. Для определения опорной реакции необходимо найти три неизвестные: составляющие 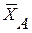 и
и 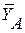 опорной реакции по осям координат и реактивного момента
опорной реакции по осям координат и реактивного момента  относительно центра тяжести опорного сечения. Второй конец балки всегда свободный, поэтому такую балку называют консольной.
относительно центра тяжести опорного сечения. Второй конец балки всегда свободный, поэтому такую балку называют консольной.
1.3.8. ПРИНЦИП ОСВОБОЖДАЕМОСТИ ОТ СВЯЗЕЙ.
Всякое несвободное тело можно рассматривать как свободное, находящееся под действием заданных сил и реакций связей.
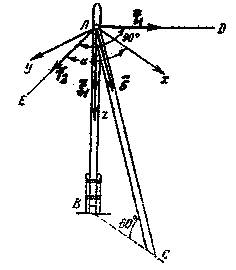
 Например, для поднимаемой ракеты весом
Например, для поднимаемой ракеты весом  (рис. 22,а) связями являются тросы АО и ОВ. Ракету можно считать свободным телом, если отбросить связи и заменить их соответствующими реакциями связей (рис. 22,б). Рассматривая условия равновесия свободного твердого тела, можно определить модули реакций связей, а по ним согласно закону равенства действия и противодействия найти давление на связи, т.е. исходные данные для расчета на прочность соответствующего элемента конструкции.
(рис. 22,а) связями являются тросы АО и ОВ. Ракету можно считать свободным телом, если отбросить связи и заменить их соответствующими реакциями связей (рис. 22,б). Рассматривая условия равновесия свободного твердого тела, можно определить модули реакций связей, а по ним согласно закону равенства действия и противодействия найти давление на связи, т.е. исходные данные для расчета на прочность соответствующего элемента конструкции.
1.4 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ (ЦЕНТРА).
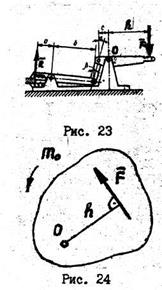
Под действием приложенной силы твердое тело может совершать не только прямолинейное перемещение, но и вращаться вокруг того или иного центра. Вращательный аффект силы характеризуется ее моментом. Например, сила 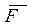 , приложенная к рукоятке рычажных механических ножниц (рис. 23), поворачивает рукоятку относительно оси
, приложенная к рукоятке рычажных механических ножниц (рис. 23), поворачивает рукоятку относительно оси 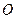 .
.
|
Моментом силы 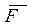 относительно центра
относительно центра 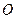 (рис. 24)называется величина, равная взятому с соответствующим знаком произведению модуля силы на кратчайшее расстояние от центра
(рис. 24)называется величина, равная взятому с соответствующим знаком произведению модуля силы на кратчайшее расстояние от центра 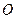 д о линии действия силы:
д о линии действия силы:
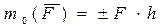 (4.1)
(4.1)
Расстояние А называется плечом силы. Момент считается положительным, если сила стремится повернуть тело относительно центра 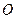 против хода часовой стрелки.
против хода часовой стрелки.
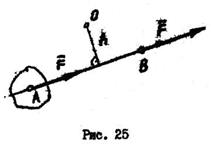 Момент силы относительно центра О не изменится, если силу перенести вдоль линии ее действия (рис. 25). Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку.
Момент силы относительно центра О не изменится, если силу перенести вдоль линии ее действия (рис. 25). Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку.
1.5 УСТОЙЧИВОСТЬ ТЕЛ ПРИ ОПРОКИДЫВАНИИ.
Рассмотрим равновесие твердого тела, находящегося под действием двух сил:  и
и  (рис. 26). Сила
(рис. 26). Сила  может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра А. Вращательный эффект сил
может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра А. Вращательный эффект сил  и
и  характеризуется моментами этих сил относительно ребра А:
характеризуется моментами этих сил относительно ребра А:
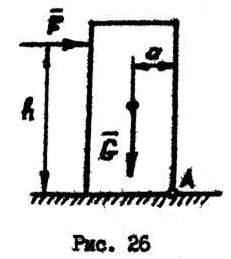
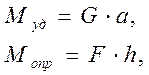
где 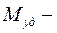 момент удерживающий;
момент удерживающий;
 момент опрокидывающий.
момент опрокидывающий.
Устойчивость при опрокидывании оценивается коэффициентом устойчивости K:
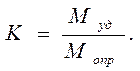
при К ›1 – состояние устойчивое;
при К =1 – имеем случай предельной устойчивости;
при К ‹1 – состояние неустойчивое.
Пример №1.
Проверить устойчивость башенного крана (рис.27) при действии ветровой нагрузки  и следующих исходных данных: вес крана с механизмами
и следующих исходных данных: вес крана с механизмами 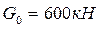 , вес противовеса
, вес противовеса  . Расчет произвести для двух случаев: при отсутствии и наличии груза весом
. Расчет произвести для двух случаев: при отсутствии и наличии груза весом 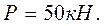
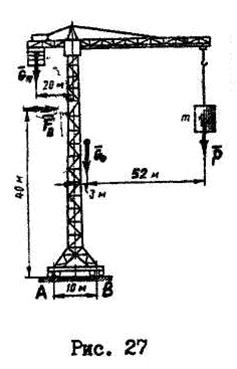
Решение:
Опрокидывание возможно при повороте вокруг оси В и отсутствии реакции в точке А.
1. При отсутствии груза:
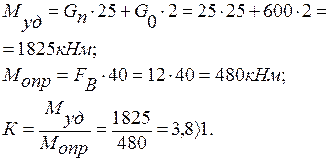
2. При наличии груза.
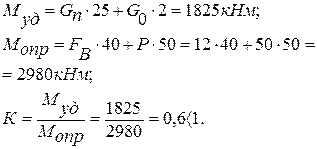
1.6. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ.
Момент силы 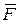 относительно оси Z характеризует вращательный эффект силы относительно этой оси (рис.28). Вращательное движение телу может сообщить только проекция силы
относительно оси Z характеризует вращательный эффект силы относительно этой оси (рис.28). Вращательное движение телу может сообщить только проекция силы 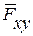 на плоскость, перпендикулярную оси (рис.29).
на плоскость, перпендикулярную оси (рис.29).

Момент силы 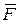 относительно оси Z равен моменту проекции этой силы на плоскость, перпендикулярную данной оси, относительно точки пересечения оси с плоскостью.
относительно оси Z равен моменту проекции этой силы на плоскость, перпендикулярную данной оси, относительно точки пересечения оси с плоскостью.
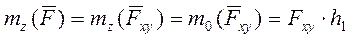 (6.1)
(6.1)
Момент силы относительно оси вполне определяется своим численным значением и знаком, т.е. является скалярной алгебраической величиной.
Момент силы относительно оси равен нулю, если сила пересекает ось или параллельна оси, т.е. сила и ось лежат в одной плоскости.
1.7 ПАРА СИЛ. МОМЕНТ ПАРЫ СИЛ.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны на некотором расстоянии d друг от друга (рис.30).
 Пара сил не имеет равнодействующей и не может быть уравновешена одной силой.
Пара сил не имеет равнодействующей и не может быть уравновешена одной силой.
Пара сил, приложенная к твердому телу, сообщает ему вращательное движение, если этому не препятствует наложенная на тело связь (рис. 31). Пара сил характеризуется плоскостью действия, направлением вращения и моментом.
Алгебраической величиной момента пары сил называется взятое с соответствующим знаком произведение модуля одной из сил пары на кратчайшее расстояние d между линиями действия сил
пары.
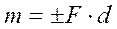 (7.1)
(7.1)
Расстояние называется плечом пары сил. Момент пары сил считается положительным, если под действием приложенной пары сил тело стремится повернуться против хода часовой стрелки. Момент пары сил можно представить в виде вектора, направленного перпендикулярно плоскости действия пары сил так, чтобы с конца этого вектора видеть поворот тела под действием пары сил в направлении, противоположном движению часовой стрелки (рис. 32).
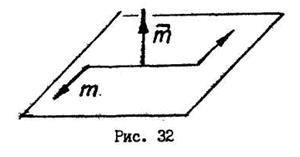 Векторы - моменты пар сил можно складывать как любые
Векторы - моменты пар сил можно складывать как любые
векторы.
1.8. ПЕРВАЯ ЗАДАЧА СТАТИКИ – приведение системы сил к простейшему виду.
Основная теорема статики гласит, что любую систему сил  (рис.33,а), действующих на абсолютно твердое тело, можно заменить совокупностью главного вектора
(рис.33,а), действующих на абсолютно твердое тело, можно заменить совокупностью главного вектора 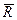 , приложенного в центре приведения
, приложенного в центре приведения 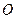 , и главного момента
, и главного момента 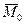 всех сил системы относительно центра приведения (рис. 33,б).
всех сил системы относительно центра приведения (рис. 33,б).
Главный вектор равен геометрической сумме всех сил, входящих в систему:
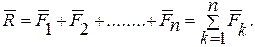 (8.1)
(8.1)
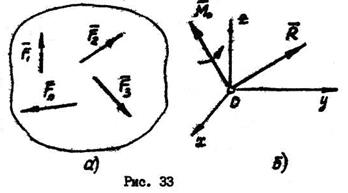 Для системы сходящихся сил главный вектор совпадает с равнодействующей.
Для системы сходящихся сил главный вектор совпадает с равнодействующей.
Главный момент системы равен геометрической сумме моментов всех сил системы относительно центра приведения:
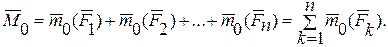 (8.2)
(8.2)
Модуль главного вектора и главного момента можно выразить через проекции на координатные оси:
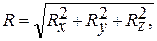 (8.3)
(8.3)
где 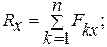
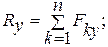
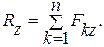 (8.4)
(8.4)
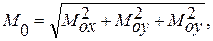 (8.5)
(8.5)
где 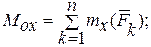
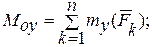
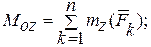 (8.6)
(8.6)
1.9. ВТОРАЯ ЗАДАЧА СТАТИКИ - определение условий равновесия твердого тела.
Твердое тело под действием приложенной системы сил будет
находиться в состоянии равновесия, если главный вектор и главный момент системы сил будут равны нулю, т.е. тело не имеет возможности дли перемещения вдоль любой координатной оси или поворота вокруг любой из осей.
Условия равновесия твердого тела в геометрической форме имеет вед
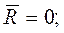
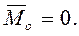 (9.1)
(9.1)
Аналитические условия равновесия твердого тела можно получить, приравняв нулю модули главного вектора и главного момента всех сил системы. Уравнения равновесия для всех частных случаев расположения сил, действующих на тело, представлены в табл. I.
Решение задач на равновесие твердого тела осуществляют в следующем порядке:
1) выделяют объект равновесия, т.е. точку или тело, равновесие
которых требуется рассмотреть;
2) к выделенному объекту равновесия прикладывают заданные силы;
3) освобождают тело или точку от связей, заменяя их реакциями
связей;
4) выбирают систему координат и составляют уравнения равновесия;
5) решая составленные уравнения равновесия, определяют искомые
величины;
6) для проверки решения составляют уравнения равновесия, не использованные в расчете; если задача решена верно, уравнение обращается в тождество.
1.10. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ.
Аналитически условия равновесия тела под действием плоской системы сходящихся сил определяются двумя уравнениями:

 (10.1)
(10.1)
| Система сил | Число уравнений равно-весия | Символическая запись уравнений равновесий | Приме-чание |
| 1.Произвольная пространственная система сил. | 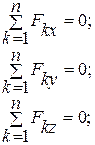 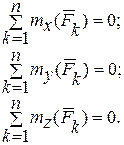
| ||
| 2.Пространствен-ная система параллельных сил. | 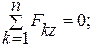 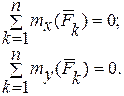
| Силы параллельны оси Z | |
| 3. Пространст-венная система сходящихся сил. | 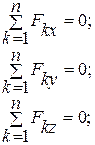
| ||
| 4. Произвольная плоская система. |  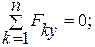  или
или
 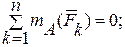 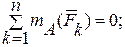 или
или
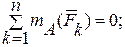 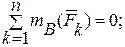 
| ось не перпендикулярна прямой АВ; точки А,В и С не лежат на одной прямой | |
| 5. Плоская система параллельных сил. | 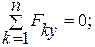
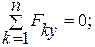
| силы параллельные оси y | |
| 6. Плоская система сходящихся сил. | 
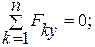
|
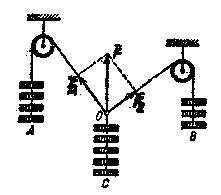
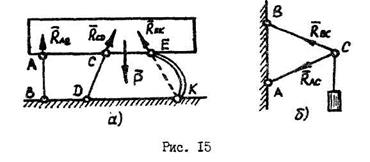
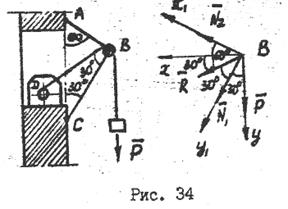
Пример №2.
Лебедкой D поднимают груз Р=10кН (рис.34). Трос перекинут через блок, укрепленный в точке В стержнями АВ и АС. Определить усилия в стержней АВ и ВС, считая крепление стержней в точках А,В и С шарнирным. Расположение стержней и троса показано на схеме.
 Решение:
Решение:
1. Выделяем узел В, равновесие которого будем рассматривать. Размерами блока В пренебрегаем. Заданными силами являются сила тяжести 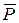 и натяжение троса
и натяжение троса  , равное силе тяжести груза.
, равное силе тяжести груза.
2. Освобождаемся от связей, заменяя их реакциями  и
и 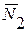 , предварительно предполагая стержни растянутыми. Систему координат выбираем с началом в точке В. Составляем уравнения равновесия плоской системы сходящихся сил:
, предварительно предполагая стержни растянутыми. Систему координат выбираем с началом в точке В. Составляем уравнения равновесия плоской системы сходящихся сил:

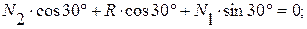 (1)
(1)
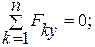
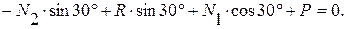 (2)
(2)
После подстановки численных значений получим систему двух уравнений:
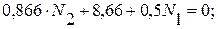 (3)
(3)
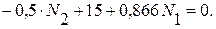 (4)
(4)
Умножив уравнение (3) на 0,5, а уравнение (4) на 0,866 и сложив полученные уравнения, получим:
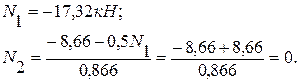
Из (3):
Знак (-) показывает, что усилие в стержне ВС – сжимающее.
Примечание. Уравнения равновесия можно получить более простыми, если оси координат 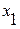 и
и 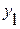 направить вдоль стержней АВ и АС:
направить вдоль стержней АВ и АС:
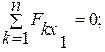
 (5)
(5)

 (6)
(6)
Из (5) с учетом того, что R=P, получим N2 =0;
Из (6): 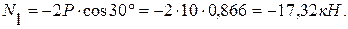
1.11. ПЛОСКАЯ СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ.
Равновесие плоской системы сил, параллельных оси Y, можно записать следующим образом:
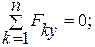
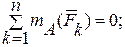 (11.1)
(11.1)
или 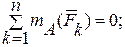
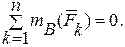 (11.2)
(11.2)
При этом точки А и В не должны лежать на прямой, параллельной линиям действия сил.
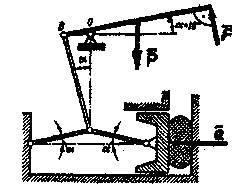
Пример №3.
Поворотный кран предназначен для подъема груза P=12кН. Определить опорные реакции при следующих исходных данных:
вес колонны: 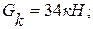
вес тележки: 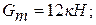
вес тележки вес привода подъема: 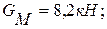
вес привода поворота: 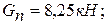
интенсивность распределенной нагрузки: 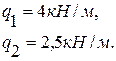
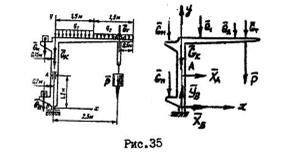 Решение:
Решение:
1.Рассматриваем равновесие поворотного крана. Заданными силами являются силы тяжести: 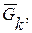
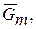
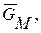
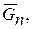
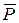 , распределенная нагрузка интенсивностью
, распределенная нагрузка интенсивностью 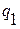 и
и 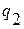 .
.
2. Равномерно распределенную нагрузку заменяем сосредоточенной:
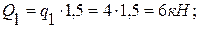
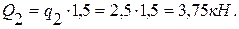
Равнодействующие  и
и 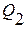 распределенной нагрузки прикладываем в середине основания соответствующих прямоугольников.
распределенной нагрузки прикладываем в середине основания соответствующих прямоугольников.
3. Освобождаемся от связей, заменяя их реакциями. Так как к поворотному крану приложена плоская система сил, реакция подшипника А будет представлена одной составляющей 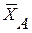 , а подпятника В – составляющими
, а подпятника В – составляющими 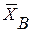 и
и 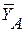 . При составлении уравнения моментов за моментную точку принимаем точку В, через которую проходят линии действия двух неизвестных величин
. При составлении уравнения моментов за моментную точку принимаем точку В, через которую проходят линии действия двух неизвестных величин 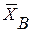 и
и 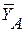 .
.
С учетом выбранной системы координат составляем уравнения равновесия:
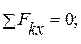
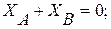 (1)
(1)
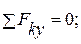
 (2)
(2)
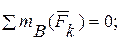 (3)
(3)
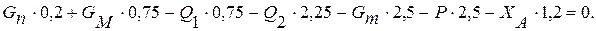
Решая систему уравнений (1)-(3), находим:
из (2): 
из (3): 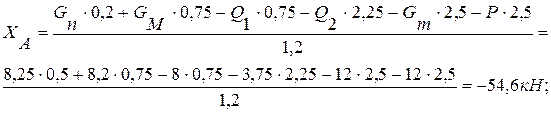
из (1): 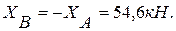
Для проверки составим уравнение моментов относительно точки А:
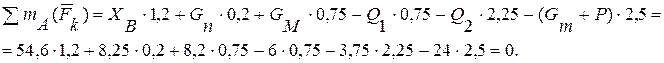 Следовательно, задача решена правильно.
Следовательно, задача решена правильно.
1.12. ТЕОРЕМА ВАРИНЬОНА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ.
Систему, сходящихся сил, приложенных к твердому телу, можно привести к равнодействующей (см. раздел 2). Момент равнодействующей относительно любого центра или оси равен алгебраической сумме моментов составляющих сил относительно того же центра или оси (теорема Вариньона).
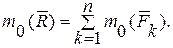 (12.1)
(12.1)
Эту теорему часто используют при решении задач. Пусть, например, требуется определить момент силы 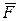 относительно точки А (рис.36). Силу
относительно точки А (рис.36). Силу 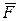 можно разложить на составляющие
можно разложить на составляющие 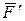 и
и 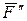 ,где
,где
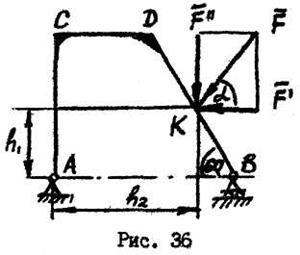

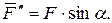
Тогда
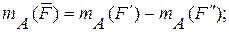
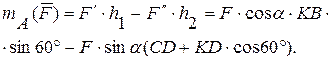
1.13. ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ.
Условия равновесия произвольной плоской системы сил можно определить тремя уравнениями:

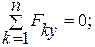
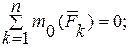 (13.1)
(13.1)
Другие варианты уравнений равновесия приведены в таблице.1.
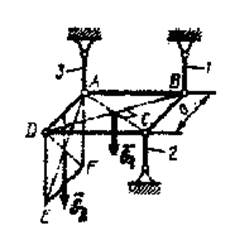
Пример №4.
Определить опорные реакции жесткой рамы (рис.37), закрепленной в точке А шарнирно, а в точке В прикрепленной к невесомому стержню. На раму действует пара сил с моментом М, силы  и
и 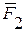 натяжение троса под действием груза
натяжение троса под действием груза 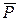 .
.
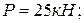
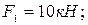
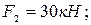
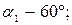
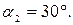
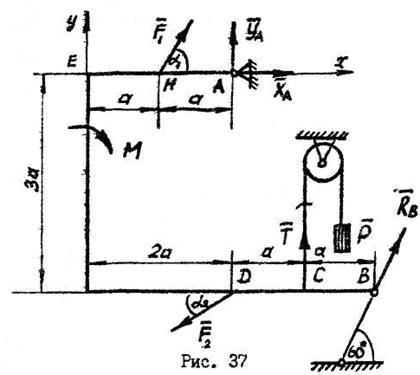 Решение:
Решение:
1.Рассматриваем равновесие жесткой рамы, находящейся под действием заданных сил  ,
,  и пары с моментом
и пары с моментом  . Натяжение троса
. Натяжение троса  равно весу груза
равно весу груза  .
.
2. Освобождаем раму от связей, заменяя их реакциями. Реакции шарнирно-неподвижной опоры А раскладываем на 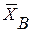 и
и 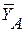 .
.
Реакции невесомого стержня, к которому рама крепиться в точке В, направлена вдоль стержня.
3. Выбираем систему координат и составляем уравнения равновесия для рамы, находящейся под действием плоской системы сил. Уравнение моментов составляем относительно точки А, где пересекаются линии действия неизвестных реакций 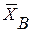 и
и 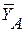 . При вычислении моментов сил
. При вычислении моментов сил  ,
, 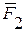 и реакции
и реакции 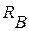 относительно точки А используем теорему Вариньона. Составляющими сил
относительно точки А используем теорему Вариньона. Составляющими сил  и
и 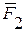 являются проекции этих сил на координатные оси.
являются проекции этих сил на координатные оси.
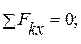
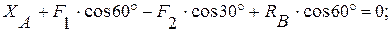 (1)
(1)
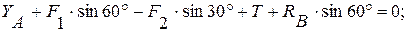 (2)
(2)
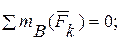 (3)
(3) 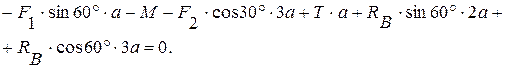
Находим из (3): 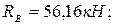
из (1): 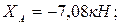
из (2): 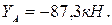
Действительное направление реакций 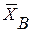 и
и 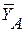 противоположно показанному на чертеже.
противоположно показанному на чертеже.
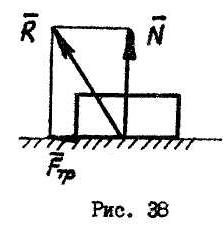
1.14. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ.
Если тело находится в равновесии на шероховатой поверхности, полная реакция 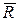 такой опорной поверхности будет представлена двумя составляющими: нормальным давлением
такой опорной поверхности будет представлена двумя составляющими: нормальным давлением 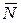 и силой трения
и силой трения 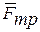 (рис. 38). Величина предельной силы трения не зависит от размеров соприкасающихся поверхностей:
(рис. 38). Величина предельной силы трения не зависит от размеров соприкасающихся поверхностей:
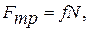 (14.1)
(14.1)
где 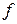 - коэффициент трения скольжения, зависящий от материала и состояния соприкасающихся поверхностей. В уравнения равновесия твердого тела, находящегося на шероховатой поверхности, кроме сил заданных и реакций связей будет входить сила трения.
- коэффициент трения скольжения, зависящий от материала и состояния соприкасающихся поверхностей. В уравнения равновесия твердого тела, находящегося на шероховатой поверхности, кроме сил заданных и реакций связей будет входить сила трения.
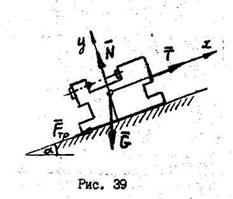
Пример №5.
Станок весом 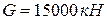 передвигают по деревянному настилу с углом подъема
передвигают по деревянному настилу с углом подъема 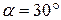 при помощи лебедки (рис.39). Определить натяжение троса, если коэффициент трения стали по дереву
при помощи лебедки (рис.39). Определить натяжение троса, если коэффициент трения стали по дереву 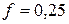 .
.
 Решение:
Решение:
1. Рассматриваем равновесие станка, находящегося на наклонной плоскости под действием силы тяжести  , натяжением троса
, натяжением троса  , составляющих реакций шероховатой поверхности
, составляющих реакций шероховатой поверхности 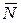 и
и 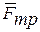 . При равномерном подъеме все эти силы должны находиться в равновесии. Величину нормального давления определим, проецируя все силы на ось Y:
. При равномерном подъеме все эти силы должны находиться в равновесии. Величину нормального давления определим, проецируя все силы на ось Y:

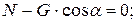
откуда 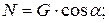
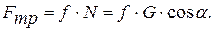
2. Уравнение равновесия тела составляем в проекции на ось X:
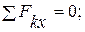

откуда
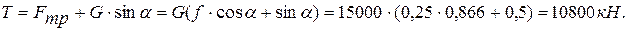
1.15. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ КАЧЕНИЯ.
При перекатывании одной криволинейной поверхности по другой возникает сопротивление, называемое трением качения. Если к катку приложить силу  (рис. 40), то вследствие деформации поверхности в месте контакта линия действия силы нормального давления
(рис. 40), то вследствие деформации поверхности в месте контакта линия действия силы нормального давления 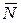 проходит на некотором расстоянии К от оси
проходит на некотором расстоянии К от оси 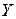 Максимальную величину К, соответствующую предельному положению равновесия, называют коэффициентом трения качения. Силы
Максимальную величину К, соответствующую предельному положению равновесия, называют коэффициентом трения качения. Силы 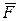 и
и 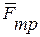 образуют пару сил, стремящуюся повернуть каток. Силы
образуют пару сил, стремящуюся повернуть каток. Силы  и
и  образуют пару сил с моментом, препятствующим повороту катка. Момент этой пары
образуют пару сил с моментом, препятствующим повороту катка. Момент этой пары
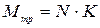 (15.1)
(15.1)
называют моментом трения качения. Трение качения возникает только при перекатывании упругих тел. Для качения абсолютно твердого катка по абсолютно твердой не деформируемой поверхности не потребуется никакой силы.
Если  , то скольжение невозможно,
, то скольжение невозможно,
если 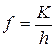 , то проходит одновременно скольжение и качение,
, то проходит одновременно скольжение и качение,
если 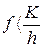 , то качение невозможно.
, то качение невозможно.
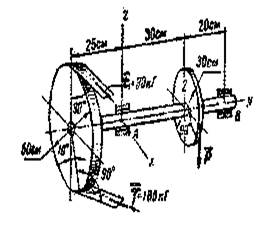
Пример №6.
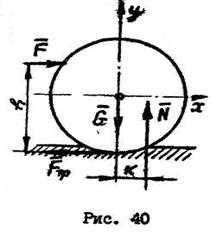 Для равномерного передвижения по горизонтальному деревянному настилу станка (рис. 41) весом
Для равномерного передвижения по горизонтальному деревянному настилу станка (рис. 41) весом 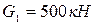 использовали 10 стальных катков диаметром
использовали 10 стальных катков диаметром 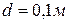 и весом
и весом 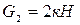 каждый. Определить необходимое горизонтальное движущее усилие
каждый. Определить необходимое горизонтальное движущее усилие 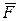 , если коэффициент трения качения стали по чугуну
, если коэффициент трения качения стали по чугуну 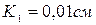 , а стали по дереву
, а стали по дереву 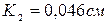 .
.
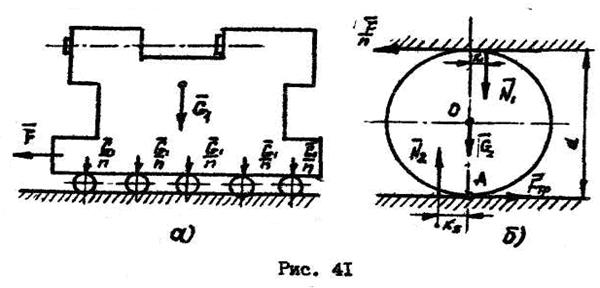
Решение:
1. Считаем, что на каждый каток приходится одинаковая часть веса станины 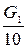 . Рассматриваем равновесие одного катка (рис. 41,б) под действием активных сил и реакций связей: силы тяжести
. Рассматриваем равновесие одного катка (рис. 41,б) под действием активных сил и реакций связей: силы тяжести  , нормальных реакций
, нормальных реакций 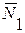 и
и 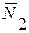 , движущей силы
, движущей силы  на один каток и силы трения скольжения со стороны пола. Составим уравнение равновесия:
на один каток и силы трения скольжения со стороны пола. Составим уравнение равновесия:
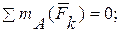
 (1)
(1)

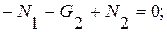 (2)
(2)
где 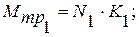
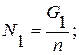
 (3)
(3)
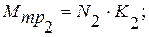
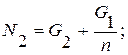
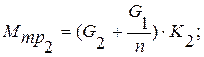 (4)
(4)
Подставим (3) и (4) в (1):
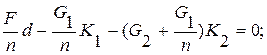
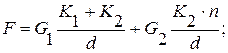
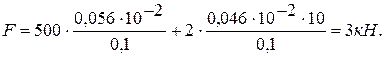
1.16. СТАТИЧЕСКИ ОПРЕДЕЛЕННЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ.
Для каждого случая нагружения твердого тела можно составить определенное число независимых уравнений. Если числа уравнений достаточно для определения неизвестных величин, система называется статически определимой, в противном случае – статически неопределимой. Если арка (рис.42) нагружена силами  , то направления реакций в опорах А и В неизвестны, каждая из них будет представлена двумя составляющими. Следовательно, количество неизвестных (
, то направления реакций в опорах А и В неизвестны, каждая из них будет представлена двумя составляющими. Следовательно, количество неизвестных ( ) превышает число независимых уравнений равновесия для плоской системы сил, т.е. плоская система является статически неопределимой.
) превышает число независимых уравнений равновесия для плоской системы сил, т.е. плоская система является статически неопределимой.
1.17. РАВНОВЕСИЕ СОСТАВНОЙ КОНСТРУКЦИИ ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ.
Системой сочлененных тел называется несколько твердых тел, соединенных между собой посредством шарниров, стержней или нитей. Связи, соединяющие части составной конструкции, называются внутренними, в отличие от внешних связей, соединяющих конструкцию о опорами. Для каждого тела, входящего в составную конструкцию, находящуюся под действием плоской системы сил, можно составить три уравнения равновесия. Следовательно, общее число уравнений равновесия для составной конструкции равно 3n, где n - число тел, образующих систему.
Задачи на равновесие составных конструкций рекомендуется решать в следующем порядке:
1) выделить составную конструкцию, равновесие которой рассматривается;
2) изобразить заданные силы, действующие на систему тел;
3) отбросить внешние связи, заменив их реакциями;
4) выбрать систему координат;
5} определить пути решения задачи: рассматривать равновесие каждой части конструкции в отдельности или равновесие системы в целом и одной из частей конструкции; прежде всего следует рассматривать те части составной конструкции, для которых из составленных уравнений равновесия можно определить искомые величины;
6) решить составленную систему уравнений равновесия относительно неизвестных величин;
7) проверить правильность решения, составляя неиспользованные в расчете уравнений равновесия для всей, конструкции.
Пример №7.
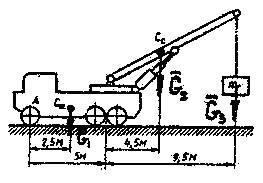
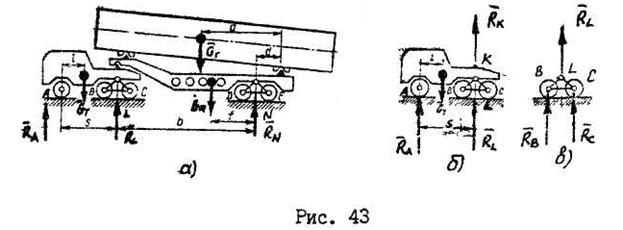
Определить нагрузку на каждую из пяти (А, В, С, D, E) осей автотягача с седельным полуприцепом (рис.43).
Решение:
Автотягач состоит из трех частей: шасси весом 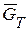 , полуприцепа весом
, полуприцепа весом 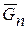 и кузова весом
и кузова весом 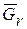 . Рассмотрим равновесие одной части конструкции – шасси (рис. 43,б). Действие отброшенной части заменим реакцией связи
. Рассмотрим равновесие одной части конструкции – шасси (рис. 43,б). Действие отброшенной части заменим реакцией связи 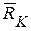 . Реакциями внешних связей для шасси являются
. Реакциями внешних связей для шасси являются 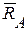 и
и 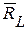 . Для нахождения реакции
. Для нахождения реакции 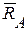 составим сумму моментов относительно точки
составим сумму моментов относительно точки 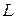 :
:
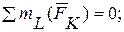
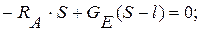 (1)
(1)
Откуда 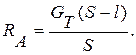 (2)
(2)
Рассматривая равновесие составной конструкции (рис. 43,а), найдем реакции остальных внешних связей 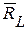 и
и 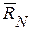 :
:
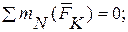
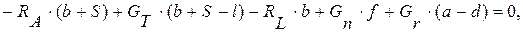 (2)
(2)
Откуда с учетом (2) выразим:
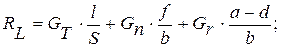 (3)
(3)

 (4)
(4)
откуда с учетом (3) выразим:
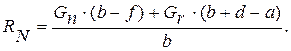 (4)
(4)
Учитывая симметричный характер нагрузки на оси (рис.43,в), определим реакции:
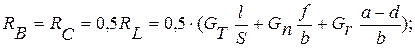
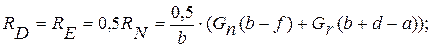
Пример №8.
Определить реакции внешних и внутренних связей конструкции, состоящей из жесткого угольника и стержня (рис.44), соединенных шарнирно в точке С. На составную конструкцию действуют силы 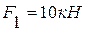 и
и  , равномерно распределенная нагрузка интенсивностью
, равномерно распределенная нагрузка интенсивностью 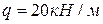 , пара сил с моментом
, пара сил с моментом 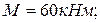
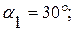


|
Решение:
Внешними связями, наложенными на конструкцию, является жесткая заделка в точке А и свободное опирание на гладкую поверхность в точке В. Внутренней связью является шарнирно С, с помощью которого соединены между собой части конструкции в отдельности, начиная расчет с равновесия стержня, у которого неизвестны три реакции связей  ,
, 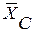 и
и 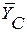 . Действие равномерно распределенной нагрузки интенсивностью
. Действие равномерно распределенной нагрузки интенсивностью 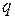 заменим сосредоточенной силой
заменим сосредоточенной силой  :
:

Выбираем систему координат и составляем три уравнения равновесия для стержня ВС:
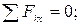
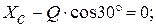 (1)
(1)
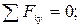
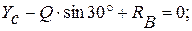 (2)
(2)
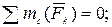
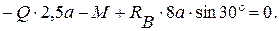 (3)
(3)
из (1): 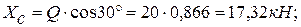
из (2): 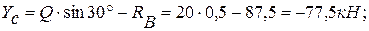
из (3): 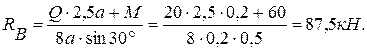
Действительное направление реакции 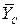 противоположно показанному на чертеже. Рассматриваем равновесие левой части конструкции. Составляющие реакции внутренней связи
противоположно показанному на чертеже. Рассматриваем равновесие левой части конструкции. Составляющие реакции внутренней связи  и
и 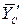 направлены в стороны, противоположные направлениям составляющих
направлены в стороны, противоположные направлениям составляющих 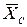 и
и 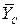 .
.
Составим три уравнения равновесия для левой части конструкции:
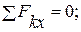
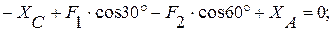 (4)
(4)
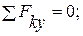
 (5)
(5)
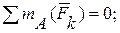
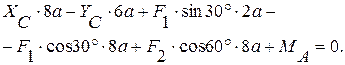 (6)
(6)
из (4):
Date: 2015-09-24; view: 1029; Нарушение авторских прав
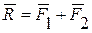 (2.1)
Модуль равнодействующей
(2.1)
Модуль равнодействующей
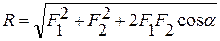 (2.2)
(2.2)
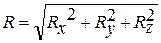 (2.4)
где
(2.4)
где
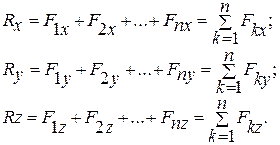 (2.5)
(2.5)
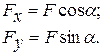 (2.6)
(2.6)