
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примерный перечень вопросов к экзамену. 1. Сравнение бесконечных множеств
|
|
1. Сравнение бесконечных множеств. Равномощные и неравномощные множества. Понятие мощности множества.
2. Счётные множества и их свойства. Счётность множеств рациональных и алгебраических чисел.
3. Несчётность отрезка числовой прямой и множества действительных чисел. Множества мощности континуум.
4. Мощность множества подмножеств. Существование множеств сколь угодно большой мощности.
5. Континуальность множества подмножеств счётного множества.
6. Сравнение мощностей. Теорема Кантора-Бернштейна. Понятие о трансфинитном ряде мощностей.
7. Замкнутые и открытые множества на прямой, их свойства.
8. Совершенные множества. Строение открытых и замкнутых множеств.
9. Канторово совершенное множество.
10. Мощность замкнутых и совершенных множеств.
11. Мера открытых и замкнутых множеств на прямой.
12. Множества, измеримые по Лебегу.
13. Теоремы об измеримых множествах.
14. Функции, измеримые по Лебегу, их свойства.
15. Интеграл Лебега от ограниченной функции и его основные свойства.
16. Сравнение интегралов Римана и Лебега. Критерий интегрируемости по Риману ограниченной функции.
17. Определение метрического пространства. Понятие окрестности точки. Сходящиеся последовательности точек. Фундаментальные последовательности.
18. Примеры метрических пространств.
19. Замкнутые и открытые множества в метрическом пространстве, их свойства.
20. Полные метрические пространства. Полнота пространств Rn и  .
.
21. Операторы и функционалы. Предел и непрерывность отображений.
22. Сжимающие отображения метрического пространства в себя. Теорема Банаха о неподвижной точке.
23. Понятие гильбертова пространства. Критерий полноты ортогональной системы в гильбертовом пространстве.
24. Ряды Фурье в гильбертовых пространствах.
СПИСОК Рекомендуемой литературы
основной
1. Вулих, Б.З. Введение в функциональный анализ / Б.З. Вулих. – М.: Наука, 1967.
2. Вулих, Б.З. Краткий курс функций вещественной переменной / Б.З. Вулих. – М.: Наука, 1973.
3. Колмогоров, А.Н. Элементы теории функций и функционального анализа / А.Н. Колмогоров, С.В. Фомин. – М.: Наука, 1976.
4. Макаров, И.П. Дополнительные главы математического анализа / И.П. Макаров. – М.: Просвещение, 1968.
5. Натансон, И.И. Теория функций вещественной переменной / И.И. Натансон. – М.: Наука, 1974.
6. Очан, Ю.С. Сборник задач по математическому анализу / Ю.С. Очан. – М.: Просвещение, 1981.
дополнительный
1. Антоневич, А.Б. Задачи и упражнения по функциональному анализу / А.Б. Антоневич, П.Н. Князев, Я.В. Радыно. – Минск: Вышэйшая школа, 1978.
2. Люстерник, Л.А., Элементы функционального анализа / Л.А. Люстерник, В.И. Соболев. – М.: Наука, 1965.
3. Соболев, В.И. Лекции по дополнительным главам математического анализа / В.И. Соболев. – М.: Наука, 1968.
4. Теляковский, С.А. Сборник задач по теории функций действительного переменного / С.А. Теляковский. – М.: Наука, 1980.
5. Треногин, В.А. Задачи и упражнения по функциональному анализу / В.А. Треногин, Б.М. Писаревский, Т.С.Соболева. – М.: Наука, 1984.
ОТВЕТЫ И РЕШЕНИЯ
1. 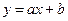 ,
, 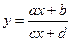 ,
, 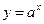 ,
, 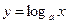 ,
, 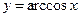 ,
, 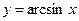 ,
, 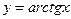 ,
, 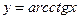 .
.
2. a)  ;
;
б) Указание. См. пункт а);
в) 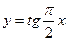 .
.
3. Первая – да; вторая – нет.
4. Пусть φ – не является взаимно однозначным отображением, т.е. 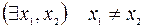 такие, что
такие, что 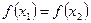 . Но тогда y = f(x) не строго монотонна, что противоречит условию.
. Но тогда y = f(x) не строго монотонна, что противоречит условию.
5. Так как в точке х0 экстремум функции, то в окрестности (х0 – δ; х0 + δ) 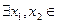 (х0 – δ; х0 + δ) такие, что
(х0 – δ; х0 + δ) такие, что 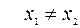 , но
, но 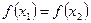 . Последнее равенство показывает, что отображение функцией y = f(x) не является взаимно однозначным.
. Последнее равенство показывает, что отображение функцией y = f(x) не является взаимно однозначным.
6. а) Нет, так как непрерывная функция отображает отрезок [ a;b ] в отрезок [ m; M ], где m = inf{f(x)}, M = sup{f(x)}.
б) Нет, так как значения непрерывной функции, заданной на отрезке [ a;b ], сплошь заполняют отрезок [ m;M ].
12. Так как отображение φ: A → C – взаимно однозначное, то А ~ С и В ~ φ(В). Откуда следует, что А \ В ~ С \ φ(В).
13. Выделим на интервале (0;1) множество М = 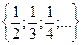 , а на отрезке [0;1] выделим множество K =
, а на отрезке [0;1] выделим множество K = 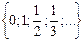 . Установим следующее соответствие:
. Установим следующее соответствие:
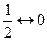 ,
, 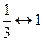 ,
, 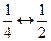 ,
, 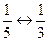 , …,
, …,  , …; n ≥3 (см. рис. 2).
, …; n ≥3 (см. рис. 2).
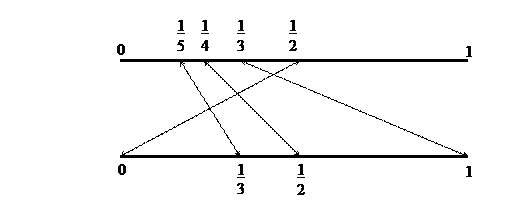
Рис. 2
Всем остальным точкам интервала (0;1) поставим в соответствие точки отрезка [0;1] с теми же координатами. Тогда M ~ K и (0;1)\M ~ [0;1]\K, откуда (0;1) ~ [0;1].
14. а) Результат предыдущей задачи: (0;1) ~ [0;1]. С помощью функции y = ctgπx взаимно однозначно отобразим интервал (0;1) на действительную ось (-∞;+∞). Значит [0;1] ~ (0;1) ~ (- ∞;+∞). Отсюда по свойству транзитивности отношения эквивалентности: [0;1] ~ (- ∞;+∞).
б) Взаимно однозначно отобразим [0;+∞) на [0;1) с помощью функции 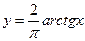 ; затем методом решения задачи №13 полуинтервал [0;1) отобразим на интервал (0;1). Наконец, с помощью линейной функции отобразим (0;1) на (a;b).
; затем методом решения задачи №13 полуинтервал [0;1) отобразим на интервал (0;1). Наконец, с помощью линейной функции отобразим (0;1) на (a;b).
15. Рекомендуется установить взаимно однозначное соответствие между множествами или применить свойства эквивалентных множеств.
17. Выделим на множестве I (иррациональных чисел) некоторое подмножество 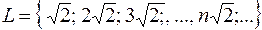 . Множество всех остальных иррациональных чисел, не входящих в это множество, обозначим С. Тогда I = L
. Множество всех остальных иррациональных чисел, не входящих в это множество, обозначим С. Тогда I = L  C, причем L∩C = Ø. Множество действительных чисел R = I
C, причем L∩C = Ø. Множество действительных чисел R = I  Q, где Q – множество рациональных чисел. Так как I = L
Q, где Q – множество рациональных чисел. Так как I = L  C, то R = C
C, то R = C  (L
(L  Q).
Q).
Установим взаимно однозначное соответствие между L  Q и L следующим образом:
Q и L следующим образом:
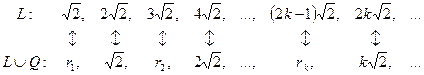
Тогда L ~ L  Q, C ~ C. Используя результаты задачи №8, получим, что I ~ R.
Q, C ~ C. Используя результаты задачи №8, получим, что I ~ R.
18. Z = N–  {0}
{0}  N. Множество N– = {–1, –2, –3, …} эквивалентно множеству N, следовательно,
N. Множество N– = {–1, –2, –3, …} эквивалентно множеству N, следовательно, 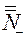 = a. Тогда
= a. Тогда 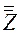 = a+1+a = a.
= a+1+a = a.
19. 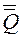 = а.
= а.
20. Пусть М – множество точек плоскости с рациональными координатами, т.е. М = {(ai, bi)}. Зафиксируем bi, получим подмножество М i множества М, 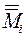 = a. Так как М =
= a. Так как М = 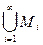 , то
, то 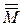 = а + а + … = а.
= а + а + … = а.
21. Задача решается аналогично предыдущей задаче.
22. 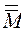 = а.
= а.
23. а.
24. Элементами исследуемого множества являются многочлены 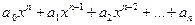 , где аi – целые числа (i = 0, 1, 2, …). Зафиксируем n и найдем мощность множества Mn – многочленов n -ой степени. Mn эквивалентно множеству наборов из n целых чисел: { a0; a1; …; an }, следовательно,
, где аi – целые числа (i = 0, 1, 2, …). Зафиксируем n и найдем мощность множества Mn – многочленов n -ой степени. Mn эквивалентно множеству наборов из n целых чисел: { a0; a1; …; an }, следовательно,
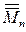 = a. Так как М =
= a. Так как М = 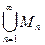 , то
, то 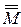 = а + а + … = а.
= а + а + … = а.
25.  = а (см. решение задачи №24).
= а (см. решение задачи №24).
26. 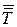 = с, так как Т = R \ A
= с, так как Т = R \ A 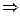
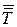 = с – a = c.
= с – a = c.
27. 
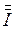 = с, так как I = R \ Q
= с, так как I = R \ Q 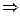
 = с – a = c.
= с – a = c.
28. Пусть М – множество интервалов с рациональными концами. М эквивалентно множеству пар рациональных чисел. Последнее множество имеет мощность а (см. задачу №20), следовательно,  = а.
= а.
29. M = {(a; b)}, причем, если (a; b) и (c; d) принадлежат М, то
(a; b) 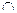 (c; d) = Ø. В силу плотности множества действительных чисел в любом интервале найдется рациональная точка. Следовательно, М эквивалентно некоторому подмножеству множества рациональных чисел. Откуда,
(c; d) = Ø. В силу плотности множества действительных чисел в любом интервале найдется рациональная точка. Следовательно, М эквивалентно некоторому подмножеству множества рациональных чисел. Откуда, 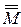
 а.
а.
30. Множество М локальных экстремумов функции 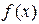 эквивалентно множеству попарно непересекающихся интервалов, последнее не более чем счетно (см. задачу №29). Следовательно,
эквивалентно множеству попарно непересекающихся интервалов, последнее не более чем счетно (см. задачу №29). Следовательно, 
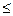 а.
а.
32. Обозначим через Аi – множество точек разрыва на отрезке [- i; i ]. Покажем, что множество Ai не более чем счетно. Предположим, что f(x) монотонно возрастает. Пусть х 0 – точка разрыва f (x), х0  [- i; i ]. Так как f(x) – монотонна, то х 0 – точка разрыва 1-го рода. Назовем разность f(х0+0) – f(х0-0) скачком функции в точке х 0. Для монотонно возрастающей функции
[- i; i ]. Так как f(x) – монотонна, то х 0 – точка разрыва 1-го рода. Назовем разность f(х0+0) – f(х0-0) скачком функции в точке х 0. Для монотонно возрастающей функции
f(х0+0) – f(х0-0) > 0. Число точек разрыва на [- i; i ], в которых скачок больше α, не больше, чем 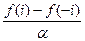 .
.
Обозначим через Ек множество точек разрыва со скачком больше 
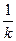 . Тогда множество всех точек разрыва на отрезке [- i; i ] есть Аi =
. Тогда множество всех точек разрыва на отрезке [- i; i ] есть Аi = 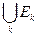 . Множество Ек – конечно, тогда Аi – не более чем счетно. Множество А всех точек разрыва на числовой прямой есть А =
. Множество Ек – конечно, тогда Аi – не более чем счетно. Множество А всех точек разрыва на числовой прямой есть А = 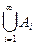 , следовательно,
, следовательно, 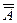
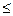 а.
а.
34. Каждая точка плоскости может быть представлена как элемент множества { 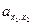 }, где х1 и х2 независимо друг от друга принимают с значений. Поэтому с – мощность искомого множества.
}, где х1 и х2 независимо друг от друга принимают с значений. Поэтому с – мощность искомого множества.
36. Пусть А – множество монотонно возрастающих непрерывных функций. В – множество непрерывных функций. М – множество функций { y= kx }, где k  R и k>1. Так как k
R и k>1. Так как k  (1,+∞), то
(1,+∞), то  = с.
= с.
М  А
А 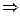
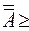 с (1).
с (1). 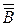 = с (см. задачу №35). А
= с (см. задачу №35). А 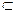 В
В 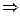
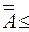 с (2).
с (2).
Из (1) и (2) следует:  = с.
= с.
37. а.
38. Так как мощность множества всех подмножеств счетного множества есть 2 а = с, а мощность всех конечных подмножеств счетного множества равна а, то мощность множества всех бесконечных подмножеств счетного множества равна с– а = с.
41. а) 0; б) {0; 1}; в) Ø; г) [-1; 2]; д) Ø.
45. Предположим, что Е имеет предельные точки, и пусть ξ одна из них. Выберем ε < 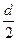 , тогда в ε-окрестности точки ξ содержится бесконечно много точек множества Е. Пусть х1 и х2 две такие точки. Тогда d
, тогда в ε-окрестности точки ξ содержится бесконечно много точек множества Е. Пусть х1 и х2 две такие точки. Тогда d  ρ(x1,x2)
ρ(x1,x2) 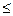 ρ(x1, ξ) +
ρ(x1, ξ) +
+ ρ(ξ ,x2)< 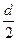 +
+ 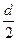 = d, т.е. d < d, что невозможно. Следовательно, Е не имеет предельных точек.
= d, т.е. d < d, что невозможно. Следовательно, Е не имеет предельных точек.
46. Пусть x0 – предельная точка Е′. Тогда в любой ε-окрестности точки x0 содержится бесконечное множество точек Е′. Пусть z – такая точка, z  S(x0, ε). Так как z
S(x0, ε). Так как z  Е′, она является предельной точкой множества Е, значит в этой же окрестности содержится бесконечное множество точек Е. Так как S (x0, ε) – окрестность точки х0, содержащая бесконечное множество точек из Е, то х0 – предельная точка Е и, следовательно, х0
Е′, она является предельной точкой множества Е, значит в этой же окрестности содержится бесконечное множество точек Е. Так как S (x0, ε) – окрестность точки х0, содержащая бесконечное множество точек из Е, то х0 – предельная точка Е и, следовательно, х0  Е′. В силу произвольности точки x0 последнее означает, что множество Е′ замкнуто.
Е′. В силу произвольности точки x0 последнее означает, что множество Е′ замкнуто.
47. Так как Е замкнуто, то Е′ 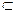 Е, тогда
Е, тогда 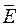 = Е
= Е  Е′ = Е.
Е′ = Е.
48. а) Чтобы доказать равенство (А  В)′ = А′
В)′ = А′  В′, нужно доказать два включения: (А
В′, нужно доказать два включения: (А  В)′
В)′  А′
А′  В′ и (А
В′ и (А  В)′
В)′  А′
А′  В′.
В′.
Пусть х0  (А
(А  В)′, тогда или х 0 – предельная точка множества А, т.е. х0
В)′, тогда или х 0 – предельная точка множества А, т.е. х0  А′, или х0 – предельная точка множества В, т.е. х0
А′, или х0 – предельная точка множества В, т.е. х0  В′. Отсюда следует, что х0
В′. Отсюда следует, что х0  А′
А′  В′. Первое включение (А
В′. Первое включение (А  В)′
В)′  А′
А′  В′ доказано.
В′ доказано.
Докажем второе включение. Так как А  (А
(А  В), то А′
В), то А′ 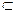 (А
(А  В)′. Из В
В)′. Из В 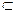 (А
(А  В) следует В′
В) следует В′ 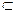 (А
(А  В)′, тогда имеем: А′
В)′, тогда имеем: А′  В′
В′ 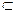 (А
(А  В)′.
В)′.
б) Рассуждения аналогичны пункту а).
в) Пусть х  А′\В′. Тогда х – предельная точка А, но не является предельной точкой В. Из последнего следует, что в любой окрестности S(x; δ) существует x1 ¹ x, х1
А′\В′. Тогда х – предельная точка А, но не является предельной точкой В. Из последнего следует, что в любой окрестности S(x; δ) существует x1 ¹ x, х1  А и х1
А и х1 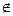 В, т.е. х1
В, т.е. х1  А \ В. Таким образом, х есть предельная точка множества А \ В, т.е. х
А \ В. Таким образом, х есть предельная точка множества А \ В, т.е. х  (А \ В)′. Включение доказано.
(А \ В)′. Включение доказано.
г) Так как А′ замкнуто (см. задачу №46), то А′′ = (А′)′ 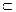 А′.
А′.
50. а) 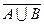 = (А
= (А  В)
В)  (А′
(А′  В′) = (А
В′) = (А  А′)
А′)  (В
(В  В′) =
В′) =  .
.
б) 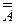 =
= 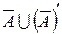 , из задачи №48(а) имеем
, из задачи №48(а) имеем 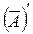
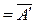 , тогда
, тогда 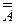 =
= 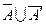 = (А
= (А  А′)
А′)  (А′
(А′  А′′) (так как
А′′) (так как 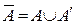 ). Так как А′′
). Так как А′′ 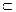 А′ (см. задачу №48(г)), то А′
А′ (см. задачу №48(г)), то А′  А′′ = А′, тогда
А′′ = А′, тогда 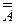 = (
= ( )
)  =
=  =
=  . Следовательно,
. Следовательно, 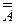 =
= 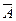 .
.
г) 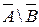 = (А
= (А  А′) \ (В
А′) \ (В  В′) = (А \ В)
В′) = (А \ В)  (А′ \ В′). Из задачи № 48(в) имеем А′ \ В′
(А′ \ В′). Из задачи № 48(в) имеем А′ \ В′ 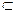 (А \ В)′, тогда
(А \ В)′, тогда 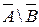
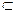 (А \ В)
(А \ В)  (А \ В)′ =
(А \ В)′ = 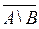 .
.
д) Так как А 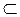 В, то А′
В, то А′ 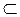 В′, но тогда
В′, но тогда 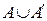
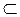 В
В  В′, т.е.
В′, т.е. 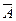
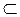
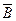 .
.
е) 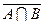 =
= 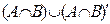 . Так как
. Так как 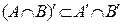 (см. задачу №48(б)), то
(см. задачу №48(б)), то 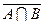
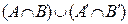 =
= 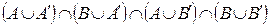
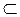
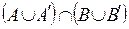 = =
= = 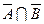 . Таким образом,
. Таким образом, 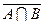
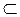
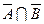 .
.
51. Из задачи №50(е) имеем 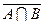
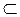
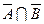 . С другой стороны,
. С другой стороны, 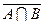
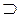
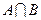 . По условию, А =
. По условию, А = 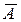 , В =
, В = 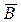 , тогда
, тогда 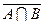
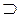
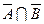 . В итоге получаем доказываемое равенство.
. В итоге получаем доказываемое равенство.
52. а) Пусть х  Int(E), тогда х – внутренняя точка Е, т.е. существует окрестность S(x; δ) такая, что S(x; δ) ∩ Е = S(x; δ), но Е
Int(E), тогда х – внутренняя точка Е, т.е. существует окрестность S(x; δ) такая, что S(x; δ) ∩ Е = S(x; δ), но Е 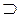 S(x; δ) ∩ Е, следовательно, х
S(x; δ) ∩ Е, следовательно, х  Е. Таким образом, в силу произвольности точки х, имеет место включение Int(E)
Е. Таким образом, в силу произвольности точки х, имеет место включение Int(E) 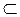 Е.
Е.
б) Включение Int(Int(E))  Int(E) следует из предыдущего пункта. Докажем «обратное» включение. Пусть х
Int(E) следует из предыдущего пункта. Докажем «обратное» включение. Пусть х  Int(E). Так как x – произвольная точка, то Int(E) – открытое множество, т.е. все его точки принадлежат внутренности. Тогда х
Int(E). Так как x – произвольная точка, то Int(E) – открытое множество, т.е. все его точки принадлежат внутренности. Тогда х  Int(Int(E)). Откуда имеем Int(E)
Int(Int(E)). Откуда имеем Int(E)  Int(Int(E)). Следовательно, Int(Int(E)) = Int(E).
Int(Int(E)). Следовательно, Int(Int(E)) = Int(E).
в) Пусть х0  Int(E1
Int(E1 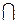 Е2), тогда х0 – внутренняя точка множества E1
Е2), тогда х0 – внутренняя точка множества E1 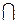 Е2, т.е. существует S(x0; δ) такая, что S(x0; δ)
Е2, т.е. существует S(x0; δ) такая, что S(x0; δ)  (E1
(E1  Е2) = S(x0; δ). Преобразуем левую часть равенства, получим (S(x0; δ)
Е2) = S(x0; δ). Преобразуем левую часть равенства, получим (S(x0; δ)  E1)
E1)  (S(x0; δ)
(S(x0; δ)  E2)=S(x0; δ). Тогда х0 – внутренняя точка Е1 и внутренняя точка Е 2, т.е. х0
E2)=S(x0; δ). Тогда х0 – внутренняя точка Е1 и внутренняя точка Е 2, т.е. х0  Int(E1)
Int(E1)  Int (Е2). Отсюда имеем включение Int(E1
Int (Е2). Отсюда имеем включение Int(E1  Е2)
Е2)  Int(E1)
Int(E1)  Int (Е2).
Int (Е2).
Пусть х0  Int(E1)
Int(E1)  Int (Е2), тогда х0 одновременно есть внутренняя точка Е1 и Е2, т.е. существует S(x0; δ1) такая, что S(x0; δ1)
Int (Е2), тогда х0 одновременно есть внутренняя точка Е1 и Е2, т.е. существует S(x0; δ1) такая, что S(x0; δ1)  Е1 = S(x0; δ1), и существует S(x0; δ2) такая, что S(x0; δ2)
Е1 = S(x0; δ1), и существует S(x0; δ2) такая, что S(x0; δ2)  Е2 = S(x0; δ2). Выберем min(δ1, δ2)=δ, тогда S(x0; δ)
Е2 = S(x0; δ2). Выберем min(δ1, δ2)=δ, тогда S(x0; δ)  (E1
(E1  Е2) = S(x0; δ), т.е. х0
Е2) = S(x0; δ), т.е. х0  Int(E1
Int(E1  Е2). Значит имеет место Int(E1)
Е2). Значит имеет место Int(E1)  Int (Е2)
Int (Е2)  Int(E1
Int(E1  Е2), что в итоге дает доказываемое равенство.
Е2), что в итоге дает доказываемое равенство.
г) Пусть х0  Int(E1). Тогда существует окрестность S(x0; δ), такая, что
Int(E1). Тогда существует окрестность S(x0; δ), такая, что
S(x0; δ)  Е1 = S(x0; δ). Так как Е1
Е1 = S(x0; δ). Так как Е1  Е2, то S(x0; δ)
Е2, то S(x0; δ) 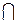 Е1
Е1 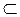 S(x0; δ)
S(x0; δ) 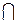 Е2. Следовательно, х0
Е2. Следовательно, х0  Int(E2). Таким образом, так как х0 – любая, Int(E1)
Int(E2). Таким образом, так как х0 – любая, Int(E1) 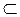 Int(E2).
Int(E2).
53.  Множество решений неравенства f(x)
Множество решений неравенства f(x) 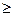 а есть подмножество замкнутого множества Е, т.е. множество тех точек из Е, для которых выполняется неравенство f(x)
а есть подмножество замкнутого множества Е, т.е. множество тех точек из Е, для которых выполняется неравенство f(x) 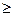 а. Так как Е замкнуто, то Е содержит все свои предельные точки. Пусть { xn } последовательность таких точек из Е, что f(xn)
а. Так как Е замкнуто, то Е содержит все свои предельные точки. Пусть { xn } последовательность таких точек из Е, что f(xn) 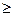 а. Покажем, что если
а. Покажем, что если 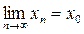 (х0 – предельная; х0
(х0 – предельная; х0  Е в силу его замкнутости), то х0
Е в силу его замкнутости), то х0  Е(f(x)
Е(f(x) 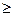 а). Так как функция f(x) непрерывна, то
а). Так как функция f(x) непрерывна, то 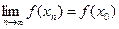 . С другой стороны, для любого n f(xn)
. С другой стороны, для любого n f(xn) 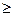 а. При предельном переходе получим, что и f(x0)
а. При предельном переходе получим, что и f(x0) 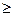 а, т.е. х0
а, т.е. х0  Е(f(x)
Е(f(x) 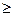 а). Следовательно, множество Е(f(x)
а). Следовательно, множество Е(f(x) 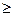 а) – замкнуто.
а) – замкнуто.
58. а) 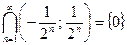 не является открытым.
не является открытым.
б) 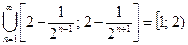 не является замкнутым.
не является замкнутым.
59. Пусть G – открытое множество. Тогда CG – замкнуто. Рассмотрим два случая:
1). Если CG = ø, то G = (– ∞; +∞). Тогда G = 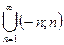 , где n
, где n  N. Множество интервалов {(– n;n)} счетно, следовательно, G представлено в виде счетной совокупности интервалов с рациональными концами.
N. Множество интервалов {(– n;n)} счетно, следовательно, G представлено в виде счетной совокупности интервалов с рациональными концами.
2). Если CG ≠ ø, то G ≠ (– ∞; +∞). Так как G – открытое множество, то все его точки внутренние, т.е. для любого х  G существует интервал (rx; rx′), где rx,rx′ – рациональные числа, целиком содержащийся в G. Множество интервалов вида (rx; rx′) счетно, тогда G =
G существует интервал (rx; rx′), где rx,rx′ – рациональные числа, целиком содержащийся в G. Множество интервалов вида (rx; rx′) счетно, тогда G = 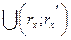 есть объединение счетной совокупности интервалов с рациональными концами.
есть объединение счетной совокупности интервалов с рациональными концами.
60. Так как открытое множество G – ограничено, то каждая его точка принадлежит некоторому составляющему интервалу, т.е. такому, что при aк  G, bк
G, bк  G (aк;bк)
G (aк;bк) 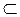 G. Причем составляющие интервалы либо тождественны, либо не пересекаются. Множество составляющих интервалов не более чем счетно, так как оно эквивалентно подмножеству рациональных чисел. Тогда G =
G. Причем составляющие интервалы либо тождественны, либо не пересекаются. Множество составляющих интервалов не более чем счетно, так как оно эквивалентно подмножеству рациональных чисел. Тогда G = 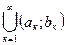 .
.
61. Из предыдущей задачи G = 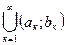 , где (aк;bк) – составляющие интервалы. Представим любой интервал (aк;bк)в виде суммы
, где (aк;bк) – составляющие интервалы. Представим любой интервал (aк;bк)в виде суммы 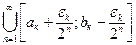 , где
, где 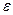 k <
k < 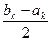 . Таким образом, любой интервал представлен в виде счетной совокупности отрезков. Тогда множество G тоже может быть представлено в виде счетной совокупности отрезков: G =
. Таким образом, любой интервал представлен в виде счетной совокупности отрезков. Тогда множество G тоже может быть представлено в виде счетной совокупности отрезков: G = 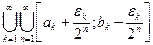 .
.
62. Предположим, что числовая прямая представлена в виде счетной совокупности попарно непересекающихся отрезков, т.е. (– ∞; +∞) = 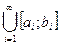 , где [ ai;bi ]
, где [ ai;bi ] 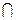 [ aj;bj ] = ø при i
[ aj;bj ] = ø при i 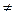 j. Рассмотрим множество Q =
j. Рассмотрим множество Q = 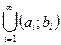 . Q – открыто. Множество CQ = E – совершенно, так как получено из числовой прямой путем удаления взаимно непересекающихся интервалов, не имеющих общих концов. Мощность множества Е равна с.
. Q – открыто. Множество CQ = E – совершенно, так как получено из числовой прямой путем удаления взаимно непересекающихся интервалов, не имеющих общих концов. Мощность множества Е равна с.
Рассмотрим множество М = С(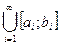 ). По допущению, оно пусто. Но, с другой стороны, М = E \ {a1;b1;a2;b2;…}. Тогда
). По допущению, оно пусто. Но, с другой стороны, М = E \ {a1;b1;a2;b2;…}. Тогда  = с – а = с, т.е. не пусто. Получили противоречие. Следовательно, R нельзя представить в виде счетной совокупности попарно непересекающихся отрезков.
= с – а = с, т.е. не пусто. Получили противоречие. Следовательно, R нельзя представить в виде счетной совокупности попарно непересекающихся отрезков.
63. Нет, так как любой интервал (а;b) ~ (– ∞; +∞), а в предыдущей задаче было показано, что (– ∞; +∞) нельзя представить в виде объединения взаимно непересекающихся отрезков.
64. Пусть [ a;b ] =  , тогда среди всех отрезков найдутся два таких, что ai = a; bk = b. Множество [ a;b ] \ ([ ai;bi ]
, тогда среди всех отрезков найдутся два таких, что ai = a; bk = b. Множество [ a;b ] \ ([ ai;bi ]  [ ak;bk ]) = (bi;ak) – интервал. В задаче №63 показано, что его нельзя представить в виде счетной совокупности взаимно непересекающихся отрезков.
[ ak;bk ]) = (bi;ak) – интервал. В задаче №63 показано, что его нельзя представить в виде счетной совокупности взаимно непересекающихся отрезков.
66. Множество E  – замкнуто. Покажем, что оно не содержит изолированных точек. Тогда по задаче №65 оно совершенно.
– замкнуто. Покажем, что оно не содержит изолированных точек. Тогда по задаче №65 оно совершенно.
Пусть х0  E
E  . Так как а
. Так как а 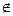 Е и b
Е и b 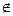 Е, то х0 – внутренняя точка отрезка [ a;b ]. Тогда существует точка х, принадлежащая окрестности точки х0, причем окрестность S(x0; δ)
Е, то х0 – внутренняя точка отрезка [ a;b ]. Тогда существует точка х, принадлежащая окрестности точки х0, причем окрестность S(x0; δ) 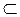 [ a; b ]. Значит, точка х0 не является изолированной точкой множества E
[ a; b ]. Значит, точка х0 не является изолированной точкой множества E 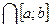 . Отсюда, в силу произвольности точки х0 ,
. Отсюда, в силу произвольности точки х0 ,
заключаем: E 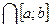 – совершенное множество.
– совершенное множество.
67. а) Каждую точку множества Р0 можно представить в виде троичной дроби 0,а1а2а3…, где ak равно либо 0, либо 2.
Концы интервалов являются точками «первого рода» и представлены следующим образом: либо, начиная с некоторого места троичное разложение имеет все двойки, т.е. имеется бесконечная троичная дробь (например, 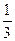 = 0,0222…,
= 0,0222…,  = 0,0022…), либо все нули, т.е. возникает конечная троичная дробь (например,
= 0,0022…), либо все нули, т.е. возникает конечная троичная дробь (например, 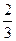 = 0,2000…,
= 0,2000…, 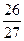 =
= 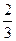 +
+ 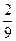 +
+ 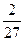 = 0,222000…). Все остальные точки являются точками «второго рода». В троичном разложении они имеют бесконечно много нулей и двоек (так,
= 0,222000…). Все остальные точки являются точками «второго рода». В троичном разложении они имеют бесконечно много нулей и двоек (так, 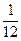 = 0,0020202…=
= 0,0020202…= 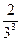 +
+ 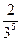 +
+ 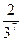 +…).
+…).
б) Между 0,1 и 0,2 находится точка  . Эта точка – конец интервала, ее троичное разложение таково: 0,00222….
. Эта точка – конец интервала, ее троичное разложение таково: 0,00222….
в) Между 0,05 и 0,1 или между 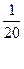 и
и 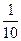 находится точка
находится точка 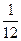 , ее троичным разложением будет 0,0020202… Она не является концом интервала, т.е. это – точка «второго рода».
, ее троичным разложением будет 0,0020202… Она не является концом интервала, т.е. это – точка «второго рода».
г) Множество точек «первого рода» канторова множества Р0 эквивалентно бесконечному подмножеству множества рациональных чисел. Следовательно, его мощность равна а.
д) Мощность множества точек «второго рода» Р0 равна: с – а = с.
70. а) Множеству Р0 принадлежит 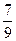 , не принадлежат Р0:
, не принадлежат Р0: 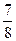 ;
; 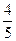 ;
; 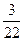 .
.
72. Назовем отрезок [0; 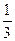 ] и отрезок [
] и отрезок [ 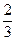 ; 1], оставшиеся после исключения интервала (
; 1], оставшиеся после исключения интервала (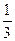 ;
; 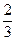 ), отрезками первого ранга; отрезки [0;
), отрезками первого ранга; отрезки [0; 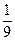 ], [
], [ 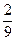 ;
;  ],
],
[ 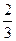 ;
;  ], [
], [ 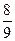 ;1], оставшиеся после исключения интервалов (
;1], оставшиеся после исключения интервалов (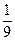 ;
; 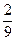 ), (
), (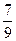 ;
; 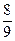 ) – отрезками второго ранга и т.д. Отрезки n -го ранга имеют длину
) – отрезками второго ранга и т.д. Отрезки n -го ранга имеют длину 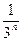 . Чтобы получить из отрезка n -го ранга отрезок (n+1)-го ранга, нужно исключить из него интервалы длины
. Чтобы получить из отрезка n -го ранга отрезок (n+1)-го ранга, нужно исключить из него интервалы длины 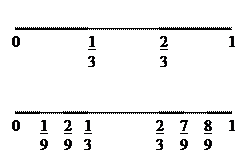
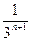 с центром в середине отрезка (см. рис. 3).
с центром в середине отрезка (см. рис. 3).


Рис. 3
Докажем, что любой интервал (α; β) содержит в себе интервал, полностью свободный от точек Р0. Если произвольный интервал (α; β) не содержит точек Р0, то Р0 нигде не плотно. Если (α; β) содержит какой-нибудь отрезок n -го ранга, то можно выбрать интервал длиной 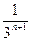 с центром в середине этого сегмента. Этот интервал не содержит точек из Р0 и вместе с тем содержится в интервале (α; β). Значит, Р0 нигде не плотно на прямой.
с центром в середине этого сегмента. Этот интервал не содержит точек из Р0 и вместе с тем содержится в интервале (α; β). Значит, Р0 нигде не плотно на прямой.
78. Пусть множество Е состоит из n точек. Покроем каждую точку интервалом длины 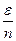 , где ε – сколь угодно мало. Получим покрытие множества Е протяженностью ε. Следовательно, m *E = 0, тогда и m *E = 0, так как m *E
, где ε – сколь угодно мало. Получим покрытие множества Е протяженностью ε. Следовательно, m *E = 0, тогда и m *E = 0, так как m *E 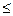 m *E и m *E
m *E и m *E 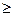 0. Итак, m Е = 0.
0. Итак, m Е = 0.
79. Покроем точки счетного множества Е интервалами длины  ,
, 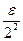 , …,
, …, 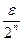 , …. Суммарная длина этих интервалов будет равна
, …. Суммарная длина этих интервалов будет равна  = ε
= ε 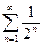 = ε. Следовательно, m *E = 0 и m *E = 0. Тогда m Е = 0.
= ε. Следовательно, m *E = 0 и m *E = 0. Тогда m Е = 0.
80. Множество иррациональных точек отрезка [ a;b ] есть дополнение множества рациональных точек из [ a;b ]. Так как множество рациональных точек отрезка счетно, то его мера равна нулю. Отсюда мера множества иррациональных чисел отрезка [ a;b ] равна (b – a) – 0 = b – a.
82. А = (0; 1); В = [0; 1].
88. m Pα = α; m Gα = 1 – α.
89. Множество нулевой меры измеримо; всякое его подмножество, в том числе и подмножество типа Е(f > A), также измеримо и имеет меру нуль.
90. Представим множество Е(f 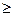 A) в виде
A) в виде
Е(f 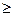 A) =
A) = 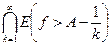 ,
,
Тогда оно будет измеримо как пересечение счетного множества измеримых множеств. Далее, из равенств
Е(f 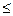 A) = Е \ Е(f > A), Е(f < A) = E \ Е(f
A) = Е \ Е(f > A), Е(f < A) = E \ Е(f 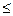 A)
A)
следует, что каждое из множеств Е(f 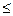 A) и Е(f < A) измеримо, как разность двух измеримых множеств.
A) и Е(f < A) измеримо, как разность двух измеримых множеств.
91. Зададим произвольное А. Могут возникнуть два случая (см. рис. 4):
а) А 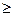 с, тогда Е(f > A) = ø измеримо;
с, тогда Е(f > A) = ø измеримо;
б) А< c, тогда Е(f > A) = Е измеримо, по условию.

Рис. 4
92. Возможны случаи:
а) 0 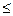 А < 1, тогда Е(f > A) есть множество рациональных точек отрезка, оно измеримо;
А < 1, тогда Е(f > A) есть множество рациональных точек отрезка, оно измеримо;
б) А 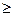 1, Е(f > A) = ø;
1, Е(f > A) = ø;
в) А < 0, Е(f > A) = [ a;b ].
93. Указание. Рассмотреть: а) А 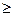 f(b); б) А < f(a); в) f(a)
f(b); б) А < f(a); в) f(a) 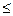 A < f(b).
A < f(b).
94. Если А < 0, то Е(f > A) = [0; 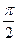 ] измеримо;
] измеримо;
если А 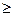 1, то Е(f > A) = ø;
1, то Е(f > A) = ø;
если 0 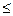 А < 1, тогда Е(f > A) есть множество всех рациональных точек отрезка [0;
А < 1, тогда Е(f > A) есть множество всех рациональных точек отрезка [0; 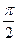 ] или его подмножество, они измеримы.
] или его подмножество, они измеримы.
95. Множество Е(f 3 > A) измеримо по условию. Но Е(f 3 > A) =
= Е(f > 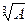 ), следовательно, и множество Е(f >
), следовательно, и множество Е(f > 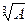 ) измеримо. Таким образом, множество Е(f >
) измеримо. Таким образом, множество Е(f > 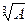 ) измеримо для произвольного
) измеримо для произвольного 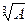 , т.е. f(x) – измеримая функция на Е.
, т.е. f(x) – измеримая функция на Е.
96. Рассмотрим, например, на E = [ a,b ] функцию:
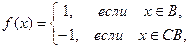 где B – неизмеримо(
где B – неизмеримо(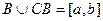 ).
).
f(x) – неизмеримая функция, так как неизмеримо множество 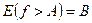 при
при  , а функция
, а функция 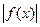 = 1 измерима.
= 1 измерима.
97. Достаточно показать, что для любого действительного числа А множество Е(f 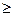 A) замкнуто, а следовательно, измеримо. Рассмотрим множество Е(f < A). Оно будет открытым, так как каждая его точка является внутренней (это следует из непрерывности f(x)). Тогда Е(f
A) замкнуто, а следовательно, измеримо. Рассмотрим множество Е(f < A). Оно будет открытым, так как каждая его точка является внутренней (это следует из непрерывности f(x)). Тогда Е(f 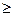 A) замкнуто, как дополнение открытого множества Е(f < A).
A) замкнуто, как дополнение открытого множества Е(f < A).
105. Множество Е(f > A) измеримо для любого А, так как его можно представить в виде суммы измеримых множеств Е i (f > A).
108. Функция Дирихле φ(х) – неинтегрируемая по Риману на [0; 1], так как она разрывна в каждой точке этого отрезка.
(L) 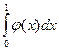 = (L)
= (L) 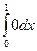 = 0,
= 0,
так как функции у = φ(х) и у = 0 эквивалентны на [0; 1] (их значения различны на множестве меры нуль).
109. 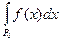 = 0, так как mP0 = 0.
= 0, так как mP0 = 0.
110. Разобьем отрезок [0; 5] на оси ОУ на 5 частей точками:
у0 = 0, у1 = 1, у2 = 2, у3 = 3, у4 = 4, у5 = 5 (см. рис. 5).

Рис. 5
Составим интегральную сумму Лебега:
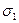 =
=  = 0·1+1·1 +2·1+3·1+4·1 = 10.
= 0·1+1·1 +2·1+3·1+4·1 = 10.
Рассмотрим новое разбиение отрезка [0; 5]:
у0 = 0, у1 = 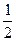 , у2 = 1, у3 =
, у2 = 1, у3 = 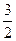 , у4 = 2, …, у9=
, у4 = 2, …, у9= 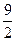 , у10 = 5.
, у10 = 5.
Найдем 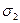 = 0·1+
= 0·1+ 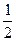 ·0 + 1·1 +
·0 + 1·1 + 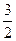 ·0 +2·1 +
·0 +2·1 + 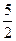 ·0+3·1 +
·0+3·1 + 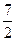 ·0+4·1 +
·0+4·1 + 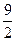 ·0= 10.
·0= 10.
Продолжая вычислять суммы Лебега для различных разбиений, получим последовательность: 10, 10, …, 10, …, предел которой при 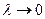 есть интеграл Лебега от функции f(x) на отрезке [0; 5] и он равен 10. Интеграл Римана совпадает с площадью ступенчатой фигуры и также равен 10.
есть интеграл Лебега от функции f(x) на отрезке [0; 5] и он равен 10. Интеграл Римана совпадает с площадью ступенчатой фигуры и также равен 10.
111. Функции y = f(x)[1 – φ(х)] и y = f(x) отличаются друг от друга только на множестве рациональных чисел, мера которого равна 0, поэтому
(L) 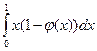 = (L)
= (L) 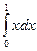 = (R)
= (R) 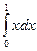
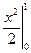 =
= 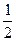 .
.
112. а) Функция g(x) = cos2x на [0; 1] отличается от данной функции
y = f(x) лишь на множестве Р0 меры 0. Следовательно,
(L) 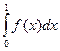 = (L)
= (L) 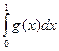 .
.
Последний интеграл совпадает с интегралом Римана, так как y = g(x) непрерывна на [0; 1] и, следовательно, по Риману интегрируема.
б) (L) 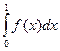 = (L)
= (L) 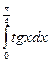 + (L)
+ (L)  .
.
Интегралы в правой части равны соответствующим интегралам Римана, так как подынтегральные функции непрерывны.
113. а) y = f(x) не интегрируема по Риману, так как разрывна в каждой точке отрезка [0; 1]. По Лебегу онаинтегрируема, так как ограничена и измерима на [0; 1].
(L) 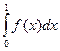 = (L)
= (L) 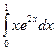 = (R)
= (R) 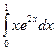 .
.
б) Указание. Решить аналогично №113(а).
114. Указание. Решить аналогично №112(б).
115. а) (L) 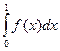 = (L)
= (L) 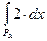 + (L)
+ (L) 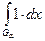 = 2 ·mPα + 1· mGα = 1 + α.
= 2 ·mPα + 1· mGα = 1 + α.
б) (L) 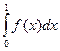 = (L)
= (L) 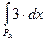 + (L)
+ (L) 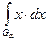 = 3 α +
= 3 α + 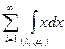 = 3 α +
= 3 α + 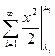 ,
,
где (λi, μi) – составляющие интервалы множества Gα, т.е. Gα = 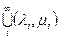 .
.
116. а) Нет. Не выполнена аксиома тождества: из равенства 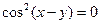 не следует, что x = y.
не следует, что x = y.
б) Да. Выполнение аксиомы треугольника следует из неравенства 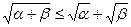 , которое справедливо при любых α ≥ 0, β ≥ 0 (проверяется это неравенство извлечением квадратного корня из обеих частей очевидного неравенства
, которое справедливо при любых α ≥ 0, β ≥ 0 (проверяется это неравенство извлечением квадратного корня из обеих частей очевидного неравенства 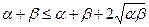 ).
).
117. Да.
118. Вначале необходимо убедиться, что для любых последовательностей x = (x1, x2, …, xn, …) и y = (y1, y2, …, yn, …), у которых ряд из модулей членов этих последовательностей сходится, расстояние ρ(x, y) будет определено. Действительно, ряд 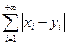 сходится, так как
сходится, так как 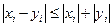 , а ряды
, а ряды 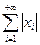 и
и 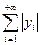 сходятся (по условию).
сходятся (по условию).
119. Если ряды  и
и 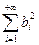 сходятся, то и ряд
сходятся, то и ряд 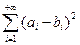 сходится. Это следует из того, что (ai – bi)2 = ai2 – 2 aibi + bi2 ≤ ai2 + (ai2 + bi2) + bi2 =
сходится. Это следует из того, что (ai – bi)2 = ai2 – 2 aibi + bi2 ≤ ai2 + (ai2 + bi2) + bi2 =
= 2(ai2 + bi2).
Выполнение первых двух аксиом метрического пространства очевидно. Для проверки третьей аксиомы воспользуемся неравенством, справедливым для n -мерного евклидова пространства:
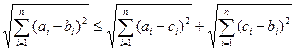 .
.
Переходя в этом неравенстве к пределу при n → ∞, получаем
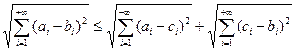 .
.
120. Выполнение первых двух аксиом метрического пространства очевидно. Проверим выполнение аксиомы треугольника. Для любых ограниченных функций x(t), y(t), z(t) на отрезке [ a, b ] имеем:
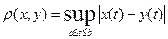 ≤
≤ 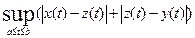 ≤
≤
≤ 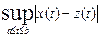 +
+ 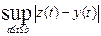 =
= 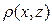 +
+ 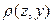 .
.
121. Аксиома треугольника проверяется интегрированием (на отрезке [ a,b ]) неравенства 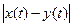 ≤
≤ 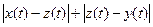 .
.
122. а) Неравенство можно получить предельным переходом при  из неравенства Коши-Буняковского, записанного для конечных сумм
из неравенства Коши-Буняковского, записанного для конечных сумм
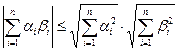 , (3)
, (3)
если принять 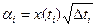 ,
, 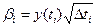 .
.
б) Умножив в неравенстве (3) обе части на 2, а затем прибавив к обеим частям выражение 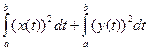 , после преобразований получим
, после преобразований получим
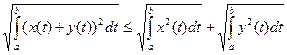 . (4)
. (4)
123. Выполнение первых двух аксиом метрического пространства очевидно. Проверим выполнение аксиомы треугольника. Пусть u(t), v(t), w(t) – произвольные непрерывные функции на отрезке [ a, b ]. Подставляя в неравенство (4) x(t) = u(t) – v(t), y(t) = v(t) – w(t), получим: 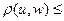
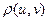 +
+ 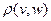 , т.е. аксиома треугольника выполнена.
, т.е. аксиома треугольника выполнена.
125. 1) Пусть { xn (xn  , xn
, xn  , …, xn
, …, xn 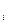 , …)} – фундаментальная последовательность элементов пространства l1. По определению, для любого ε > 0 найдется номер N такой, что при любых n > N, m > N имеет место неравенство
, …)} – фундаментальная последовательность элементов пространства l1. По определению, для любого ε > 0 найдется номер N такой, что при любых n > N, m > N имеет место неравенство
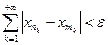 . (5)
. (5)
Из неравенства 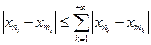 следует, что числовая последовательность
следует, что числовая последовательность 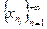 при любом i – фундаментальная и, значит, сходится.
при любом i – фундаментальная и, значит, сходится.
Пусть ai = 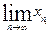 . Покажем, что a (a1, a2, …, an, …)
. Покажем, что a (a1, a2, …, an, …)  l1 и xn → a в l1.
l1 и xn → a в l1.
Действительно, из нераве
Date: 2015-09-24; view: 1125; Нарушение авторских прав