Тема 11. Гильбертовы пространства и обобщенные ряды Фурье

1. Понятие гильбертова пространства.

2. Ортогональные системы векторов в гильбертовом пространстве.

3. Критерий полноты ортогональной системы.

4. Ряды Фурье в гильбертовых пространствах.

См. список литературы: [1, гл. 1, 2].

Краткие теоретические сведения

Вещественное линейное пространство называется евклидовым, если каждой паре его элементов 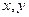поставлено в соответствие вещественное число, обозначаемое 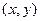и называемое скалярным произведением так, что выполняются следующие аксиомы:

1) 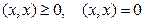тогда и только тогда, когда х ≡ 0;

2) ;

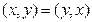3) 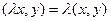для любого ;

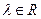4) .

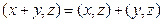Множество Н называется нормированным пространством, если каждому элементу х пространства Н ставится в соответствие действительное число, называемое нормой этого элемента и обозначаемое 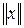, которое удовлетворяет следующим условиям (аксиомам нормы):

1) ;

2) ;

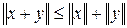3) , .

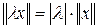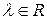Из неравенства Коши – Буняковского 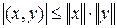вытекает, что в евклидовом пространстве можно ввести норму элемента х равенством: .

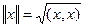Последовательность элементов { х_n } линейного нормированного пространства сходится к х, если 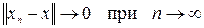. Определенная таким образом сходимость называется сходимостью по норме.

Последовательность { х_n } нормированного пространства называется фундаментальной, если при 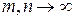, т.е. .

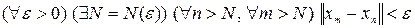Лемма: Всякая сходящаяся в нормированном пространстве последовательность является фундаментальной.

Нормированное пространство называется полным (или пространство называется полным в норме), если в нем сходится всякая фундаментальная последовательность.

Бесконечномерное пространство Н со скалярным произведением называется гильбертовым, если оно является полным по метрике или полным в этой норме 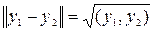. Например, евклидово пространство является гильбертовым.

Углом между ненулевыми элементами 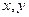вещественного гильбертова пространства называется угол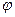 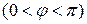такой, что 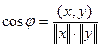. Элементы 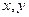называют ортогональными, если .

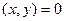Система ненулевых элементов 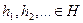называется ортогональной, есл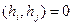и при .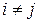

Ортогональная система 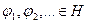называется полной, если любой элемент х из Н может быть представлен в виде так называемого ряда Фурь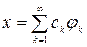е: , где 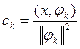– коэффициенты Фурье ().

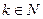Задачи

137. Проверить, что следующие векторные пространства являются гильбертовыми:

1) 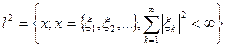со скалярным произведением 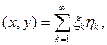где ;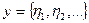

2) со скалярным произведением .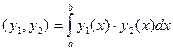

138. В линейном пространстве 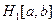непрерывно дифференцируемых на отрезке 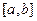функций положим 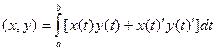. Является ли данное пространство гильбертовым?

139. Доказать существование ортонормального базиса в любом гильбертовом пространстве.

140. Пусть 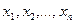– ортогональная система в гильбертовом пространстве Н, 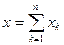. Доказать, что .

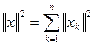141. Установить, что размерность 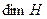гильбертова пространства 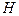не зависит от выбора ортонормального базиса.

142. Проверить, что изоморфизм гильбертовых пространств Н и Н ₁ имеет место тогда и только тогда, когда .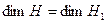

Date: 2015-09-24; view: 848; Нарушение авторских прав