Тема 7. Интеграл Лебега от ограниченной измеримой функции

1. Определение и существование интеграла Лебега от ограниченной измеримой функции.

2. Основные свойства интеграла Лебега.

3. Вычисление интеграла Лебега.

4. Сравнение интегралов Римана и Лебега.

5. Критерий интегрируемости по Риману ограниченной функции.

См. список литературы: [4, гл. 6.4]; [5, гл. 5.1 – 5.4].

Краткие теоретические сведения

1. Интеграл Римана. При определении интеграла Римана от ограниченной на отрезке [ a; b ] функции f(x), этот отрезок разбивается на части точками

a = x₀ < x₁ < … < x_i < x_i+1 < … < x_n = b.

На каждом участке [ x_i; x_i+1 ] произвольно выбирается точка ξ_i и составляется интегральная сумма:

σ = .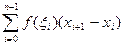

Если при λ → 0, где λ = 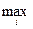(x_i+1 – x_i), существует конечный предел интегральной суммы σ, не зависящий ни от способа дробления отрезка [ a; b ], ни от выбора точек ξ_i, то этот предел называется интегралом Римана от функции f(x) и обозначается (R) 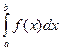или .

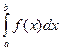Теорема. Для того чтобы функция f(x) была интегрируема по Риману, необходимо и достаточно, чтобы она была ограничена на [ a; b ] и мера Лебега множества точек ее разрыва равнялась нулю, т.е. чтобы f(x) была почти всюду непрерывна на [ a; b ].

2. Интеграл Лебега. Пусть f: E → [A; B] – ограниченная, измеримая функция, Е – измеримое множество. В отличие от предыдущего разбивается на части не множество Е, расположенное на оси абсцисс, а принадлежащий оси ординат отрезок [A; B], включающий все значения функции f(x):

А = у₀ < y₁ < y₂< … < у_i < у_i+1 < … < у_n = В.

Далее рассматриваются множества e_i = E(y_i ≤ f(x) < y_i+1) и составляется интегральная сумма σ = .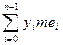

Если существует конечный предел суммы σ при λ → 0, где

λ = 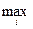(у_i+1 – у_i), то этот предел называется интегралом Лебега от функции f(x) и обозначается (L) 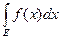или .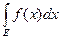

Если Е = [ a; b ], то пишут (L) 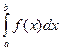(или ).

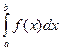Теорема. Всякая ограниченная, измеримая на Е функция интегрируема по Лебегу на этом множестве.

3. Свойства интеграла Лебега.

а) Если А ≤ f(x) ≤ B, то А× mЕ ≤ (L) 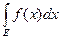≤ B× mE.

б) Если множество Е = 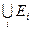, где E_i – попарно непересекающиеся измеримые множества, то (L) 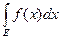= 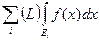(полная аддитивность интеграла Лебега).

в) Если две функции f(x) и g(x) равны почти всюду на множестве Е, т.е. mE(f 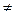g) = 0, то 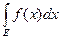(L) = (L) .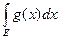

4. Связь интегралов Римана и Лебега.

Если функция f(x) интегрируема по Риману на отрезке [ a; b ], то на нем она интегрируема по Лебегу и (L) 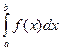= (R) .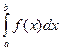

Задачи

107. Доказать, что всякая функция с ограниченным изменением (см. задачу № 102) интегрируема по Риману на [ a; b ].

108. Доказать, что функция Дирихле не интегрируема по Риману на отрезке [0; 1]. Проинтегрировать ее по Лебегу на этом отрезке.

109. Доказать, что (L) 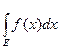= 0, если mE = 0. Найти (L) 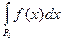, где Р₀ – множество Кантора.

110. Cоставьте интегральные суммы Лебега для функции f(x) = [ x ], проведя все подсчеты для отрезка [0; 5]. Убедитесь в том, что предел их сумм при λ → 0 совпадает с (R) .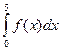

111. Доказать, что 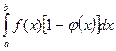(L) = (L) 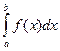, где φ(x) – функция Дирихле, f(x) – интегрируемая по Лебегу функция. Найти (L) .

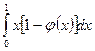112. Найти интеграл Лебега на отрезке [0; 1] от следующих функций:

a) f(x) =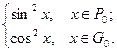

б) f(x) =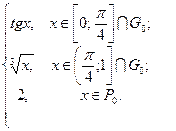

113. Будут ли интегрируемы по Риману на отрезке [0; 1] следующие функции:

а) f(x) =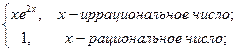

б) f(x) =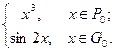

Интегрируемы ли они по Лебегу на [0; 1]? Если да, вычислите соответствующий интеграл Лебега.

114. Найти интеграл Лебега на [0; π] от функции

f(x) =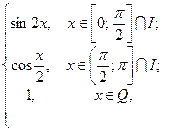

где I – множество иррациональных, Q – множество рациональных точек отрезка [0; π].

115. Показать, что следующие функции не интегрируемы по Риману на [0; 1] и не эквивалентны никакой функции, интегрируемой по Риману:

а) f(x) =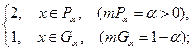

б) f(x) =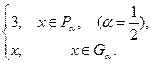

Найти интеграл Лебега от каждой из этих функций на отрезке [0; 1].