
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

V. Элементы функционального анализа
|
|
Тема 8. Метрические пространства. Основные понятия
1. Понятие метрического пространства.
2. Примеры метрических пространств.
3. Окрестности точек в метрическом пространстве. Классификация точек и множеств в метрическом пространстве.
4. Определения и свойства открытых и замкнутых множеств точек метрического пространства.
См. список литературы: [1, гл. 3.1 –3.4]; [4, гл. 7.1 –7.2].
Краткие теоретические сведения
1. Метрическим пространством называется произвольное множество М элементов, называемых точками, в котором для любой пары элементов 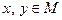 определено число
определено число  , называемое расстоянием от х до у (или метрикой), обладающее следующими свойствами:
, называемое расстоянием от х до у (или метрикой), обладающее следующими свойствами:
а) для любых 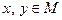
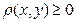 , причем
, причем 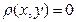 тогда и только тогда, когда х = у (аксиома тождества);
тогда и только тогда, когда х = у (аксиома тождества);
б) для любых 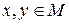
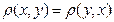 (аксиома симметрии);
(аксиома симметрии);
в) для любых 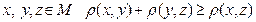 (аксиома треугольника).
(аксиома треугольника).
2. Примеры метрических пространств.
Евклидовы пространства 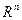 : множество упорядоченных групп из n элементов действительных чисел
: множество упорядоченных групп из n элементов действительных чисел 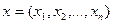 , где
, где 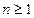 с расстоянием
с расстоянием 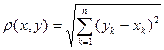 . В частности, при n= 1
. В частности, при n= 1 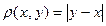 возникает пространство
возникает пространство 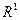 (множество действительных чисел R).
(множество действительных чисел R).
Гильбертово пространство 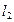 . Множество числовых последовательностей
. Множество числовых последовательностей 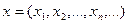 , для которых
, для которых 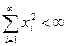 (т.е. ряд сходится). Метрика:
(т.е. ряд сходится). Метрика: 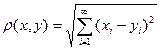 .
.
Пространство непрерывных на  функций
функций 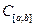 . Элементы – непрерывные функции
. Элементы – непрерывные функции 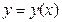 на
на  ;
; 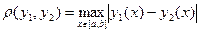 .
.
3. Определение шара в метрическом пространстве. Шаром 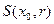 метрического пространства М с центром в точке
метрического пространства М с центром в точке 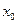 и радиусом
и радиусом 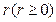 называется множество точек
называется множество точек 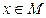 , удовлетворяющих неравенству
, удовлетворяющих неравенству 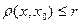 .
.
Задачи
116. Будет ли множество R действительных чисел метрическим пространством, если расстояние между элементами х и у определить формулами:
а) 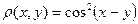 ; б)
; б)  ?
?
117. Будет ли множество точек плоскости хОу метрическим пространством, если расстояние между точками 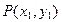 и
и 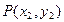 определить формулой
определить формулой 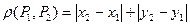 ?
?
118. Доказать, что множество последовательностей 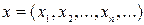 , удовлетворяющих условию
, удовлетворяющих условию 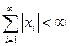 , образует метрическое пространство, если расстояние между элементами
, образует метрическое пространство, если расстояние между элементами 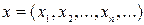 и
и 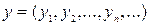 определить формулой
определить формулой 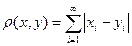 . Что представляет собою в этом пространстве шар
. Что представляет собою в этом пространстве шар 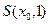 , где
, где 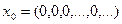 ? Привести примеры элементов, принадлежащих этому шару.
? Привести примеры элементов, принадлежащих этому шару.
119. Используя неравенства Коши-Буняковского: 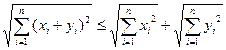 ;
; 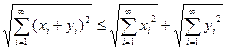 , показать, что
, показать, что 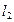 и
и 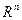 являются метрическими пространствами.
являются метрическими пространствами.
120. Доказать, что множество М всех ограниченных (не обязательно непрерывных) на отрезке  функций
функций 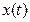 образует метрическое пространство, если расстояние между элементами
образует метрическое пространство, если расстояние между элементами 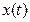 и
и 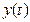 определить формулой
определить формулой 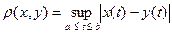 .
.
121. Доказать, что множество непрерывных на отрезке  функций
функций 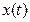 образует метрическое пространство С 1, если расстояние между элементами
образует метрическое пространство С 1, если расстояние между элементами 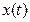 и
и 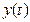 определить формулой
определить формулой 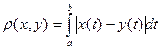 .
.
122. Доказать неравенства Коши-Буняковского для интегралов: а) 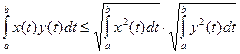 ; б)
; б) 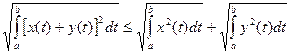 .
.
123. Доказать, что множество непрерывных на отрезке  функций
функций 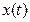 образует метрическое пространство С 2, если расстояние между элементами
образует метрическое пространство С 2, если расстояние между элементами 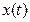 и
и 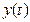 определить формулой
определить формулой 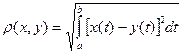 .
.
Date: 2015-09-24; view: 873; Нарушение авторских прав