
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 3. Замкнутые и открытые множества
|
|
1. Понятие предельной точки. Примеры.
2. Замкнутые множества. Их свойства. Примеры.
3. Открытые множества. Их свойства. Примеры.
4. Совершенные множества.
См. список литературы: [4, гл. 2.4 – 2.8]; [5, гл. 2.1 – 2.3].
Краткие теоретические сведения
Пусть x, y  E. Неотрицательная функция
E. Неотрицательная функция 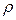 (х, у), ставящая в соответствие любой паре элементов х, у множества Е некоторое неотрицательное действительное числои удовлетворяющая трем аксиомам:
(х, у), ставящая в соответствие любой паре элементов х, у множества Е некоторое неотрицательное действительное числои удовлетворяющая трем аксиомам:
1. (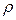 (х, у) = 0)
(х, у) = 0) 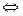 (х = у) – аксиома тождества;
(х = у) – аксиома тождества;
2. 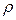 (х, у) =
(х, у) = 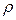 (у, х) – аксиома симметрии;
(у, х) – аксиома симметрии;
3. 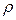 (х, у)
(х, у) 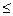
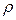 (х, z) +
(х, z) + 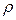 (z, у) – аксиома треугольника,
(z, у) – аксиома треугольника,
называется расстоянием между элементами х и у (или метрикой множества Е). Множество, на котором определена метрика, называется метрическим пространством.
Далее рассматриваются только линейные множества, т.е. множества точек числовой прямой R. Метрика этого пространства:
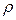 (х, у) =
(х, у) = 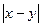 .
.
Окрестностью 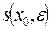 точки х0 называется множество всех точек х метрического пространства, удовлетворяющих условию:
точки х0 называется множество всех точек х метрического пространства, удовлетворяющих условию: 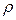 (х, х0) <
(х, х0) < 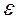 . Число
. Число 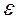 > 0 называется радиусом окрестности.
> 0 называется радиусом окрестности.
Пусть Е 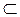 R. Точка х0
R. Точка х0  R называется предельной точкой множества Е, если в любой окрестности точки х0 содержится хотя бы одна точка х
R называется предельной точкой множества Е, если в любой окрестности точки х0 содержится хотя бы одна точка х  Е, отличная от х0.
Е, отличная от х0.
Из определения следует, что в любой окрестности предельной точки содержится бесконечное множество точек из Е.
Множество всех предельных точек множества Е называется производным множеством и обозначается Е .
Множество 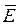 = Е
= Е  Е называется замыканием множества Е.
Е называется замыканием множества Е.
Если Е 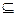 Е, то множество Е называется замкнутым.
Е, то множество Е называется замкнутым.
Если Е 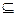 Е , то множество Е называется плотным в себе.
Е , то множество Е называется плотным в себе.
Если Е = Е , то Е называется совершенным множеством.
Точка х0 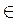 Е называется изолированный точкой множества Е, если существует окрестность
Е называется изолированный точкой множества Е, если существует окрестность 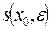 , не содержащая ни одной отличной от х0 точки множества Е, т.е.:
, не содержащая ни одной отличной от х0 точки множества Е, т.е.:
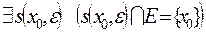 .
.
Точка х0 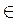 Е называется внутренней точкой множества Е, если существует окрестность
Е называется внутренней точкой множества Е, если существует окрестность 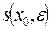 точки х0, такая что
точки х0, такая что
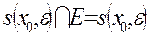 .
.
Множество всех внутренних точек множества Е называется внутренностью множества Е и обозначается Int(E).
Множество, все точки которого внутренние, называется открытым.
Задачи
41. Найти предельные точки множеств:
а) {1, 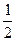 ,
, 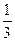 , …,
, …, 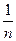 , …};
, …};
б) A = 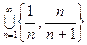 ;
;
в) A = 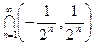 ;
;
г) A = (0; 2)  (-1; 1);
(-1; 1);
д) A = [0;2) 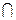 (-1; 0].
(-1; 0].
42. Пусть Е – производное множество множества Е. Доказать, что а 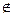 Е тогда и только тогда, когда существует окрестность S точки а такая, что
Е тогда и только тогда, когда существует окрестность S точки а такая, что 
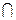 E – бесконечное множество.
E – бесконечное множество.
43. Доказать, что конечное множество не имеет предельных точек.
44. Доказать, что а  Е \ Е тогда и только тогда, когда существует такая окрестность
Е \ Е тогда и только тогда, когда существует такая окрестность 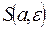 , что Е
, что Е 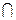 S = { a }.
S = { a }.
45. Пусть Е – некоторое множество точек, расстояние между которыми 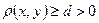 . Доказать, что Е не имеет предельных точек.
. Доказать, что Е не имеет предельных точек.
46. Доказать, что производное множество Е любого бесконечного множества Е замкнуто.
47. Докажите эквивалентность следующих условий:
а) Е – замкнуто;
б) Е = 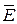 .
.
48. Докажите, что
а) (А  В) = А
В) = А  В ;
В ;
б) (А 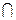 В) = А
В) = А 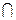 В ;
В ;
в) А \ В 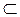 (А \ В) ;
(А \ В) ;
г) А 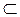 А .
А .
49. Заполните следующую таблицу:
| Множество | Является ли множество | Найти | ||||||
| ограни-ченным | замкну-тым | откры-тым | совер-шенным | 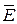
| Int(E) | Е | Е\ Е¢ | |
| Ø | ||||||||
| R | ||||||||
| Q | ||||||||
| I | ||||||||
| конечное | ||||||||
| (a; b) | ||||||||
| (a; b] | ||||||||
| [a; b) | ||||||||
| [a; b] | ||||||||
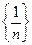
| ||||||||
{1;0}  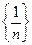
|
50. Пусть 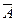 – замыкание множества А. Доказать, что:
– замыкание множества А. Доказать, что:
а) 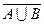 =
=  ;
;
б) 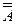 =
= 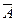 ;
;
в) А 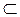
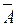 ;
;
г) 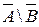
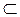
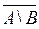 ;
;
д) (А 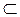 В)
В) 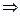 (
(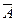
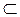
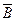 );
);
е) 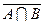
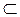
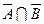 .
.
51. Доказать, что если А = 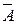 и В =
и В = 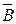 , то
, то 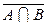 =
= 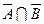 .
.
52. Пусть Int(E) – внутренность множества Е. Доказать, что:
а) Int(E) 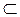 Е;
Е;
б) Int(Int(E)) = Int(E);
в) Int(E1 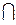 Е2) = Int(E1)
Е2) = Int(E1) 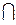 Int(Е2);
Int(Е2);
г) (Е1 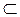 Е2)
Е2) 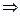 (Int(E1)
(Int(E1) 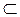 Int(Е2)).
Int(Е2)).
53. Пусть f(x) – непрерывна на замкнутом множестве. Доказать, что множество решений неравенства f(x) 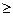 a – замкнуто.
a – замкнуто.
54. Пусть Gi (i = 1, 2, …, n) – открытые множества. Доказать, что:
а) 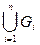 – открыто;
– открыто;
б) 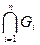 – открыто.
– открыто.
55. Доказать, что сумма любого числа открытых множеств открыта.
56. Пусть F i (i = 1, 2, …, n) – замкнутые множества. Доказать, что:
а) 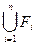 – замкнуто;
– замкнуто;
б) 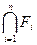 – замкнуто.
– замкнуто.
57. Доказать, что пересечение любого числа замкнутых множеств замкнуто.
58. Привести примеры:
а) счетного множества открытых множеств, пересечение которых не является открытым множеством;
б) счетного множества замкнутых множеств, объединение которых не является замкнутым множеством.
Date: 2015-09-24; view: 1283; Нарушение авторских прав