Тема 4. Строение линейных множеств

1. Структура линейных открытых множеств.

2. Структура линейных замкнутых множеств.

3. Канторово совершенное множество и его свойства.

4. Мощность совершенного множества.

См. список литературы: [4, гл. 2.6 – 2.10]; [5, гл. 2.5 – 2.6].

Краткие теоретические сведения

Разделив на три части точкам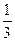и и 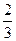отрезок [0; 1], удалим из него интервал (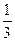; 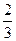). Разделив каждый из двух оставшихся отрезков на три части, удалим средние интервалы: (; 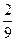) и (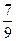; 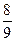). Далее делим на три равные части оставшиеся четыре отрезка и удалим из них средние интервалы (рис. 1). Продолжим процесс неограниченно.

Рис. 1

В результате из отрезка [0; 1] удалим открытое множество

G₀ = .

При этом останется множество P₀ = [0; 1] \ G₀, являющееся совершенным.

Множества P₀ и G₀ – называются множествами Кантора.

Задачи

59. Доказать, что любое открытое множество можно представить в виде суммы счетного множества интервалов с рациональными концами.

60. Доказать, что открытое ограниченное множество можно представить в виде суммы не более чем счетного множества попарно непересекающихся интервалов.

61. Доказать, что каждое открытое непустое ограниченное множество можно представить в виде суммы счетного множества отрезков.

62. Доказать, что прямую нельзя представить в виде суммы счетной совокупности попарно непересекающихся отрезков.

63. Можно ли представить интервал (a; b) в виде суммы счетного множества попарно непересекающихся отрезков?

64. Можно ли представить отрезок [ a; b ] в виде суммы счетной совокупности попарно непересекающихся отрезков?

65. Доказать, что замкнутое множество Е совершенно тогда и только тогда, когда в нем нет изолированных точек.

66. На прямой даны отрезок [ a; b ] и совершенное множество Е, причем концы отрезка не принадлежат Е. Доказать, что множество Е 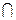[ a; b ] является совершенным.

67. Точки совершенного канторова множества Р₀ подразделяются на точки «первого рода», являющиеся концами смежных интервалов, и точки «второго рода», не являющиеся концами смежных интервалов.

а) Какова арифметическая структура точек «первого» и «второго» рода канторова множества Р₀?

б) Найти какую-либо точку «первого рода» множества Р₀, заключенную между числами 0,1 и 0,2.

в) Найти какую-либо точку «второго рода» множества Р₀, заключенную между числами 0,05 и 0,1.

г) Определить мощность множества точек «первого рода» множества Р_0.

д) Определить мощность множества точек «второго рода» множества Р_0.

е) Найти замыкание множества точек «первого рода» и замыкание множества точек «второго рода» множества Р₀.

68. Пусть G₀ – канторово множество и а [0; 1]. Показать, что а G₀ тогда и только тогда, когда а невозможно разложить в троичную дробь без помощи единицы.

69. Пусть Р₀ – канторово совершенное множество и а [0; 1]. Показать, что а Р₀ тогда и только тогда, когда а можно разложить в троичную дробь без помощи единицы.

70. а) Какие из чисел 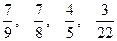принадлежат множеству Р₀?

б) Показать, что Int(P₀) = Ø.

в) Показать, что 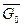= [0; 1].

71. Множество Е называется плотным на множестве А, если замыкание 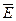включает А, т.е.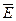 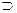А. Показать, что G₀ плотно на [0; 1].

72. Множество Е называется нигде не плотным на прямой, если между любыми двумя числами из Е лежит промежуток чисел, не входящих в Е. Доказать, что множество Р₀ нигде не плотно на прямой.

73. На прямой даны интервал (α; β) и совершенное, нигде не плотное множество Е. Доказать, что их пересечение является либо совершенным множеством, либо счетной совокупностью попарно непересекающихся совершенных множеств.

74. На прямой даны два совершенных, нигде не плотных множества P и Q. Доказать, что разность этих множеств P \ Q является либо совершенным множеством, либо суммой счетного множества попарно непересекающихся совершенных множеств.

75. Канторовы множества P_α и G_α.

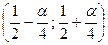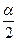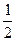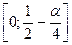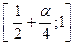Пусть α – произвольное положительное число из интервала (0; 1). Удалим из отрезка [0; 1] интервал длины с центром в точке . Из оставшихся отрезков и удалим средние интервалы длины 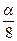. Процесс продолжим неограниченно. В результате из отрезка удалим открытое множество G_α, останется совершенное множество P_α. Множества P_α и G_α также называются множествами Кантора.

а) Доказать, что Int(P_α) = Ø;

б) Показать, что 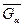= [0; 1].

Date: 2015-09-24; view: 1179; Нарушение авторских прав