
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нахождение параметров уравнения линейной регрессии по методу наименьших квадратов
|
|
(стр. 291- 298)
Пусть коэффициент корреляции между двумя случайными величинами значимо отличается от нуля и близок к единице. Предполагаем (выдвигаем гипотезу), что эти случайные величины связаны «в среднем» линейной зависимостью:
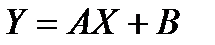
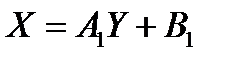
РЕГРЕССИЯ – оптимальная зависимость, то есть модель, обеспечивающая аппроксимацию эмпирических данных с наибольшей точностью. Справедливо соотношение

Коэффициенты 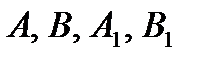 являются параметрами линейной регрессионной модели. Величина
являются параметрами линейной регрессионной модели. Величина 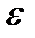 - случайная ошибка наблюдений, причем математическое ожидание
- случайная ошибка наблюдений, причем математическое ожидание 
Для нахождения оценок параметров модели используем метод наименьших квадратов. Согласно этому методу в качестве оценок параметров выбирают такие, которые обеспечивают минимум суммы квадратов отклонений наблюдаемых значений случайных величин от их математических ожиданий. Другими словами параметры должны быть такими, чтобы сумма
 принимала наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных
принимала наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных 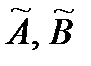 , приравнивая к нулю частные производные
, приравнивая к нулю частные производные
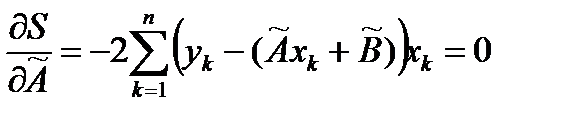

В результате для нахождения оценок получаем систему уравнений:
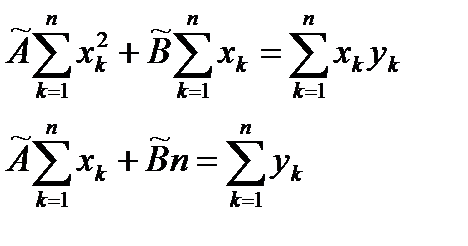
Решение системы имеет вид:
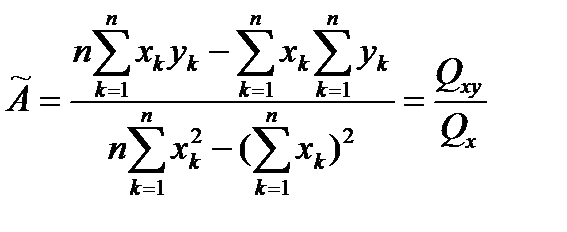 ,
, 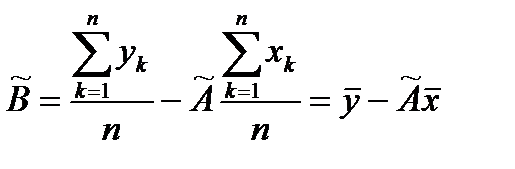 .
.
Аналогично находим оценки
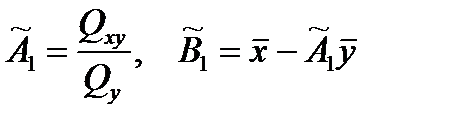 . При этом
. При этом 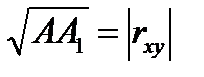 .
.
Для рассмотренной задачи
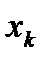
| 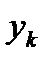
|
| 0,9 | 6,1 |
| 1,7 | 12,3 |
| 2,3 | 11,5 |
| 4,6 | 15,9 |
| 5,3 | 14,1 |

имеем оценки
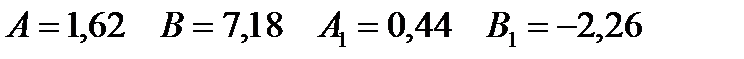
И уравнения регрессии имеют вид 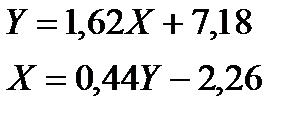
Достаточно легко написать программу для получения оценок по методу наименьших квадратов как для линейной, так и для других зависимостей. Но существует много готовых программных средств, решающих эту задачу. Так средства EXCEL позволяют непосредственно получить уравнение линейной регрессии по рядам данных:
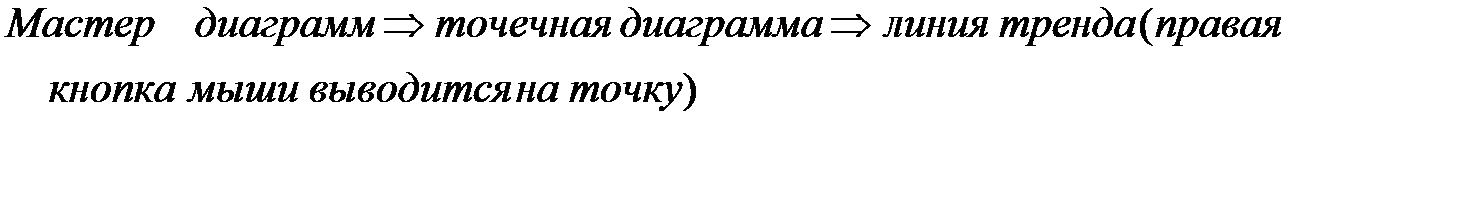
Регрессионная модель называется адекватной, если предсказанные по ней значения переменной 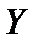 согласуются с результатами наблюдений. Оценка адекватности может быть проведена следующим образом.
согласуются с результатами наблюдений. Оценка адекватности может быть проведена следующим образом.
Непосредственный анализ остатков, то есть разностей между наблюдаемыми значениями 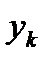 и вычисленными согласно уравнению регрессии
и вычисленными согласно уравнению регрессии 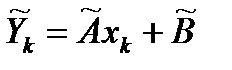 :
:
.
Если модель адекватна, то остатки, которые являются реализациями случайных ошибок наблюдений, должны быть нормально распределенными случайными величинами с нулевым средним и одинаковыми дисперсиями 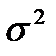 . Другими словами для случайной величины - остатков – необходимо выполнить лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное отклонение) и доказать, что на заданном уровне значимости
. Другими словами для случайной величины - остатков – необходимо выполнить лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное отклонение) и доказать, что на заданном уровне значимости 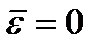 (нулевое значение
(нулевое значение  попадает в доверительный интервал для математического ожидания).
попадает в доверительный интервал для математического ожидания).
Пример построения прямой регрессии в Excel.


Данные описательной статистики для случайной величины “остатки”
| Среднее | 6,66134E-16 |
| Стандартная ошибка | 0,108822029 |
| Медиана | 0,109108445 |
| Мода | |
| Стандартное отклонение | 0,486666907 |
| Дисперсия выборки | 0,236844679 |
| Эксцесс | 0,294111648 |
| Асимметричность | -0,602186657 |
| Интервал | 1,892506228 |
| Минимум | -1,181791019 |
| Максимум | 0,710715209 |
| Сумма | 1,33227E-14 |
| Счет | |
| Уровень надежности(95,0%) | 0,227767194 |
Из приведенных зависимостей и расчетов видно, что предложенная регрессионная модель адекватна: остатки распределены около нулевого среднего. Значение стандартной ошибки  задает доверительный интервал для
задает доверительный интервал для 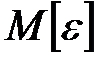 , содержащий значение
, содержащий значение 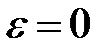 .
.
Статистическую значимость регрессионной модели можно проверить по коэффициенту регрессиии 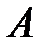 .
.
Линейная регрессионная модель называется незначимой, если параметр 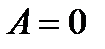 . Проверку основной гипотезы
. Проверку основной гипотезы  против альтернативной гипотезы
против альтернативной гипотезы 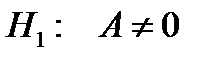 можно провести двумя способами.
можно провести двумя способами.
СПОСОБ 2. Находим границы доверительного интервала для параметра 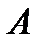 :
:
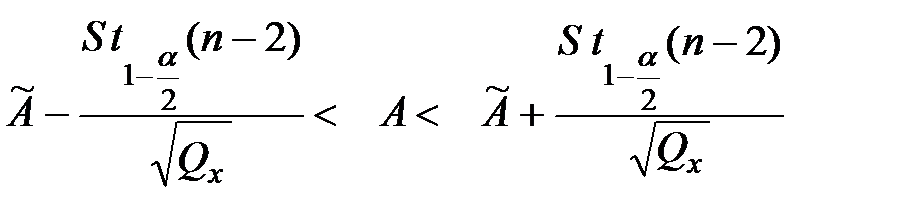
Если для данного уровня значимости доверительный интервал содержит значение 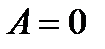 , то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимой
, то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимой
Например: 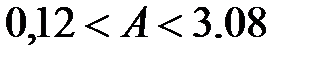 или
или  .
.
Таким образом, на заданном уровне значимости нулевое значение параметра не попадает в доверительный интервал и регрессия признается статистически значимой
Полезной и важной характеристикой линейной регрессии является коэффициент детерминации 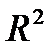 , который вычисляют по формуле
, который вычисляют по формуле
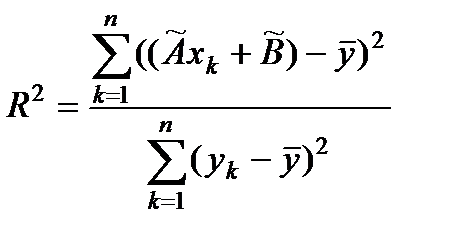 .
.
Этот коэффициент показывает долю разброса результатов наблюдений около средего значения случайной величины  , которую можно объяснить построенной регрессионной моделью, и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов
, которую можно объяснить построенной регрессионной моделью, и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов 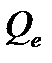 , тем ближе значение коэффициента к единице и тем точнее выбранная модель регрессии описывает результаты наблюдений. Значение корня
, тем ближе значение коэффициента к единице и тем точнее выбранная модель регрессии описывает результаты наблюдений. Значение корня 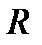 является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае линейной регресссии справедливо
является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае линейной регресссии справедливо 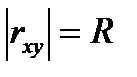 . Отметим, что именно значение коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации.
. Отметим, что именно значение коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации.
Ниже приведена выдача из Excel:  , для подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента регрессии
, для подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента регрессии 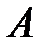 :
: 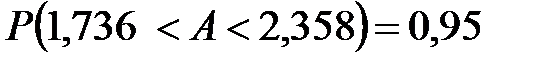 .
.
| ВЫВОД ИТОГОВ | ||||||||||||||||
| Регрессионная статистика | ||||||||||||||||
| Множественный R | 0,956037 | |||||||||||||||
| R-квадрат | 0,914006 | |||||||||||||||
| Нормированный R-квадрат | 0,909229 | |||||||||||||||
| Стандартная ошибка | 0,500003 | |||||||||||||||
| Наблюдения | ||||||||||||||||
| Дисперсионный анализ | ||||||||||||||||
| df | SS | MS | F | Значимость F | ||||||||||||
| Регрессия | 47,83 | 47,83 | 191,3179 | 4,96562E-11 | ||||||||||||
| Остаток | 4,500049 | 0,250003 | ||||||||||||||
| Итого | 52,33004 | |||||||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |||||||||||
| Y-пересечение | -0,43605 | 0,718975 | -0,60648 | 0,5517664 | -1,946557679 | 1,074464255 | ||||||||||
| Переменная X 1 | 2,047796 | 0,14805 | 13,83177 | 4,966E-11 | 1,736753836 | 2,358837984 | ||||||||||
Date: 2015-09-24; view: 639; Нарушение авторских прав