
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вторая теорема разложения
|
|
Пусть изображение Лапласа 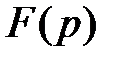 является правильной дробью:
является правильной дробью:
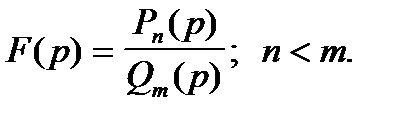
Тогда оригиналом является функция 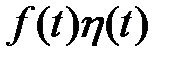 , где
, где

Сумма вычетов берется по всем особым точкам, лежащим в конечной части комплексной плоскости.
Если изображение 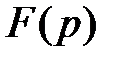 является неправильной дробью, то необходимо выделить целую часть и при нахождении оригинала использовать свойство линейности.
является неправильной дробью, то необходимо выделить целую часть и при нахождении оригинала использовать свойство линейности.
Пример 2. 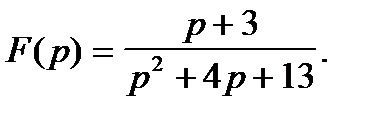
Так как дробь правильная, сразу находим особые точки: 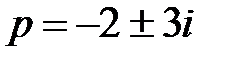 , которые являются простыми полюсами. Сумму вычетов в комплексно сопряженных точках удобно находить по формуле:
, которые являются простыми полюсами. Сумму вычетов в комплексно сопряженных точках удобно находить по формуле:
 |
| 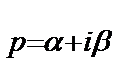 +
+ 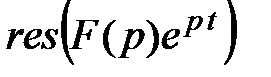 |
|  =
= 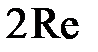
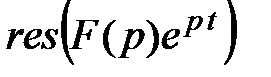 |
| 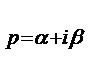 .
.
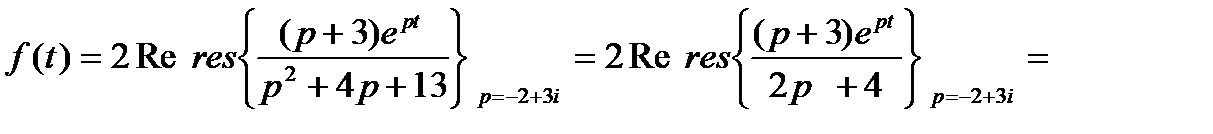
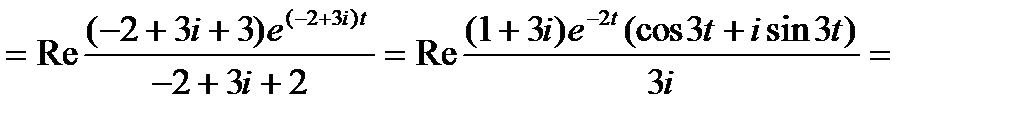
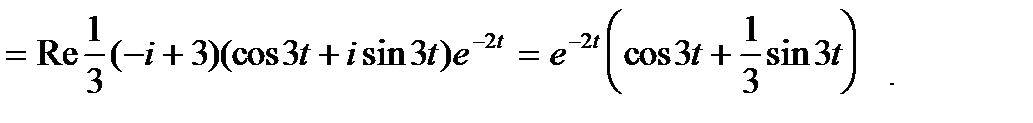
Пример 3. 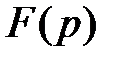 =
= 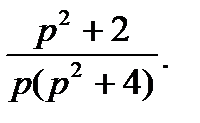
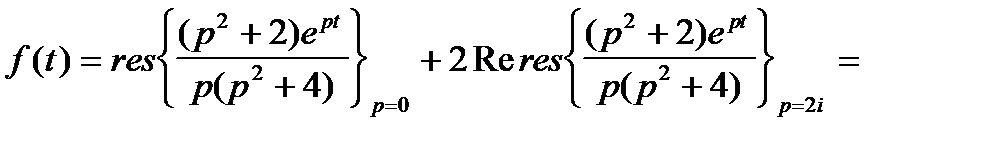
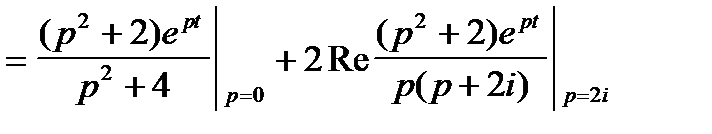
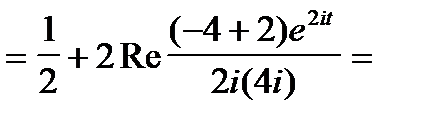
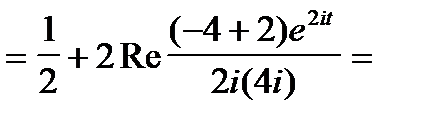
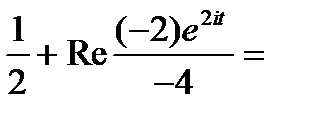
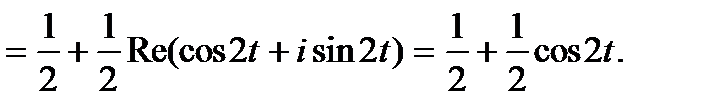
Пример 4. 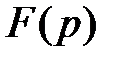 =
= 
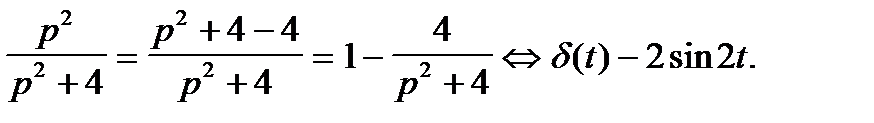
ТАБЛИЦА: ОСНОВНЫЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА И ИХ СВОЙСТВА
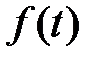
| 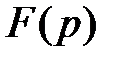
| 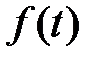
| 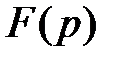
|
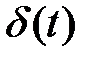
| 
| 
| |

| 
|  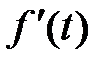
| 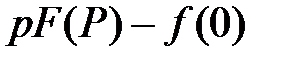
|

| 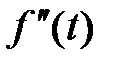
| 
| |
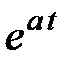
| 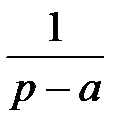
| 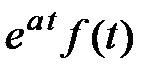
| 
|

| 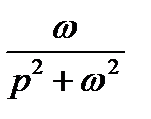
|
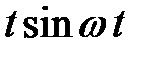
| 
|
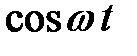
| 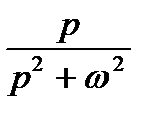
|
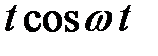
| 
|
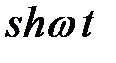
| 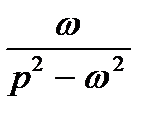
| 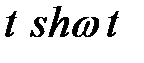
| 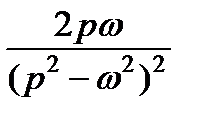
|
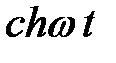
| 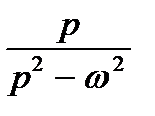
|

| 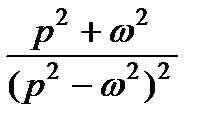
|

| 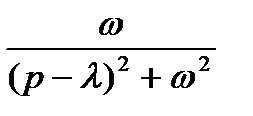
| 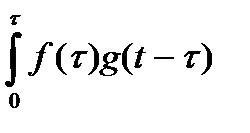
| 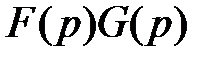
|
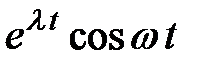
| 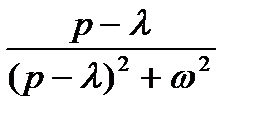
| 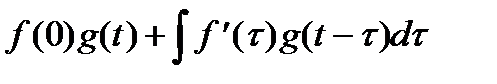
| 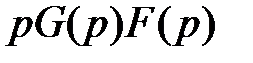
|
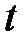
| 
| 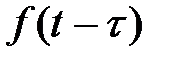
| 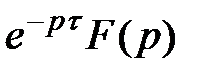
|

| 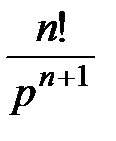
|
ЗАДАЧИ
1. Найдите изображение 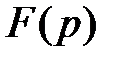 по оригиналу
по оригиналу 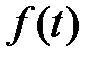 , используя определение преобразований Лапласа.
, используя определение преобразований Лапласа.
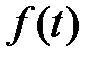
|

|
| τ |
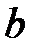
|
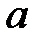
|
| t |
| T |
Ответы:
1. 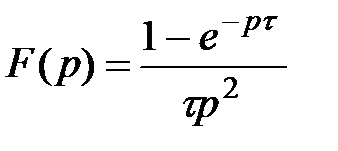 ,
,
2. 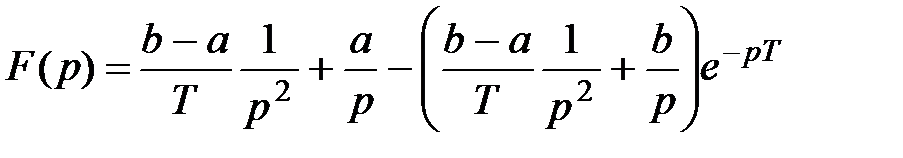
2. Найдите изображение по оригиналу, используя таблицу и свойства преобразований Лапласа.
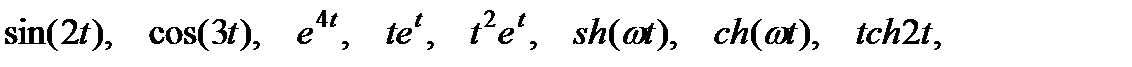
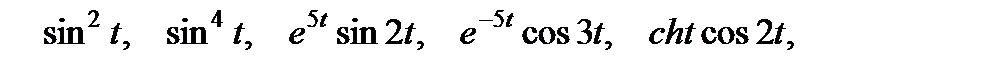

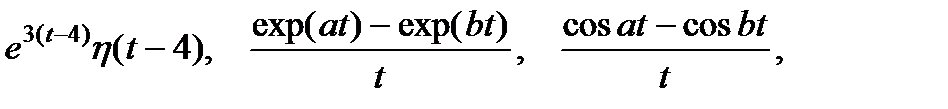
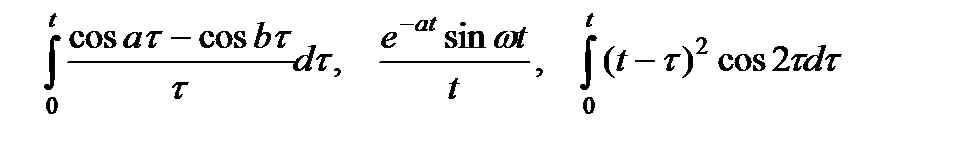
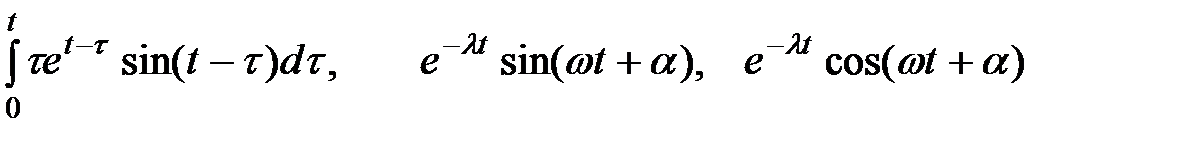
4. Преобразования Лапласа: восстановите оригинал по изображению
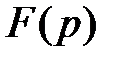
| Ответ: 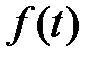
| |
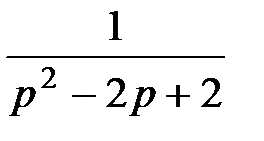
| 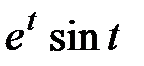
| |
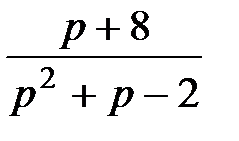
| 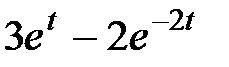
| |
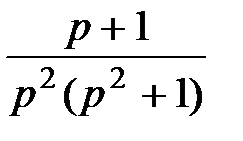
| 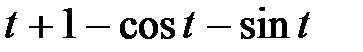
| |
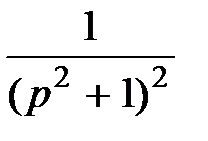
| 
| |
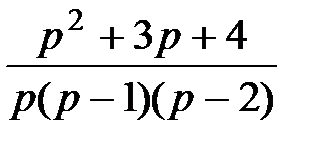
| 
| |

|  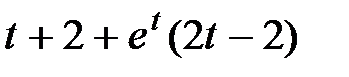
| |

| 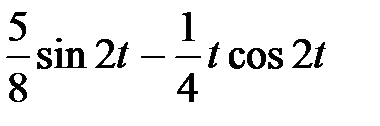
| |

| 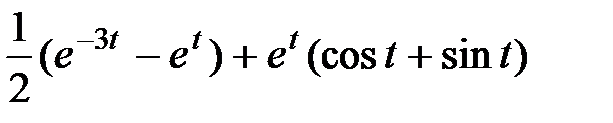
| |
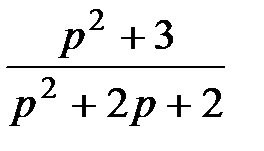
| 
| |
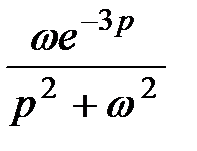
| 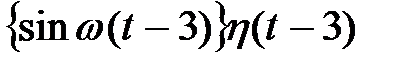
| |
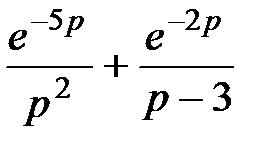
| 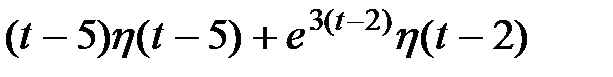
| |

| 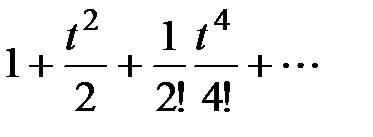
| |
6. Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом
Задача Коши для линейного уравнения:
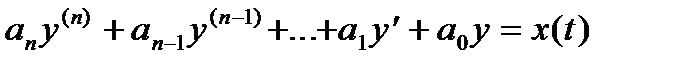
состоит в нахождении частного решения y(t) по заданным начальным условиям
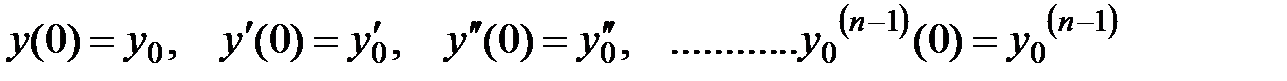
Полагаем, что правая часть уравнения x(t) и искомая функция y(t) являются оригиналами. Тогда для них существует преобразование Лапласа:
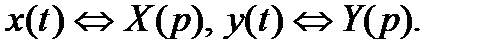
Применяя правило дифференцирования оригинала

................................
и используя свойство линейности, переходим в исходном дифференциальном уравнении от оригиналов к изображениям. При этом исходное дифференциальное уравнение переходит в алгебраическое уравнение относительно  :
:

Тогда
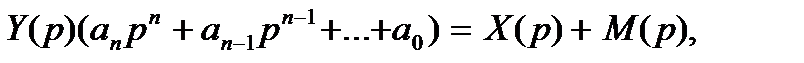
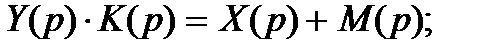
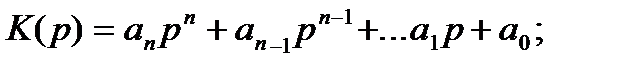
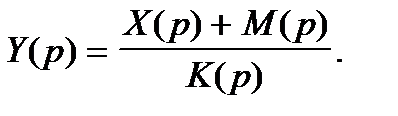
B этом выражении стоящий в знаменателе многочлен 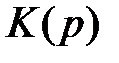 называется характеристическим многочленом, а функция
называется характеристическим многочленом, а функция 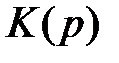 выражает влияние начальных условий.
выражает влияние начальных условий.
Решение исходного дифференциального уравнения получаем, возвращаясь к оригиналам 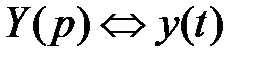 .
.
Пример 5. Найти частное решение уравнения
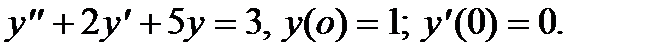
Переходя к изображениям 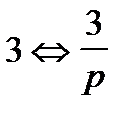 ,
, 
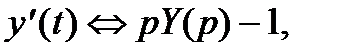
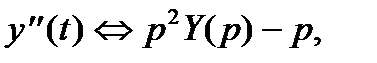
получаем операторное уравнение
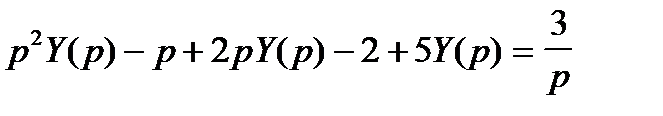
и его решение
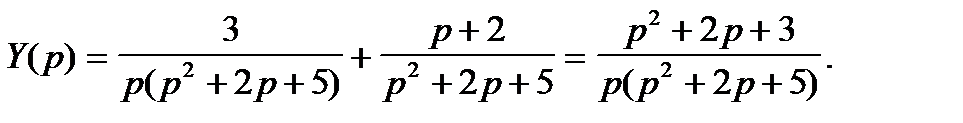
Переходя к оригиналам, получаем искомое решение:
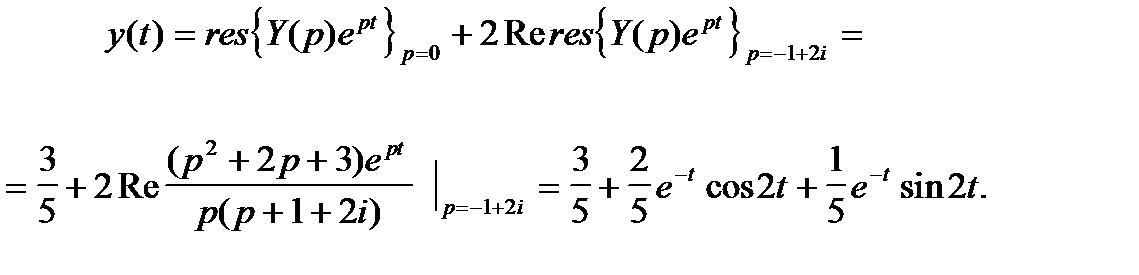
При решении операторным способом правая часть уравнения может быть задана функцией, имеющей точки разрыва 1-го рода.
Пример 6. Найти частное решение уравнения, для которого правая часть 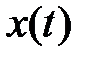 приведена на рис.
приведена на рис.
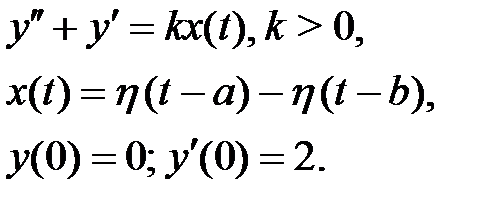
| а |
| a b |
| x(t) |
| t |
Переходя к изображениям:
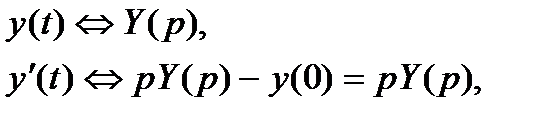
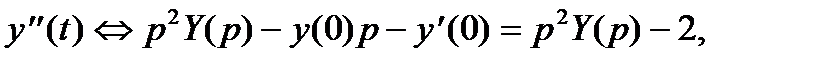
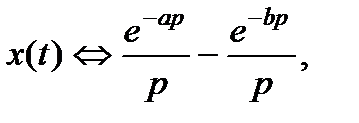
получаем алгебраическое уравнение

Тогда решение запишется в виде:
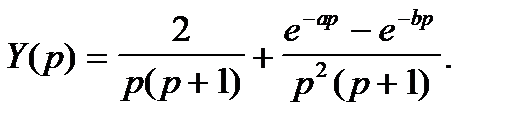
Переходя к оригиналам и используя свойство запаздывания оригинала, получаем решение:
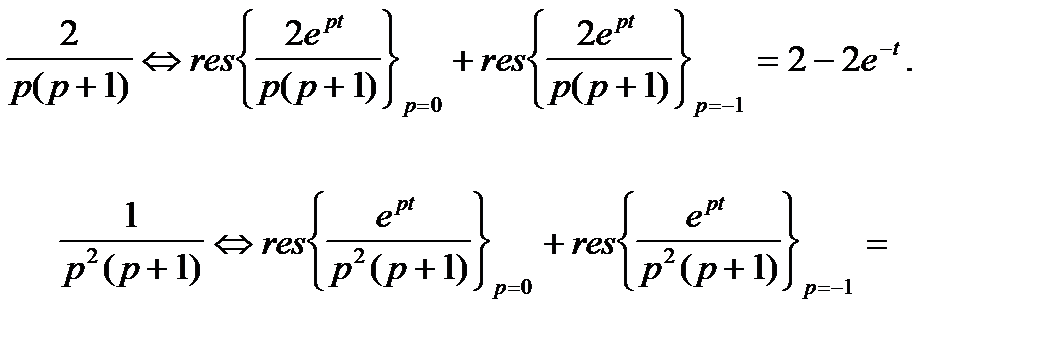
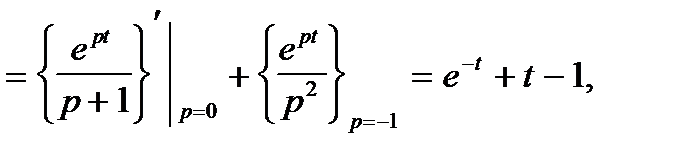
Результат записывается следующим образом:
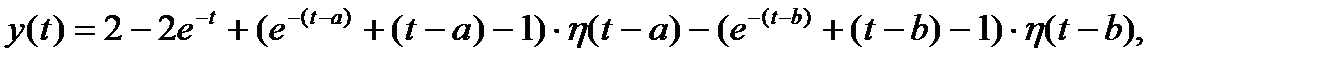

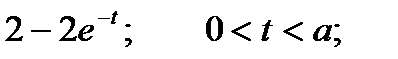

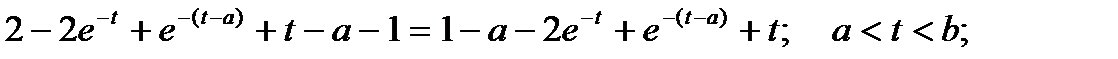
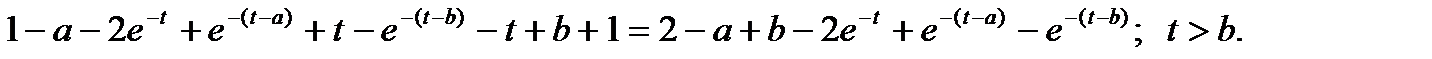
Date: 2015-09-24; view: 1667; Нарушение авторских прав