Решение систем линейных дифференциальных уравнений операторным методом

Рассмотрим систему линейных дифференциальных уравнений

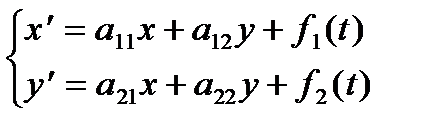
c начальными условиями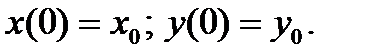

Считая функции 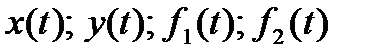функциями-оригиналами и переходя к изображениям, получаем систему алгебраических уравнений относительно переменных :

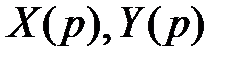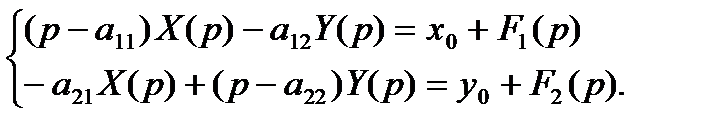
Решая эту систему методом исключений, методом Крамера или матричным методом, находим изображения 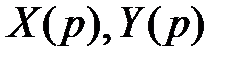. Возвращаясь к оригиналам, получаем решение:

Рассмотрим более подробно матричный метод решения полученной алгебраической системы, вводя следующие матрицы:

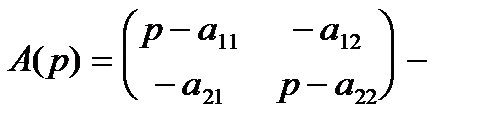матрица коэффициентов системы;

матрица искомых функций;

матрица, включающая начальные условия и изображения правых частей.

Исходная система записывается как матричное уравнение:

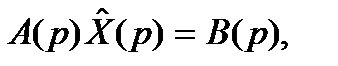
решением которого является матрица:

Здесь называется преобразователем Лапласа фундаментального решения системы или матрицей Грина. По правилу нахождения обратной матрицы получаем:

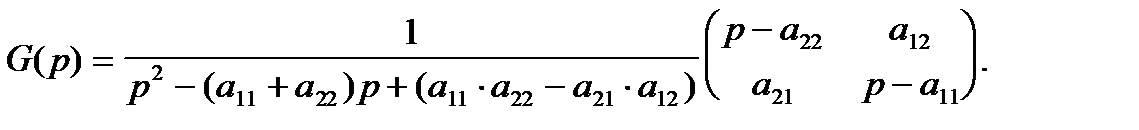
Оригинал 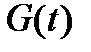матрицы называют матричной функцией отклика, фундаментальным решением или матричной функцией Грина:

.

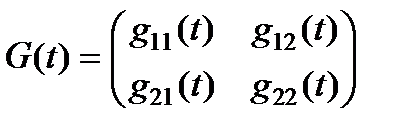Таким образом, решение системы записывается в виде матрицы:

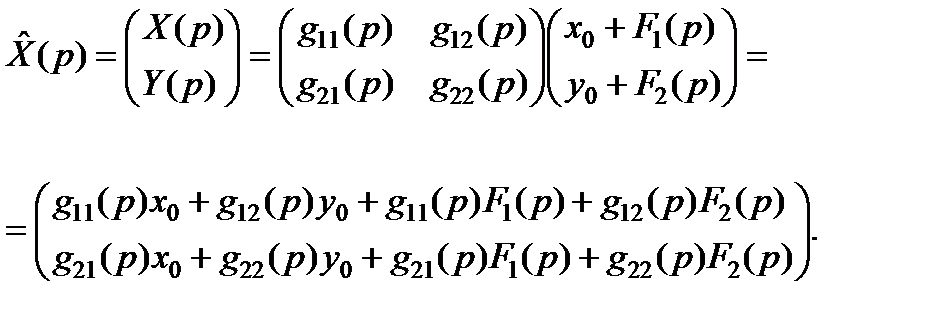
Переходя к оригиналам в каждой из строк этой матрицы, получаем окончательное решение системы:

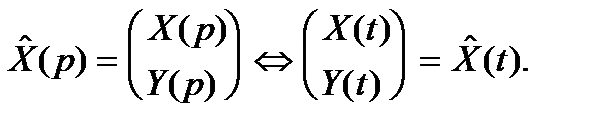
Пример 7. Найти решение системы дифференциальных уравнений:

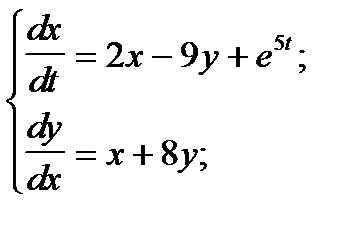
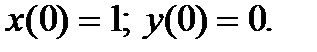
Переходя к изображениям:

получаем систему алгебраических уравнений:

Матрица 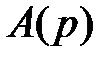этой системы имеет вид:

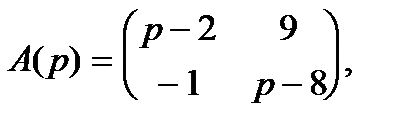
обратная матрица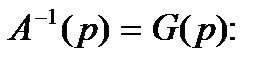

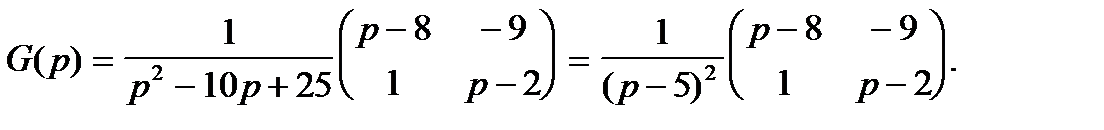
Введем матрицу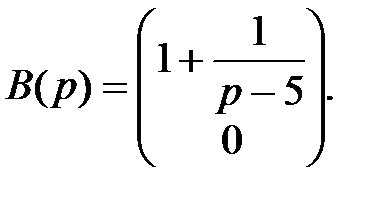

Решение системы имеет вид:

ЗАДАЧИ

1. Решите дифференциальные уравнения

	Условия задачи	Ответ

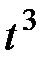
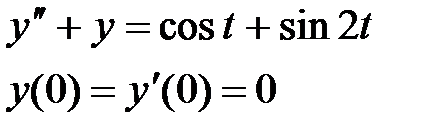
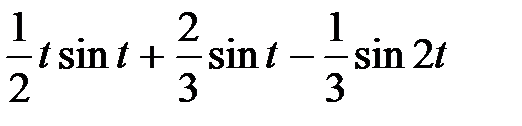
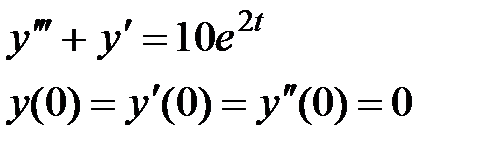
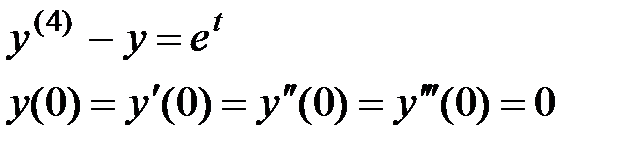
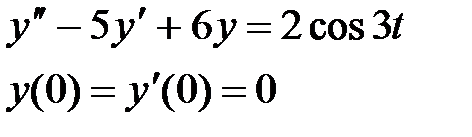
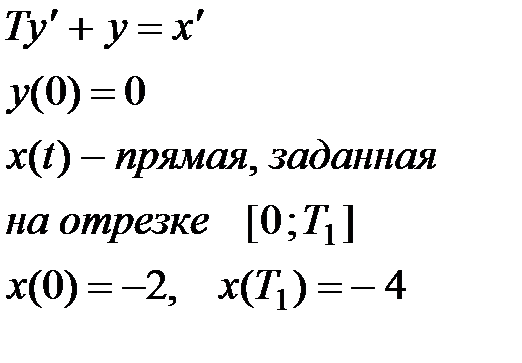
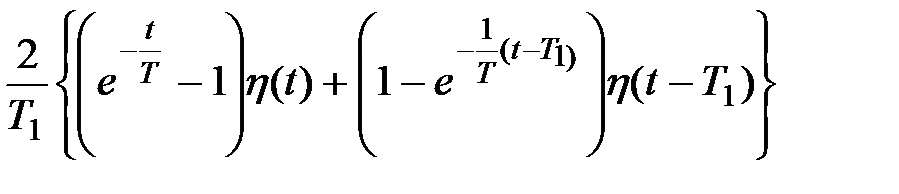
2. Решите системы линейных дифференциальных уравнений

	Система	Ответ

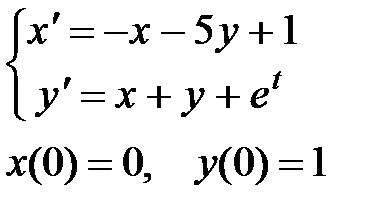
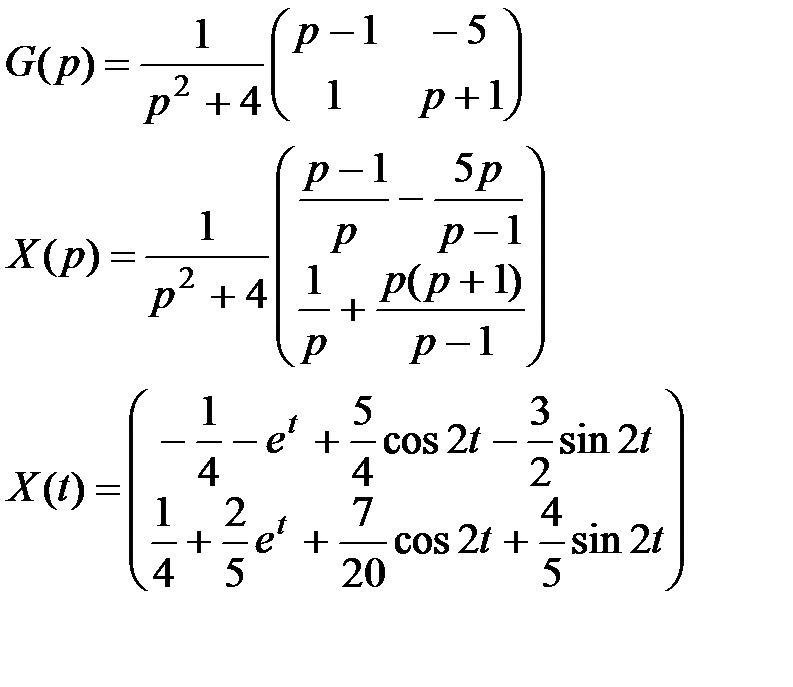
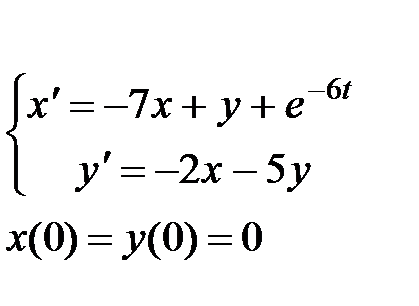
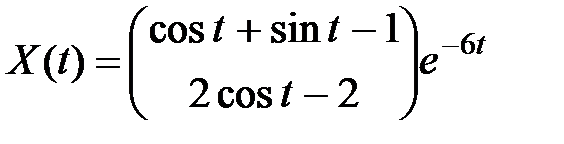
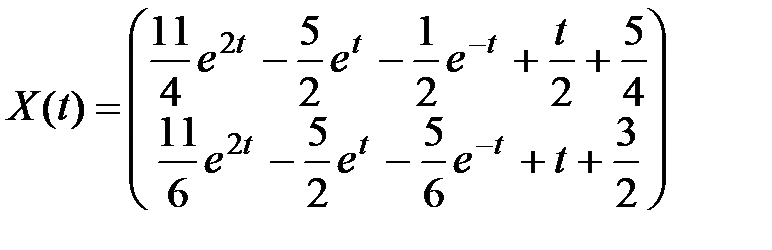
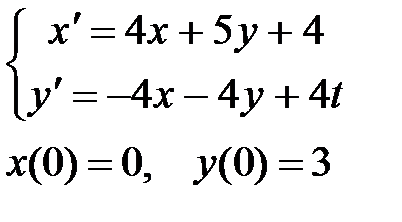
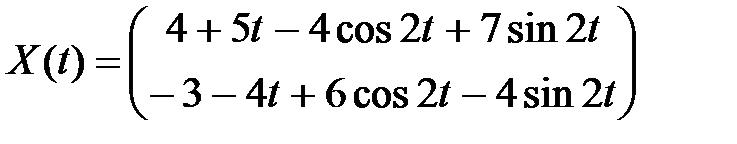
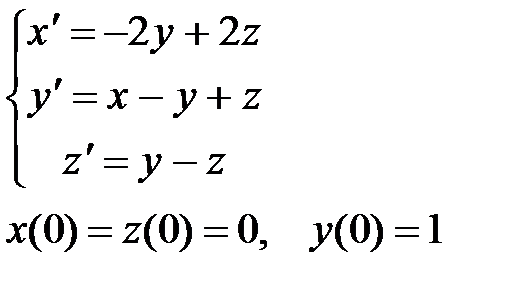
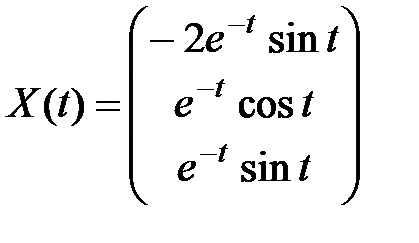
Date: 2015-09-24; view: 741; Нарушение авторских прав