Проверка гипотезы о виде распределения генеральной совокупности

Н а следующем этапе работы по виду полигона частот (гистограммы) и полученным значениям числовых характеристик выдвигаем гипотезу о виде распределения генеральной совокупности и проверяем соответствие данной гипотезы эмпирическим данным.

После того, как выдвинули гипотезу, находим теоретические частоты, соответствующие предполагаемому распределению:

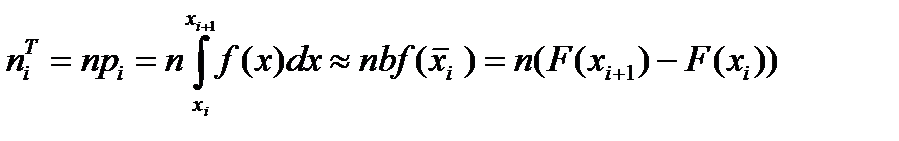
1. Нормальный закон распределения

Если полигон частот является симметричным, а числовые характеристики выборки удовлетворяют особенностям этого распределения

,

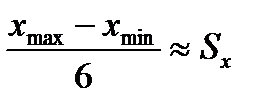то делаем предположение, что выборка получена из нормально распределенной генеральной совокупности. Этот закон имеет два параметра, оценки которых находим по выборке:

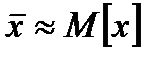- выборочное среднее приравниваем к математическому ожиданию,

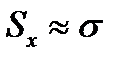- выборочное среднеквадратичное отклонение (стандарт) приравниваем к его теоретическому значению. Функция плотности вероятности для нормированной переменной приводят по таблице на стр.408 . Теоретическую частоту находим по формуле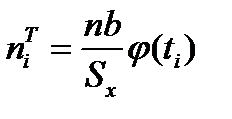

2. Показательный закон. Этот закон характеризуется одним параметром 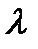, оценку которого находим по методу моментов, приравнивая выборочное среднее к теоретическому значению математического ожидания: , .

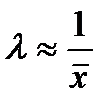Особенностью распределения является равенство единице коэффициента вариации 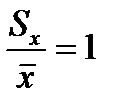. Теоретические частоты находим по формуле

1. Гамма распределение характеризуется двумя параметрами, оценки которых находим, приравнивая теоретические и выборочные моменты с учетом того, что

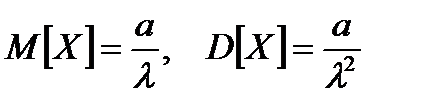, коэффициент вариации .

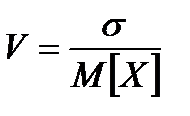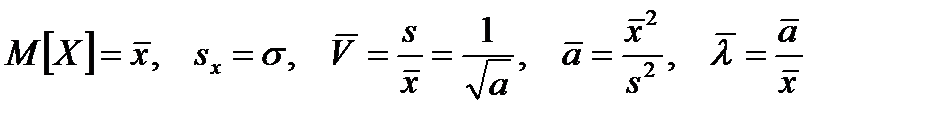
Оценку теоретической частоты находим по формуле

Значение гамма-функции находим по таблице (например, Г. Корн, Т. Корн Справочник по математике).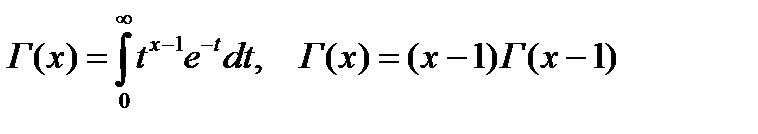

Полученные теоретические частоты наносим на полигон частот. Если согласие между эмпирическими и предполагаемыми теоретическими частотами визуально достаточно хорошее, то проводим проверку выдвинутой гипотезы по критерию 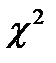(стр. 278-281). При этом выборочное значение статистики критерия находят по формуле 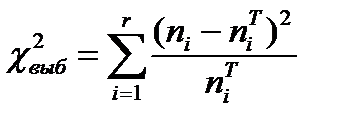. Здесь - число интервалов с учетом того, что 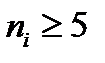. Если это условие не выполняется, то объединяем соседние интервалы. Теоретическое значение статистики критерия находим по таблице на стр. 412: 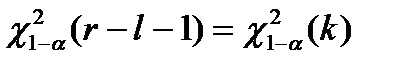. В этом выражении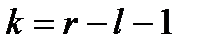 – число степеней свободы. Здесь 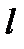- это число параметров распределения, оцениваемых по выборке. Так для показательного закона 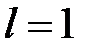, для нормального закона и гамма-распределения .

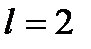Если выполняется условие 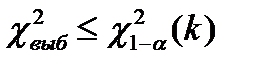, то выдвинутая гипотеза не противоречит опытным данным на заданном уровне значимости 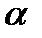и не может быть отвергнута.

Далее приведен пример сравнения эмпирического распределения, полученного по выборке, и нормального распределения

параметрами .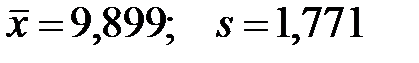

Date: 2015-09-24; view: 702; Нарушение авторских прав