
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 20
|
|
Раздел. Энергетические характеристики и подвижность дислокации, (продолжение). План
1. Первое и второе правила Франка.
2. Силы действующие на дислокации.
3. Приведенное напряжение сдвига,
4. Прогиб дислокационной линии,
В результате пересечения трёх и более дислокации образуется неподвижный дислокационный узел. Согласно первому правилу Франка
геометрическая сумма векторов Бюргерсав узле А равна нулю, т.е. 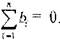
На рис. 20.1 показан дислокационный узел в точке А (а) и геометрическая суммавекторов Бюргерса пересекающихся дислокаций (в).
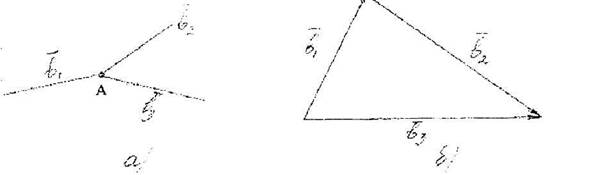
Рис. 20.1. Дислокационный узел в точке А
(а) н геометрическая сумма векторов Бюргерса пересекающихся дислокации (б)
Такой узел является неподвижным (устойчивым). Смещения атомов здесь скомпенсированы.(Первое правило Франка является аналогом правила Кирхгофа в электротехнике). Вектор Бюргерса точечного дефекта всегда равен нулю.
С целью уменьшения энергии дислокации могут понижать свой
вектор Бюргерса 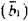 за счет расщепления полных дислокации на частичные (
за счет расщепления полных дислокации на частичные (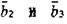 ). Такое расщепление возможно, если удовлетворяется второе правило Франка
). Такое расщепление возможно, если удовлетворяется второе правило Франка

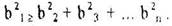
Это правило показывает, что дислокация п-кратной мощности неустойчива, т.к. 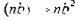 . При энергетическом равенстве реакция
. При энергетическом равенстве реакция
расщепления приводит к росту энтропии решетки и потому более вероятна.
Как мы уже видели ранее движение дислокации вызывает пластическую деформацию кристалла. Следовательно, дислокация при скольжении совершает работу. Поэтому можно представить, что на единицу длины дислокации действует некоторая сила F.
В общем случае на дислокацию действуют силы разного происхождения: внешние силы и внутренние от действия соседних дислокаций, точечных дефектов и других несовершенств. Пусть дислокация пробегает весь кристалл под действием касательных напряжений 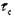 . Тогда
. Тогда
площадь скольжения будет равна l*d. На рис. 20.2 показана схема движения дислокации АВ под действием напряжения.

Рис. 20 1\ Схема движения дислокации под действием внешней напряжения
Совершаемая внешним напряжением работа над кристаллом приводящая к сдвигу, дает ступеньку на поверхности высотой в. Работу по
163 формоизменению кристалла можно определить как
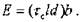
С другой стороны, работа по перемещению дислокации на величину d под действием силы F на. ед. длины равна
E'=(Fl)d
Учитывая, что работа внешних и внутренних сил должна быть равна, т.е. Е'=Е находим величину силы, действующую на ед. длины дислокации
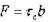
Эта сила перпендикулярна линии дислокации и направлена к той части плоскости скольжения, где сдвиг ещё не произошел. Эта формула полученная Питчем и Келлером показывает, что если на кристалл действуеч внешняя сила 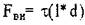 , то на дислокацию действует сила в "в" раз большая
, то на дислокацию действует сила в "в" раз большая
Таким образом, дислокации являются концентраторами напряжений, что является ещё одной из причин низкой прочности кристаллов. Очевидно, что напряжение 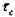 является приведенным напряжением сдвига действующим в
является приведенным напряжением сдвига действующим в
данной плоскости скольжения. Оно всегда меньше действующего на кристалл напряжения г. Из простых геометрических соображений
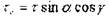
где а и у - углы между внешней силой и действующей системой скольжения (плоскостью и направлением) дислокации. На рис. 20.3 дана схема к расчету приведенных напряжений сдвига 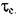
| 16 4 |

Рис. 20.3. Схема к расчету приведенных напряжений сдвига
Скалывающее напряжение 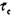 в системе скольжения достигает
в системе скольжения достигает
максимума равного 0,5 (а= у= 45°). Фактор Шмида - 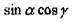 объясняет
объясняет
сильную ориентационную зависимость для кристаллов. Например, у кадмия (гексагональная сингония) 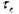 изменяется в 7 раз по разным
изменяется в 7 раз по разным
кристаллографическим направлениям. На рис. 20.4 показана зависимость скалывающего напряжения т. от величины фактора Шмида.
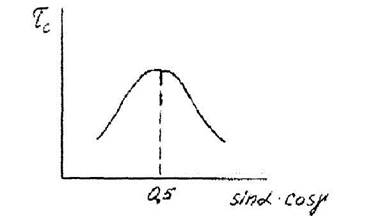
Рис. 20.4. Зависимость скалывающего напряжения 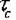 от величины фактора Шмида
от величины фактора Шмида
Рассмотрим изгиб дислокационной линии под действием внешних напряжений относительно узлов сетки дислокации. Прогибу дислокации будут препятствовать силы линейного натяжения. Очевидно, для прогиба радиусом 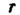 дуги дислокации потребуется определенное внешнее
дуги дислокации потребуется определенное внешнее
I h
напряжение 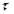 . Найдем связь между напряжениями и радиусом прогиба дислокации.
. Найдем связь между напряжениями и радиусом прогиба дислокации.
Пусть на элемент дуги 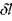 вдоль О А действует внешняя сила
вдоль О А действует внешняя сила 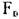 (Рис, 20.5).
(Рис, 20.5).
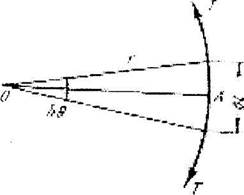
Рис. 20.5. Схема к расчету напряжения прогиба
дислокационной линии
Противодействующая ей сила от составляющих сил линейного натяжения - F' направлена навстречу внешней силы FB вдоль АО.
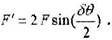
Здесь F - сила линейного натяжения. Для малых углов G имеем
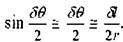
. Условие равновесия достигается в случае FBH= F',
т.е. 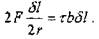
Или, учитывая, что 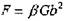
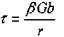
Это напряжения, необходимые для получения стабильной дуги дислокации радиусом г. С ростом г радиус прогиба уменьшается, достигая
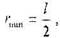
|
минимума равного
которому соответствует максимальное
напряжение 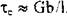
При циклическом изменении напряжения, если 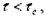 то дислокация
то дислокация
упруго изгибается возле положения равновесия. При 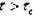 радиус
радиус 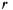 начинает
начинает
увеличиваться и условия равновесия нарушаются. Дислокационная линия будет самопроизвольно и необратимо расширяться, увеличивая площадь сдвига. На рис.20.6 а,6,в показаны разные фазы прогиба.
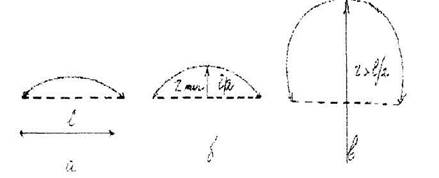
Рис 20.6 Прогиб дислокационной линии а, б, в - разные фазы прогиба
Таким образом, чем больше средний размер дислокационной сетки, тем при более низком критическом напряжении 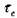 начинается необратимая
начинается необратимая
пластическая деформация, что хорошо подтверждают эксперименты. Укорочение дислокационных линий за счет небольшой деформации, выделений второй фазы (при старении) вызывает повышение прочности мет аи л а.
Выводы
1. Геометрическая сумма векторов Бюргерса в дислокационном узле
равна нулю.
2. Дислокации являются концентраторами напряжений в кристалле.
3. Чем больше средний размер дислокационной сетки, тем при более
низком критическом напряжении начинается пластическая деформация
Date: 2015-09-24; view: 482; Нарушение авторских прав