
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Равновесная концентрацня вакансий в разных металлах вблизи температуры плавления
|
|
| Металл | Аи | Ag | Си | А1 | РЬ | Na | Mg | Cd |
| 7,2 | 1,7 | 2,0 | 9,4 | 1,7 | 7,5 | 7,2 | 4,5 |
Действие радиации на кристалл создает в нем неравновесную концентрацию точечных дефектов. Кроме этого, облучение частицами высоких энергий сопровождается дополнительными явлениями: ионизация атомов, смещение частиц из положения равновесия, образование продуктов ядерных реакций (появление в кристалле атомов отличных от атомов основного вещества), тепловые клинья и клинья смещения ионов. На рис. 16.3 показан клин смещения в облученном кристалле. Стрелка показывает путь заряженной частицы, а пунктир - путь возбужденного иона.
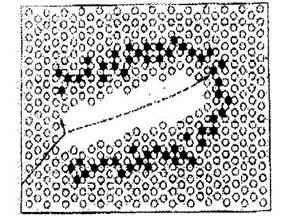
Рис. 16.3. Клин смещения в облученном кристалле
Движущаяся в решетке частица высокой энергии передает большую часть энергии ближайшим атомам, резко возбуждая их. Вдоль пути пробега частицы или выбитого ею из решетки атома, вещество сильно нагревается. Расчет показывает, что в узкой области содержащей несколько тысяч атомов, происходит очень быстрый нагрев до нескольких тысяч градусов. Столь же. быстрый спад температуры за 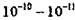 с создает закалочные дефекты - так
с создает закалочные дефекты - так
называемый клин смещения. Все эти нарушения структуры в результате облучения вызывают повышение твердости, скалывающего напряжения, прочности, констант упругости, рост электросопротивления, ускорение диффузии и др. Так например, графитизация в хромистом чугуне протекает десятки лет, а при облучении нейтронами - проходит за несколько минут.
В результате отжига происходит восстановление первоначальных свойств кристалла. Отжиг в основном приводит к рекомбинации вакансий и межузельных атомов.
Вывод
1. Равновесная концентрация дефектов соответствует
термодтнамически устойчивой системе. Неравновесная концентрация
дефектов фиксируется в случае ускоренных охлаждений.
2. Точечные дефекты приводят к повышению
электросопротивления, линейных размеров образца и понижению плотности
материала.
3. Действие радиации на кристалл создаёт в нём неравновесную
концентрацию точечных дефектов.
ЛЕКЦИЯ 17
Тема. Линейные дефекты
Раздел. Краевая и винтовая дислокации
План
1. Краевая и винтовая дислокации.
2. Напряжение Пайерлса.
3. Плоскость скольжения краевой и винтовой дислокаций.
4. Смешанная дислокация.
Как уже говорилось, низкое скалывающее напряжение в реальных металлах обусловлено тем, что в смещении участвуют не все атомы одновременно по обе стороны от плоскости скольжения, как при жестком сдвиге, но лишь небольшая группа атомов в области края экстраплоскости дислокации. Смещение атомов при скольжении краевой дислокации справа налево на один параметр решетки показано на рис.17.1.
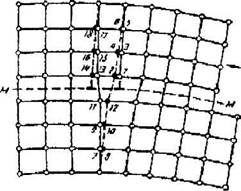
Гис. 17.1. Смещение атомов при скольжении краевой дислокации справа налево на один
параметр решетки
Видно, что незначительные перемещения атомов от положений равновеccия в области края экстраплоскости приводят к перемещению дислокации на одно межатомное расстояние. Такое движение дислокации наз. скольжением или консервативным движением (без переноса массы вещества и изменения объема, когда атомы остаются возле своих положений равновесия).
Развитие сдвига при движении дислокации в кристалле можно уподобить перемещению ковра из положения АВ в положение А'В' за счет продвижения вдоль него складки. В этом случае требуется меньшее усилие, чем при протаскивании по полу всей площади ковра, хотя конечный результат один и тот же (рис. 17.2).

|
Рис. 17.2. Перемещение ковра из положения АВ в положение А В в результате продвижения складки
Аналогичной складкой на теле перемещаются змеевидные, проталкивая её от хвоста к голове.
В зависимости от положения линии дислокации относительно вектора сдвига различают дислокации краевые, винтовые и смешанные.
В нашем случае линия дислокации была перпендикулярна вектору сдвига - это краевая дислокация. Условно их делят на положительные и отрицательные. При выходе дислокации на поверхность кристалла наблюдаются линии сдвига (подобно сдвигу в колоде карт). Сдвиг обычно идет по плотноупакованным плоскостям и направлениям. Для ГЦК: (111), для ГП-(0001):
Решая задачу движения краевой дислокации в периодическом потенциальном поле атомов "подложки", Пайерпс и Набарро показали, что при Т=0К напряжения трения решетки (напряжения Пайерлса) составляют:
(17.1)
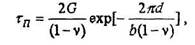
где v - коэффициент Пуассона, 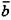 - вектор сдвига, d- ширина дислокации, характеризующая протяженность поля искажений решетки вокруг дислокации. В ГЦК металлах d- велико (до ЗО-5Оb) и значение
- вектор сдвига, d- ширина дислокации, характеризующая протяженность поля искажений решетки вокруг дислокации. В ГЦК металлах d- велико (до ЗО-5Оb) и значение 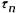
будет мало. В О ЦК металлах наоборот, ширина дислокации составляет всего d= l-5b и напряжения трения довольно велики. Из формулы (17.1) видно, что по плотноупакованным направлениям, по которым величина вектора Бюргерса минимальна минимальна, 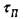 понижается (межатомные
понижается (межатомные
связи меняются незначительно при переходе от одной конфигурации атомов к другой). Для винтовой дислокации в формуле (17.1) отсутствует множитель (1-у),такчто 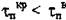 При d = (l-2)b,
При d = (l-2)b, 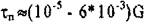
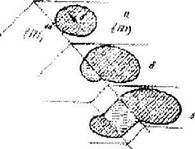
Понятие о винтовой дислокации ввел Бюргере (1939г.). Она образуется при сдвиге надрезанного по плоскости АВСД кристалла, как это показано нарис. 17.3.
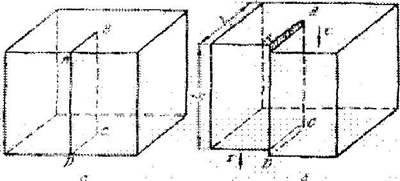
Fhc. 17.3. Сдвиг, создающий винтовую дислокацию а-кристалл до сдвига надрезан по плоскости АВСД б -кристалл после сдвига, АВСД - зона сдвига
Плоскость надреза при действии касательных напряжений будет являться зоной сдвига. Граница зоны сдвига ВС является линией винтовой дислокации, параллельной вектору сдвига.
Верхняя атомная плоскость оказывается изогнутой. После сдвига на параметр решетки бывшие ранее параллельные атомные плоскости превращаются в винтовую или геликоидальную поверхность, осью которой является линия дислокации (рис. 17.4).
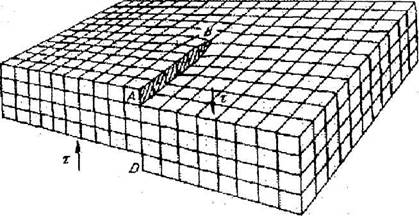
Рис. 17.4. Винтовая дислокация, представляющая собой атомную плоскость, закрученную в виде геликоида
Винтовая дислокация как и резьба винта может быть правой и левой. Область несовершенства здесь простирается вдоль линии ВС, в то время как вдали от линиидислокации решетка остается практически без искажений.
Область вдоль линии дислокации ВС, где смещения атомов превышают упругие, называют ядром дислокации. Радиус ядра составляет 1-2 параметра решетки. Строеве ядра изучено очень слабо, т.к. здесь нельзя использовать обычную теорию упругости.
У винтовой дислокации нет однозначной плоскости сдвига. Она может скользить в любой плотноупакованной кристаллографической плоскости, содержащей линию дислокации и вектор сдвига, т.е. легко переходить скольжением из плоскости в плоскость. Такой процесс называется поперечным скольжением (двойным или множественным) винтовой дислокации. Двойное поперечное скольжение винтовой дислокации ВС показано на рис. 17.5.
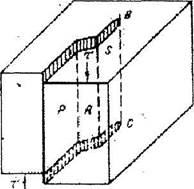
Рис. 17.5. Двойное поперечное скольжение винтовой дислокации ВС
Причиной поперечного скольжения могут быть встечающиеся барьеры на пути движения дислокации в первоначальной плоскости или изменение направление вектора приложенных напряжений. В то же время, плоскость скольжения у краевой дислокации строго определена линией дислокации и вектором сдвига.
Обычно в кристалле дислокации редко бывают чисто краевыми или чисто винтовыми. В большинстве случаев они смешанные (рис, 17.6).

Рис. 17.6. Смешанная дислокация AC
АС - смешанная дислокация. В области точки С - дислокация имеет краевую ориентацию. Вблизи точки А - винтовую. Скорость V движения винтовой и краевой компонент различны, т.к. различаются напряжения Пайереса, поэтому на поверхность кристалла они выходят не одновременно. Например, в кристалле LiF Гилманом было обнаружено, что  Линия
Линия
дислокации всегда является ступенчатой. Высота ступенек или порогов кратна параметру решетки.
Расположение атомов вдоль линии смешанной дислокации АС показано на рис. 17.7.
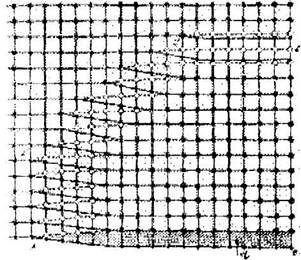
Рис. 17.7. Расположение агомов в области смешанной дислокации
| Рис. 17.8. Поперечное и двойное поперечное скольжение петли смешанной дислокации в ГЦК решетке |
Смешанная дислокация в общем случае не лежит в одной плоскости. Такая дислокация может образовывать и замкнутую петлю, не лежащую в одной плоскости. Из-за наличия участков с винтовой ориентацией дислокационная петля может совершать поперечное скольжение. На рис.17.8. показана дислокационная петля» распространяющаяся в плотноупакованной плоскости типа (111) ГЦК решётки.
Встречая барьер она может совершить поперечное скольжение в другую плотноупакованную плоскость. На рисунке видно, как участок петли вблизи точки т, имеющий винтовую ориентацию, из-за встречи с препятствием в плоскости (111), переходит новую плоскость (111) (рис. 17.7,6). Затем, пройдя барьер, участок петли с винтовой компонентой способен перейти в плоскость параллельную первоначальной плоскости скольжения (111) (рис. 17.7,в). Многократное повторение этого процесса называют множественным поперечным скольжением. В общем случае линия смешанной дислокации и поверхность скольжения не лежат в одной плоскости.
Выводы
1. В зависимости от положения линии дислокации относительно
вектора сдвига различают дислокации краевые, винтовые и смешанные.
2. По плотноупакованным направлениям напряжение Пайерлса
минимально.
3. У винтовой дислокации нет однозначной плоскости сдвига, в
отличие от краевой дислокации.
4. Винтовая дислокация может поперечное скользить консервативным
путем из одной плоскости в другую, встречая барьеры или стопоры на своем
пути.
ЛЕКЦИЯ 18
Раздел.Краевая и винтовая дислокации (продолжение)
План
1. Вектор и контур Бюргерса.
2. Обозначение вектора Бюргерса.
3. Неконсервативное движение дислокации.
4. Призматические дислокаций.
Вектор Бюргерса является как геометрической, так и энергетической характеристикой дислокации. Это мераупругих искажений решетки, которые связаны с присутствием дислокации. Вектор сдвига, определявший ранее величину и направление смещение атомов в области сдвига - это есть вектор Бюргерса. Но, как уже говорилось, дислокации не всегда образуются действием внешних напряжений и тогда наблюдать величину сдвига (ступеньки на поверхности кристалла) нельзя. Поэтому необходимо в общем случае оценить величину искажений решётки за счет присутствия в ней дислокации.
Вокруг дислокации в области "хорошего" кристалла (на расстоянии не менее 10-15 параметров решетки) мысленно проводим замкнутый контур (контур Бюргерса) произвольной (выпуклой) формы из любого узла решетки. На рис 18.1 показан контур Бюргерса вокруг краевой дислокации (а) и эквивалентный контур в совершенном кристалле (б).
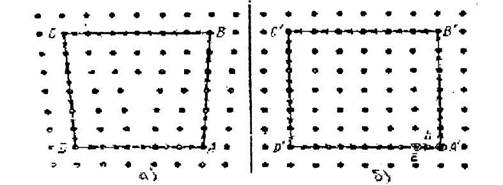
Рис. 18.1. Контур Бюргерса вокруг краевой дислокации (а) и эквивалентный контур в совершенном кристалле (б)
Такой же контур построен вокруг линии винтовой дислокации и в кристалле без дислокации (рис.18.2).
Ст. т.
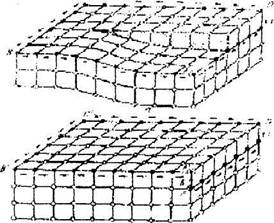
Рис. 18.2. Контур Бюргерса вокруг ABCD, полученная вдавливанием эквивалентный контур в
области"хорошего" кристалла (б)
Контур, построенный в идеальной решетке, оказывается незамкнутым. Вектор Бюргерса 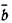 - замыкающий вектор (вектор невязки). Он равен или кратен, кратчайшему межатомному расстоянию.
- замыкающий вектор (вектор невязки). Он равен или кратен, кратчайшему межатомному расстоянию.
Величина вектора Бюргерса не зависит от размеров контура
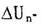
|
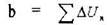
|
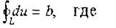
|
или
смещение n-oro атома от
положенияравновесия.
Это означает, что чем дальше от дислокации, тем больше протяженность контура, но меньше смещение атомов и, наоборот. Действи-

тельно, число атомов n, по которым проводится контур Бюргерса, пропорционально расстоянию от дислокации r. В то же время, смещения атомов 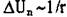 (см. ниже), так что
(см. ниже), так что
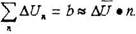
Контур, проведенный вокруг двух дислокации, даст вектор Бюргерса, равный сумме векторов Бюргерса этих дислокации. Вектор Бюргерса обозначается как
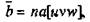
где а - параметр ячейки, [uvw]- кристаллографическое направление вектора Бюргерса, n- целая или дробная доля параметра решетки. Модуль вектора Бюргерса равен:
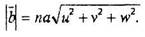
Рассмотрим формулу записи трех векторов Бюргерса 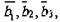 в
в
| Рис. 18.4. Векторы Бюргерса в примитивной кубической решетке |
примитивной кубической решётке (Рис. 18.4).
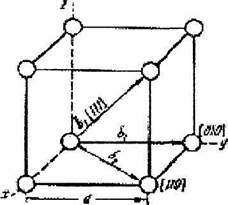
Для вектора 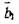 составляющие по осям равны:
составляющие по осям равны: 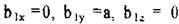 Таким образом,
Таким образом,
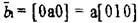 . Мощность вектора
. Мощность вектора 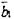 будет равна:
будет равна:
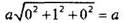
Для вектора 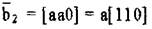 и его мощность
и его мощность 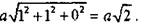
Date: 2015-09-24; view: 666; Нарушение авторских прав