Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Показатели вариации и методы их вычисления
|
|
Средняя величина не дает представления о том, как отдельные значения изучаемого признака располагаются вокруг средней и насколько однородна изучаемая совокупность. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность. В других случаях, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность. Колеблемость (колебание, рассеивание) отдельных значений характеризуют показатели вариации (лат. variatio –изменение, колебание, различие).
Пример. В следственных отделах работает две группы следователей, каждая из трех человек. На начало месяца у каждого следователя находилось в производстве следующее количество уголовных дел: в первой группе – 8, 10, 12; во второй группе − 1, 10, 19. Средняя нагрузка на одного следователя в обеих группах равна (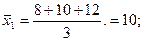
), хотя в первой группе различия в следственной нагрузке значительно меньше, чем во второй.
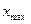и наименьшим 
значениями вариантов: 
. В нашем примере размах вариации следственной нагрузки составляет: в первой группе следователей 
дела, а второй группе 
дел. Различие значительное: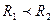 
в 4,5 раза. Это свидетельствует о том, что в первом случае совокупность более однородна и средняя следственная нагрузка первой группы следователей более показательна.
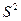(от лат. dispersio – рассеяние, разброс) – мера рассеивания от среднего. Дисперсия – это среднее арифметическое из квадратов отклонений величин 
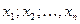от их среднего арифметического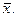 
Формула для вычисления дисперсии простой:
Формула для вычисления дисперсии взвешенной: 
Существенным недостатком дисперсии является то, что она измеряется в квадратных единицах изучаемого признака, что практически всегда не имеет смысла. 3. Среднее квадратическое отклонение 
– корень квадратный из дисперсии 
Выражается оно в тех же единицах измерения, что и признак. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. 4. Коэффициент осцилляции отражает относительный разброс крайних значений признака вокруг средней. Формула для вычисления коэффициента осцилляции: 
5. Коэффициент вариации используется для оценки типичности средних величин. Формула для вычисления коэффициента вариаци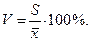и: 
Если 
то говорит о сильных отклонениях изучаемой совокупности от своего среднего значения, то есть колеблемость большая. Задача 7. По данным УМВД распределение осужденных в области за изучаемый период по возрастным группам было следующим (табл. 15). Определите: 1) дисперсию и среднее квадратическое отклонение; 2) коэффициент вариации.
Таблица 15
| Возраст, лет | До 20 | 20–25 | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 | 50 и старше |
| Число осужденных |
Решение. Учитывая, что уголовная ответственность по большинству преступлений в России наступает с 16 лет, а средняя продолжительность жизни по данным за 2011 год – 68 лет, дополним таблицу серединами интервалов возрастных групп.
| Возраст, лет | 16–20 | 20–25 | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 | 50–68 |
| Центр интервалов, лет | 22,5 | 27,5 | 32,5 | 37,5 | 42,5 | 47,5 | ||
| Число осужденных |
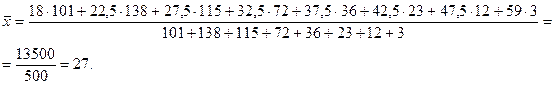По формуле дисперсии взвешенной имеем: 
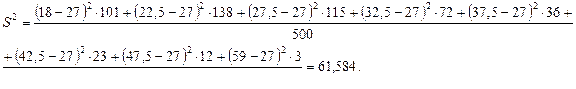Вычислим среднее квадратическое отклонение: 
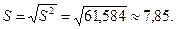Вычислим коэффициент вариации: 
Значения изучаемого признака достаточно плотно группируются около своего среднего.Date: 2015-09-22; view: 1049; Нарушение авторских прав