Статистические ряды распределения

Группировка, выполненная по одному признаку, называется простой. Среди простых группировок особо выделяют ряды распределения. Статистические ряды распределения – это упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Ряды распределения, построенные по качественным признакам называются атрибутивными. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Примером атрибутивного ряда может служить распределения осужденных по полу, занятости, национальности и т.д. Атрибутивный ряд распределение следов преступлений представлен в таблице 1. Примером вариационного ряда может служить распределение осужденных по возрасту, числу судимостей т.д. Вариационные ряды по способу построения бывают дискретными и интервальными.

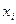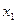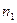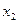Дискретным вариационным рядом (ДВР) называется такой вариационный ряд, в котором значения признака заданы в виде отдельных конкретных чисел. Варианта – отдельное значение признака, т.е. наблюдаемые значения . Если наблюдалось раз, наблюдалось 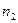раз, …, наблюдалось раз, причем , (n – объем статистической совокупности), то числа n_i называют частотами. А отношение частоты к объёму статистической совокупности, т.е. 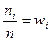– относительными частотами (или частостями), причем 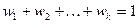. Значение вариант и соответствующие им частоты или относительные частоты можно записать в виде таблицы 4, называемой дискретным вариационным рядом.

Таблица 4

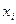
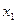
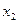
Варианта			…	xk
Частота	n1	n2	…	nk
Относительная частота			…

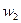
Задача 1. По данным УМВД имеются следующие данные о возрасте лиц, совершивших кражу в области за изучаемый период (табл. 5). На основе этих данных постройте дискретный вариационный ряд.

Таблица 5

Решение. В задаче рассматривается количественный признак – возраст правонарушителей. Для построения ДВР необходимо для каждого возраста (варианты) найти число его повторений в исходной таблице (частоту). Варианта 8 лет повторяется в данной совокупности 6 раз; 9 – 4 раза; 10 – 5 раз; 11 –6 раз; 12 – 10 раз; 13 – 11 раз; 14 – 18 раз; 15 – 12 раза; 16 – 8 раз. ДВР представлен в таблице 6.

Таблица 6

Возраст нарушителей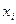
Количество нарушителей
Доля нарушителей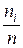

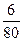
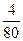
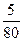
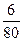
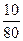
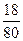
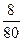
Интервальным вариационным рядом (ИВР) называется вариационный ряд, значения признака в котором заданы в виде интервалов.ИВР представлен в таблице 7.

Таблица 7

Частичный интервал			…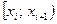
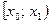
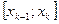
Частота	n1	n2	…	nk
Относительная частота wi	w1	w2	…	wk

ИВР строится по следующему правилу:

1. Определение числа групп 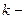производятся или, исходя из условия задачи, обычно 6 £ k £ 20, или по формуле Стерджеса: 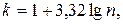где объем статистической совокупности.

2. Определение длины интервала группировки определяется по формуле: где 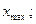наибольшее и наименьшее значения признака в совокупности. Если окажется, что h - дробное число, то рекомендуют округлить его в большую сторону. Обычно, интервалы берутся одинаковыми по длине, при этом левая граница интервала включается, а правая нет, исключением является только последний интервал, в котором правая граница включается.

3. Определение границ интервалов производится следующим образом: За начало первого интервала берут величину 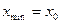, а все следующие границы вычисляются по формуле: .

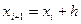4. Вычисление частот , путем подсчета значений признака из таблицы, входящих в данный интервал. По частотам находят относительные частоты.

5. Составление ИВР.

Задача 2. На основе данных – числа раскрытых преступлений по 100 РОВД за истекший месяц (табл. 8) постройте интервальный вариационный ряд.

Таблица 8

Решение. Объем статистической совокупности n =100. Используем правило построения ИВР.

1. Определим число групп:

2. ;

3. ,

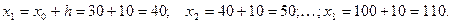
4. Вычислим частоты, для этого просматривают все значения признака, и определим число его значений, попавших в тот или иной интервал. Найдем относительные частоты.

5. Составим интервальный вариационный ряд (табл. 9).

Таблица 9

Интервалы числа преступлений,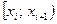
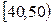
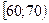
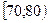
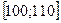
Число РОВД,

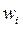
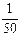
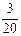
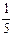
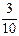
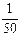
Замечание. Как правило, интервалы с малыми частотами (меньше 5) рекомендуют объединять с соседними.

Date: 2015-09-22; view: 1538; Нарушение авторских прав