Определение, параметры и матричное представление кодов Рида-Соломона

Коды Рида-Соломона (РС-коды) являются дальнейшим развитием БЧХ-кодов и в связи с высокой корректирующей способностью широко применяются в осовремененных системах связи, обработки информации, записи и воспроизведения информации. РС-коды – это такие БЧХ-коды, у которых мультипликативный порядок алфавита символов кодовой последовательности делится на длину кода. При α = 1 поле символов GF(g) совпадает с полем локаторов ошибок GF(g^а). Поскольку поле символов и поле локаторов ошибок совпадает, то все минимальные полиномы линейны. Чаще всего корни α образующего полинома Р(х) РС-кодов выбираются примитивными [1-4,7,8].

Образующий полином РС-кода записывается в виде произведения двучленов (х-α^ji), т. е. Р(х) = ∙ … ,

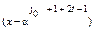где j₀ – любое целое положительное число (j₀ ≥ 1), α – корни полинома;

t – кратность (длина) корректируемых ошибок. РС-коды допускают выбор любого значения j₀, но при разумных значениях j₀ возможно уменьшение сложности реализации кодека. Максимальная степень образующего полинома 2∙t. Следовательно, проверочные символы и параметры кода «n» и «k» связаны равенством l = 2t = (n-k), двоичных символов.

К основным параметрам РС-кодов, корректирующих одиночные пакеты ошибок длиной t_n двоичных символов, относятся:

n = t_n (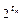 + 1) – длина кодовой последовательности;

k = t_n (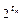 – 1)– количество информационных символов, входящих в кодовую последовательность;

l = 2t_n – количество поверочных символов;

d₀ = n-k=2t_n+1 – минимальное кодовое расстояние. РС-коды относятся к помехоустойчивым кодам с максимальным значением d₀;

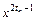
Р(х) = + – образующий полином.

Кодирование информационного сообщения Q(x) = x^k-1+x^k-2+…+1 и декодирование кодовых последовательностей F(x) = x^n-1+x^n-2+…+1 осуществляется с помощью соответственно порождающей матрицы G_k,n(x) и проверочной матрицы H_l,n(x), что в общем виде можно записать так:

F(x) = Q(x)×G(x) – кодирование информации,

S(x) = F'(x)×H(x) – декодирование информации.

Для того чтобы в процессе кодирования Q(x) кодовые последовательности F(x) получались систематического вида, необходимо использовать каноническую порождающую матрицу, т. е. матрицу вида G_k,n(x) = [I 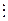H], а также использовать транспонированную проверочную матрицу, т.е. матрицу вида H_n,l(x)=[H^T 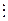I].

При несистематическом кодировании информации РС-кодами информационный полином Q(x) умножается на образующий полином Р(х), т. е. F(x) = Q(x)∙Р(х), при этом предполагается, что k > l, т. е. когда k < l целесообразнее при кодировании Q(x) использовать проверочный полином h(x) степени «k».

Систематическое кодирование информационных сообщений Q(x) производится во временной области и в этом случае декодирование кодовых последовательностей F(x) можно выполнять как во временной, так и в частной области, а также возможно смешанная реализация алгоритмов декодирования. По стандарту на цифровую запись и воспроизведение информации и при использовании помехоустойчивого кодирования проверочные символы размещаются внутри кодовой последовательности F(x).

С целью минимизации сложности рассмотрения принципа построения кодека циклического РС-кода принимаем, что РС-код корректирует одиночные пакеты ошибок кратностью t_n двоичных символов. В соответствии с [3,4] проверочная матрица двухизбыточного циклического РС-кода корректирующего одиночные пакеты ошибок кратностью t_n двоичных символов имеет следующее построение

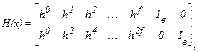(3.31)

где h⁰ = I_В – единичная матрица размерностью t_n ´ t_n.

Пакет ошибок кратностью t_n двоичных символов рассматривается как q-значный разряд, принимающий одно из «q» значений от «0» до «q-1». В этом случае в проверочной матрице (3.31) элементами столбцов являются не двоичные символы «1» и «0», а подматрицы вида 0; 1; h^β, значения которых определяются выражением вида

(3.32)

где 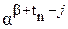– столбец подматрицы, соответствующий остатку от деления 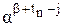(или ) на образующий полином Р(х) степени t_n;

β – показатель степени матрицы, который может находиться в пределах 1 ≤β ≤ .

Если в качестве образующего полинома выбран неприводимый примитивный полином степени t_n, то можно образовать различных матриц вида h^β.

Проверочная матрица Н(х) вида (3.31) может быть преобразована путем нормализации, а именно путем перемножения каждого элемента столбца матриц h^β на инверсию его первого элемента, т.е. следующим образом

(3.33)

В этом случае проверочная матрица Н(х) вида (2.34) будет иметь следующее построение

(3.34)

Порождающая матрица G(x) циклического РС-кода может быть построена по правилу

G_n,k(x) = [I_B:H^T(x)], (3.35)

где I_B – единичная подматрица размерностью k ´ k;

H^T(x) – транспонированная проверочная подматрица размерностью k ´ l.

Date: 2015-09-22; view: 799; Нарушение авторских прав