Определение, параметры, матричное представление и основные алгоритмы декодирования кодов

В соответствии с [1-3,5-9] коды Рида-Маллера (КРМ) относятся к групповым несистематическим (неразделимым) кодам с простым способом задания. Декодирование КРМ чаще всего реализуется мажоритарным и синдромным способами, однако возможно декодирование кодов по максимуму правдоподобия. В общем, КРМ эквивалентны циклическим кодам с добавлением общей ошибки на четность. Достоинствами данных кодов являются простота их задания и минимальная сложность реализации алгоритмов кодирования и декодирования. Недостатком КРМ является слабая (низкая) корректирующая способность; данные коды чаще всего применяются для коррекции ошибок кратностью не более трех двоичных символов.

Сущность КРМ и, следовательно, их определение состоит в следующем [3,7,8]: пусть F₀(х) есть кодовая последовательность (кодовый вектор), состоящая из одних логических единиц (1), а кодовые последовательности F₁(х), F₂(х),…, F_m(х) образуют строки матрицы, столбцами которой являются все двоичные наборы длиной m двоичных символов; m может иметь разное значение (величину), т.е. величина m ≥ 2. В этом случае для любых целых чисел m и Е (Е< m) можно построить помехоустойчивый код длины n=2^m двоичных символов, который называется кодом Рида-Маллера Е-го порядка. В реальных системах связи КРМ с Е > 3 практически не используется.

КРМ Е-го порядка содержит в качестве базиса (основы) кодовые последовательности F₀(х), F₁(х),…, F_m(х) и все поэлементные (покомпонентные) произведения Е или меньшего числа этих последовательностей. В данном определении поэлементные произведения кодовых последовательностей (условно: а = (а₁а₂…а_n) и b = (b₁b₂…b_n)) задается формулой а∙b = (а₁∙b₁,а₂∙b₂,…,а_n∙b_n). КРМ Е-го порядка дуален (двойственен) помехоустойчивому коду (m-E-1) порядка.

КРМ Е-го порядка длины n=2^m двоичных символов задается (строится) порождающей матрицей вида [3,4,6]:

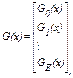(3.20)

где G₀(x) – кодовый вектор (кодовая последовательность) длиной n=2^m двоичных символов, состоящих из одних «l»;

G₁(x) – матрица размерности (m*2^m), содержащая в качестве столбцов все двоичные m-последовательности;

G_E(x) – матрица, строки которой получаются из строк матрицы G₁(x) как все возможные произведения Е строк матрицы G₁(x); для определенности обычно принимают, что первый столбец в G₁(x) состоит из одних «0», а последний из одних «1».

Коды Рида-Маллера имеют простые выражения для определения основных параметров данных кодов, а именно:

n=2^m двоичных символов – длина кодовой последовательности;

k=∑·Cⁱ_m двоичных символов – длина или количество информационных символов;

d₀=2^m-E – минимальное кодовое расстояние;

– кодовое расстояние.

Кроме того, возможно определение параметров КРМ по следующей методике:

– длина кодовой последовательности определяется рангом порождающей матрицы, т. е. n=2^m двоичных символов;

– параметры k и l=n-k КРМ Е-го порядка можно определить, используя следующие выражения:

(3.21)

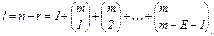(3.22)

Далее установим связь КРМ с другими линейными блоковыми кодами.

КРМ нулевого порядка (Е = 0) является (n,k) = (n,1) -кодом и соответствует коду с повторением и использует мажоритарный алгоритм декодирования. Минимальная кодовое расстояние такого кода равно d₀ = 2^m, а так как в этом случае m = 2, то d₀ = 2² = 4.

КРМ первого порядка (Е = 1) тесно связаны с кодами максимальной длины, которые, в свою очередь, дуальны кодам Хэмминга. Если начать построение помехоустойчивого кода максимальной длины и расширять его путем добавления общей проверки на четность, то получим ортогональный код. Данный код имеет длину n = 2^m двоичных символов и вес каждой ненулевой кодовой последовательности равен w_i = d = 2^m-1. Следовательно, любые две кодовые последовательности совпадают в 2^m-1 позициях и различаются в остальных 2^m-1 позициях. Используя этот код с противоположными сигналами, получим множество из 2^m ортогональных сигналов для 2^m кодовых последовательностей; отсюда и название ортогональных сигналов.

КРМ первого порядка получаются непосредственно из ортогонального кода добавлением кодовой последовательности состоящей целиком из «1». Если же рассматривать передаваемые сигналы, то эта процедура эквивалентна добавлению дополнительных сигналов к первоначальному множеству ортогональных сигналов. По этой причине полученный код называют биортогональным кодом [3,4].

Рассмотрим принцип построения КРМ с использованием следующих исходных данных кода: m = 4 и Е = 3. Следовательно, необходимо определить все параметры КРМ третьего порядка. Далее определяем параметры кода n,k,d₀:

n = 2^m = 2⁴ = 16 двоичных символов – длина кодовых последовательностей;

двоичных символов – длина информационного блока; d₀=2^m-E= 2^4-3=2.

Данный КРМ задается порождающей матрицей вида

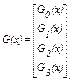(3.23)

Строим порождающие матрицы G₀(x),G₁(x),G₂(x),G₃(x).

Порождающая матрица G₀(x) содержит одну строку (обозначим эту строку буквой а₀) логических единиц с количеством равным n = 2^m = 2⁴ = 16 двоичных символов и имеет следующий вид:

G₁(x) = [1111111111111111] = [а₀].

Порождающая матрица G₁(x) содержит m=4 строки; первая строка матрицы содержит 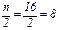логических нулей (0) и логических единиц (1). Последующие строки данной матрицы строятся аналогичным способом, т. е. делением последовательностей 1 и 0 строк на два. Порождающая матрица G₁(x) имеет следующее построение:

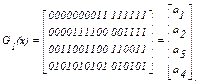
Из данной матрицы видно, что столбцы матрицы представляют собой последовательности чисел, записанных в двоичной системе счисления; младшие разряды (символы) внизу. Следовательно, строки матрицы G_l(x) можно рассматривать как последовательности состояний двоичного суммирующего счетчика, что условно можно представить так:

(3.24)

где 1 – последовательность из одних 1;

S_δl – последовательность состояний последнего (старшего) разряда счетчика;

S_δm – последовательность состояний первого (младшего) разряда счетчика.

Примечание: перестановка столбцов и строк порождающей матрицы приводит к эквивалентным кодам. Строки в порождающих матрицах линейно независимы. Поскольку матрица G₁(x) имеет четыре строки, то матрица G₂(x) будет иметь 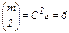строк, которые получаются путем покомпонентного (поэлементного) перемножения строк матрицы G₁(x):

(3.25)

Матрица G₃(x) будет иметь строки, которые также формируются перемножением соответствующих строк G₁(x):

=

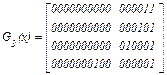Таким образом, порождающая матрица КРМ с Е = 3 и n = 2⁴ = 16 является рангом (15 ´ 16) и вида:

(3.26)

Данная матрица задает (n,k) = (15,16) -код над полем Галуа GF(2): практически это код с проверкой на честность.

Если же принять Е = 2 и m = 4, то можно построить КРМ второго порядка с порождающей матрицей вида:

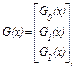(3.27)

которая задает код с параметрами (n,k) = (16,11) над двоичным поле Галуа GF(2); практически это расширенный код Хэмминга с параметрами (n,k)=(15,11).

При Е = 1 и m = 4 можно построить КРМ первого порядка с порождающей матрицей вида:

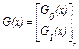(3.28)

которая задает код с параметрами n = 2^m = 2⁴ = 16 двоичных символов, k = 1+ =5, l = n-k = 16-5 = 11, d₀ = 2^m-E = 2^4-1 = 8, т. е. (n,k,d₀) =(16,5,8) -код.

Таким образом, КРМ Е-го порядка получается пополнением или расширением КРМ (Е-1)-го порядка, а КРМ (Е-1)-го порядка получается из кода Е-го порядка, получается выбрасывания символов. Так как КРМ Е-го порядка содержит (Е-1)-го порядка, то его минимальное кодовое расстояние d₀ не может быть больше d₀ КРМ (Е-1)-го порядка и, как отмечалось выше, КРМ Е-го порядка имеет d₀ = 2^m-E. Доказательство этого положения состоит в следующем. Каждая строка матрицы G_i(x) имеет честный вес, а сумма двух двоичных кодовых последовательностей (кодовых векторов) четного веса также имеет четный вес. В этом случае все линейные комбинации строк матрицы G(x) имеют четный вес, а это значит, что все кодовые последовательности имеют четный вес. Матрица G_Е(x) содержит строки весом w_E = 2^m-E и, следовательно, минимальный вес кода не превышает 2^m-E , т. е. w_min ≤ 2^m-E.

КРМ Е-го порядка позволяет исправлять 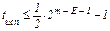ошибочных символов и восстанавливать k информационных символов. Данную корректирующую способность обеспечивает алгоритм декодирования КРМ, предложенный Ридом [3,4]. Алгоритм Рида отличается от большинства алгоритмов декодирования тем, что позволяет восстановить информационные символы прямо из принятой кодовой последовательности. В этом алгоритме декодирования не дается точного значения самой ошибки и не используются промежуточные переменные, например, синдром. Сущность алгоритма декодирования состоит в следующем:

– предположим, что имеется декодер для КРМ (Е-1)-го порядка, исправляющего 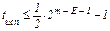ошибочных информационных символов;

– требуется разработать декодер для КРМ Е-го порядка, исправляющего ошибочных символов, сведя это случай к предыдущему;

– так как КРМ нулевого порядка может быть декодирован с использованием мажоритарного алгоритма декодирования, то данный алгоритм декодирования может быть применен к КРМ более высоких порядков.

Для реализации алгоритма декодирования кодирование информации КРМ производится следующим способом:

– передаваемый информационный блок разбивается на (Е+1) сегментов, положив i = [ I₀, I₁,…, I_E ], где сегмент I_i содержит информационных символов;

– каждый информационный сегмент умножается на один блок матрицы G(x). Кодирование можно представить поблочным умножением вектора-строки на матрицу:

(3.29)

– предположим, что информационная последовательность разбита на сегменты следующим образом: каждому информационному сегменту соответствует один из Е блоков порождающей матрицы G(x), который при кодировании умножается на этот сегмент (или наоборот – сегмент на блок).

После принятия кодовой последовательности F'(x) декодер пытается восстановить информационные символы в Е -сегменте и после этого определяет вклад этих символов в принятую кодовую последовательность и вычесть его из принятой кодовой последовательности; далее задача декодирования уже сводится к декодированию КРМ (Е-1)-го порядка. Таким образом, алгоритм декодирования КРМ Е-го порядка представляет собой последовательность мажоритарных алгоритмов декодирования и начинается декодирование с нахождения информационных символов в Е-м сегменте.

Представим принятую кодовую последовательность F'(x) в следующем виде F'(x)=i·G(x)Åi(x), где i(x) – помеха. Далее декодер восстанавливает информационный сегмент I_E, а затем вычисляет разность

(3.30)

которая является искаженной кодовой последовательностью КРМ (Е-1)- го порядка.

Рассмотрим декодирование информационного символа i_k-1, т. е (k-1) -го символа, который умножается на последнюю строку матрицы G_E(x). Декодируется этот символ путем вычисления 2^m-E проверочных уравнений (проверочных сумм) по 2^E символов из 2^m символов принятой кодовой последовательности, так что каждый принятый символ входит только лишь в одно проверочное уравнение (формируется система 2^m-E раздельных проверок), а декодируемый информационный символ i _k-1 входит во все проверки. При отсутствии ошибок все проверки дают значение информационного символа i _k-1, но даже, если имеется не более ошибок более половины проверок будут правильно давать значение информационного символа i _k-1.

Формирование проверок (проверочных сумм) выполняется по следующему правилу:

– первая проверка есть сумма по модулю два первых двух символов принятой кодовой последовательности;

– вторая проверка есть сумма по модулю два вторых 2^E символов принятой кодовой последовательности и т.д.

Всего формируется 2^m-E проверок и по предложению имеется ошибочных символов, а мажоритарное голосование (принятое решение о декодируемом информационном символе по большинству одинаковых результатов сформированных проверок) дает правильное значение i _k-1 символа.

Так для рассмотренного КРМ с параметрами (n,k) = (16,15) эти 2^m-E = 2^4-2 = 4 проверки имеют следующие выражения:

П⁽¹⁰⁾₁=С₀ÅС₁ÅС₂ÅС₃, П⁽¹⁰⁾₃=С₈ÅС₉ÅС₁₀ÅС₁₁,

П⁽¹⁰⁾₂=С₄ÅС₅ÅС₆ÅС₇, П⁽¹⁰⁾₃=С₁₂ÅС₁₃ÅС₁₄ÅС₁₅. (3.31)

Если произошла ошибка только в одном символе, то ошибочной будет также только одна проверка, а мажоритарное голосование по остальным трем проверкам позволяет правильно восстановить информационный символ i⁽¹⁰⁾.

В случае возникновения двух ошибок ни одно значение проверок не встречается чаще других (нет большинства одинаковых результатов решения проверок), что позволяет обнаружить только наличие ошибок в принятой последовательности, в частности – наличие двукратных ошибок.

Аналогичным способом может быть декодирован любой информационный символ, который умножается на одну из строк матрицы G_E(x); это обеспечивается тем, что любая строка матрицы G_E(x) ничем не выделяется среди остальных. Перестановкой столбцов матрицы G_E(x) можно добиться того, что любая строка будет выглядеть также как последняя строка матрицы G_E(x).

Следовательно, можно использовать те же самые проверки, соответственно переставив индексы у символов, входящие в эти проверки. После построения 2^m-E проверок каждый символ будет декодироваться мажоритарным способом. После того, как информационные символы данного сегмента будут определены, их вклад в кодовую последовательность вычитается из принятой кодовой последовательности. Эта процедура эквивалентна построению кодовой последовательности КРМ (Е-1)- го порядка. Последний сегмент информационных символов данного кода определяется также с использованием алгоритма мажоритарного декодирования. Такая процедура декодирования информационных символов продолжается до тех пор, пока не будут декодированы все информационные символы. Таким образом, декодирование КРМ Е-го порядка осуществляется поэтапно от определения информационных символов I_E сегмента до определения информационных символов I₀ нулевого сегмента.

Date: 2015-09-22; view: 914; Нарушение авторских прав