Синтез кодека циклического кода с формированием системы раздельных проверок

Название алгоритма мажоритарного декодирования вытекает из самой сущности реализации алгоритма декодирования, а точнее от способа принятия решения о полярности (знаке) декодируемого информационного символа. При мажоритарном алгоритме декодирования решение о полярности декодируемого информационного символа принимается по большинству одинаковых результатов решения проверочных уравнений (проверок); реализуется принцип «голосования». Это означает, что если более 50% результатов решения проверочных уравнений имеют значения логической «l» или логического «0», то декодер формирует соответственно информационные символы равные «l» или «0». При равном количестве результатов решения проверочных уравнений условно принято, что декодер формирует нулевой информационный символ, т. е. решение принимается в пользу «0».

В разделе 2 отмечалось следующее свойство систематических линейных кодов: если принятую кодовую последовательность F(x) умножить на транспонированную проверочную матрицу кода H^T_l,n(x), то можно получить следующие два результата:

F'(x)∙H^T_l,n(x) = 0,

(3.1)

F'(x)∙H^T_l,n(x) ≠ 0

Результат решения первого уравнения означает, что в принятой кодовой последовательности ошибок нет или ошибки не обнаруживаются кодом. Результат решения второго уравнения противоположен первому.

Так как любой ЦК имеет l проверочных символов, то можно составить 2 ^l проверочных уравнений вида (2.16). В общем виде проверочное уравнение для некоторой j-ой строки транспонированной проверочной матрицы H^T_l,n(x) можно записать так:

.

Используя же свойство цикличности кода, можно построить и все 2 ^l проверочных уравнений, что можно записать так [3,4,6,7]:

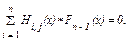
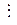(3.2)

.

Главной задачей алгоритма мажоритарного декодирования является выбор или составление «хорошего» или «оптимального» (в плане обеспечения максимальной корректирующей способности кода) подмножества проверочных уравнений; при условии, если оно существует.

Наиболее «просто» составляются проверочные уравнения, в основе которых лежит следующая идея: если декодирующий информационный символ входит во все проверочные уравнения, а остальные символы, входящие в эти проверочные уравнения, входят только по одному разу, данную идею можно записать в виде следующей системы проверочных уравнений относительно некоторого информационного символа, например, a_j:

a_j = k Å m Å γ Å…Å ζ,

(3.3)

a_i = F Å N Å G Å…Å C.

Записанная система проверочных уравнений носит название «системы раздельных проверочных уравнений (проверок)» – СРП. Исходя из вышеизложенного следует: если множество μ (μ ≥ 2) проверочных уравнений (n,k) -кода ортогональны относительно некоторого символа и данный символ входит во все проверочные уравнения, а все остальные символы, входящие в эти проверочные уравнения, входят только в одно проверочное уравнение, то к данному (n,k) -коду возможно применение алгоритма мажоритарного декодирования и при этом будет гарантировано обеспечиваться коррекция ошибок кратностью t_исп ≤ μ/2 двоичных символов.

Таким образом, при требуемой или заданной корректирующей способности кода синтез кодека, реализующий алгоритм мажоритарного декодирования, включает выполнение следующих операций (процедур):

1) определение минимально необходимого количества ортогональных проверочных уравнений, используя равенство μ=2*t_исп+1; последний член данного равенства характеризует, так называемое, тривиальное уравнение относительно декодируемого информационного символа, например, a_i= a'_i;

2) построение проверочной матрицы Н(х) либо в канонической форме, либо в транспонированной форме;

3) формирование по построенной проверочной матрице системы раздельных проверок;

4) разработка структурных, функциональных и принципиальных электрических схем кодека;

5) проверка коррекции кодеком ошибок заданной кратности.

Используя данную методику, выполним синтез кодека циклического кода Хэмминга, реализующего алгоритм мажоритарного декодирования при следующих параметрах кода: (n,k,d₀)=(7,3,4), Р(х)=х⁴+х³+х²+1.

1. Построим проверочную матрицу в канонической форме, для чего находим проверочный полином по формуле

h(x) = (xⁿ+1)/P(x) = (x⁷+1)/(х⁴+х³+х²+1) = х³+х²+1 = 1101.

2. Строим проверочную матрицу H_l,n(х)=Н_4,7(х) по следующему правилу: первый столбец матрицы записываем с использованием проверочного полинома, представленного в двоичной форме и дополним его снизу нулевыми символами до n=7, второй, третий и четвертый столбцы записываем путем последовательного циклического сдвига вниз двоичных символов первого столбца. Построенная поверочная матрица будет иметь следующий вид:

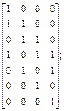H_4,7(x) = (3.4)

3. Определяем необходимое количество ортогональных проверочных уравнений, исходя из корректирующей способности кода, а именно t_исп ≤ (d₀-1)/2=(3-1)/2=1 двоичный символ. Так как код корректирует одиночные ошибки, то достаточно сформировать μ=2∙t_исп+1=2∙1+1=3 проверочных уравнения и дополнительно ввести тривиальное проверочное уравнение. Таким образом, необходимо сформировать четыре проверочных уравнения; μ'=μ+1.

4. Определяем необходимое количество раздельных проверочных подматриц, используя следующее равенство N=μ'-1=4-1=3.

5. Строим подматрицы раздельных проверок, которые обозначим как q_1,1(x), q_2,1(x), q_3,1(x). Первые (левые) столбцы данных подматриц записываются соответственно с использованием трех столбцов проверочной матрицы (3.4). Вторые столбцы данных подматриц записываются путем циклического сдвига вверх на один такт двоичных символов первых столбцов. Двоичные символы третьих столбцов данных подматриц формируются следующим образом:

для первой подматрицы – путем суммирования по модулю два двоичных символов первого, второго и третьего столбцов матрицы (3.4);

для второй подматрицы – путем суммирования по модулю два двоичных символов второго, третьего и четвертого столбцов матрицы (3.4);

для третьей подматрицы – путем суммирования по модулю два двоичных символов первого, второго и четвертого столбцов матрицы (3.4). Таким образом, раздельные проверочные подматрицы будут иметь следующую структуру:

q_1.1 = q_2.1 = q_3.1 = (3.5)

Из построенных раздельных проверочных подматриц видно, что первая, вторая и третья строка соответствующих подматриц состоят из «1», а все остальные строки подматриц содержат по одной «1».

6. По полученным раздельным проверочным подматрицам (3.5) формируем ортогональные проверочные уравнения, дополняя их тривиальными уравнениями. Позиции или номера информационных символов, которые должны участвовать в формировании проверочных уравнений соответственно для информационных символов а₁,а₂,а₃, определяются номерами строк подматриц, которые начинаются с единиц. Таким образом, можно сформировать следующие системы проверочных уравнений для каждого информационного символа:

S₁ = а₁ = а₁ а₂ = а₂ а₃ = а₃

S₂ = а₁Åа₂Åа₄ а₂Åа₃Åа₅ а₃Åа₄Åа₆ (3.6)

S₃ = а₁Åа₃Åа₇ а₂Åа₁Åа₄ а₃Åа₂Åа₅

S₄ = а₁Åа₅Åа₆ а₂Åа₆Åа₇ а₃Åа₁Åа₇.

Сущность способа системы построения раздельных проверочных уравнений с использованием транспонированной проверочной матрицы состоит в следующем:

1) проверочный полином h(x), представленный в двоичной форме записи h(x)=х³+х²+1=1101, записываем в качестве первой строки проверочной матрицы Н_4,7(х) и дополняем строку нулями до n=7 двоичных символов;

2) производим l-1=4-1=3 циклических сдвига двоичных символов первой строки вправо. В результате получаем следующую матрицу:

H_4,7(х) = (3.7)

3) транспонированную проверочную матрицу строим следующим образом.

Первую строку матрицы (3.7) переписываем без изменения. Вторую строку транспонированной проверочной матрицы формируем путем суммирования по модулю два двоичные символы первой, второй и третьей строк матрицы (3.7), а третью строку матрицы формируем путем суммирования по модулю два двоичных символов первой, второй и четвертой строки. В результате получаем следующую транспонированную проверочную матрицу кода

H^T(x) = 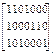(3.8)

Ненулевые символы строк данной матрицы определяют позиции (номера) символов, которые участвуют в формировании системы раздельных проверочных уравнений, а именно: S₁=а'₁, S₂=а₁Åа₂Åа₄, S₃=а₁Åа₃Åа₇, S₄=а₁Åа₅Åа₆. Данная система раздельных проверочных уравнений совпадает с СРП первой проверочной подматрицы (3.5). Для информационных символов а₂ и а₃ СРП формируются (составляются) автоматическим путем циклического сдвига символов СРП S₁…S₄ соответственно на один и два такта, т.е. используется главное свойство циклических кодов – цикл.

По сформированным проверочной матрице (3.4) и подматрицам (3.5) разрабатываем обобщенные структурные и функциональные схемы кодера и декодера (кодека). Процессы кодирования и декодирования помехоустойчивых кодов могут выполняться как в параллельном, так и в последовательном коде. В связи с тем, что в системах связи передача информации производится в последовательном коде, то в разрабатываемых электрических схемах кодера необходимо предусмотреть коммутаторы распределения и объединения информации.

Синтез структурных схем кодека

Для разработки структурных схем кодера и декодера определим их основные функции и требуемые для их реализации функциональные блоки (узлы).

Основные функции кодера:

1) распределение символов входной информации на k (k=3) информационных подпотоков;

2) формирование l=n-k (l=7-3=4) проверочных символов;

3) формирование «n» (n=7) кодовых символов путем объединения «k» (k=3) информационных и «l» (l=4) проверочных символов в единый кодовый поток.

Для реализации данных функций необходимы следующие функциональные блоки:

– КРИ-1/k (КРИ-1/3) – коммутатор распределения информационных символов на три подпотока;

– БСМ – блок сумматоров по модулю два;

– КОИ-n/1 (КОИ-7/1) – коммутатор объединения информации семи параллельных подпотоков в единый поток;

– ФТИиСУ – формирователь тактовых импульсов и сигналов управления кодера.

В соответствии с этим обобщенная структурная схема кодера будет иметь следующее построение (рисунок 3.1).

Кодер работает следующим образом. Входные информационные символы последовательности Q(x) в КРИ-1/3 распределяются на три параллельных подпотока а₁,а₂,а₃ и данные символы поступают одновременно на соответствующие входы КОИ-7/1 и сумматоров по модулю два БСМ. Сформированные проверочные символы а₄,а₅,а₆ и а₇ в параллельном коде поступают на соответствующие входы КОИ-7/1, который формирует кодовую последовательность F(x), кодовые символы которой (F(x)=а₁,а₂,а₃,а₄,а₅,а₆,а₇) в последовательном коде поступают в канал связи (на вход соответствующего модулятора). Для нормального функционирования кодера формируются тактовые частоты f_Т, f_Т1 и сигналы управления с₁,с₂,с₃.

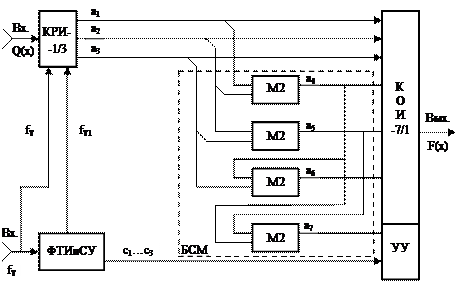
Рисунок 3.1 – Обобщенная структурная схема кодера

Основными функциями декодера являются:

1) запись принятых кодовых символов в последовательный регистр сдвига (RG);

2) формирование системы раздельных проверочных уравнений;

3) формирование информационного символа;

4) выдача информационного символа получателю с одновременной записью данного символа в регистр сдвига.

Для реализации данных функций необходимы следующие функциональные блоки:

– последовательный регистр сдвига на n (n=7) ячеек памяти;

– формирователь системы раздельных проверочных уравнений (ФСРПУ);

– мажоритарный элемент (МЭ);

– коммутатор (К);

– ключи управления (Кл.);

– ФТИд – формирователь тактовых импульсов декодера.

В соответствии с этим обобщенная структурная схема декодера будет иметь следующее построение (рисунок 3.2).

Декодер работает следующим образом. В первоначальный момент времени ключ (Кл.1) открыт (стрелка вниз), а второй ключ (Кл.2) закрыт (стрелка вверх) и принятые кодовые символы последовательности F'(x) записываются в последовательный регистр сдвига.

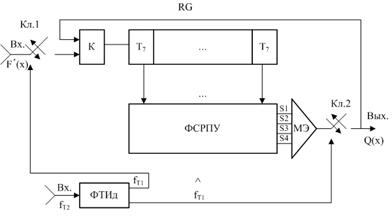
Рисунок 3.2 – Обобщенная структурная схема декодера

Одновременно с записью кодовых символов производится формирование проверочных уравнений в соответствии с равенствами первой подматрицы. По окончании n=7 -го такта положение ключей меняется на обратное: ключ Кл.1 закрывается (стрелка вверх), а Кл.2 открывается (стрелка вниз). На n+1=7+1=8 такте мажоритарным элементом формируется и выдается первый информационный символ а₁, который поступает к получателю информации и по цепи обратной связи через коммутатор (К) на вход последовательного регистра сдвига. По окончании n+2=7+2=9 такта формируется и выдается второй информационный символ а₂, а n+3=7+3=10 тактом – третий информационный символ а₃; после этого положение ключей Кл.1 и Кл.2 меняется на обратное и производится запись и декодирование следующей кодовой последовательности и т.д.

Синтез функциональных схем кодека

Основная задача при разработке функциональных схем кодека состоит в выборе способов построения функциональных блоков кодека, обеспечивающих минимальную сложность разработки и реализации принципиальных электрических схем кодека. В общем, выбор способов построения функциональных схем кодека зависит от опыта и квалификации разработчика систем связи и обработки информации. Далее рассмотрим один из способов (вариантов) построения функциональных схем разрабатываемого кодека.

В кодере, в соответствии с обобщенной структурной схемой, основными функциональными блоками являются: входной коммутатор распределения информации КРИ-1/3, выходной коммутатор объединения информации КОИ-7/1, формирователь проверочных символов, формирователь тактовых импульсов ФТИ и формирователь сигналов управления ФСУ. Формирователь тактовых импульсов синхронизирует работу узлов КРИ и формирователя проверочных символов, а ФСУ обеспечивает логику работы КОИ.

КРИ-1/3 может быть выполнен в виде двух регистров сдвига: последовательного регистра сдвига (RG1) и параллельного регистра сдвига (RG2). Каждый из регистров сдвига содержит «k» ячеек памяти (k=3). Запись и считывание информации осуществляется тактовыми частотами соответственно f_Т и f_Т1, поступающие от ФТИк и выполняемого в виде делителя частоты на три. Функциональная схема КРИ-1/3 приведена на рисунке 3.3. Формирователь проверочных символов (а₄…а₇) выполняется в виде блока сумматоров по модулю два, реализуемых с помощью двухвходовых схем «Исключающее ИЛИ».

Так как информационные и проверочные символы образуют синфазные и синхронные потоки, то для их объединения в единый кодовый поток можно использовать синхронный мультиплексор с соответствующим количеством информационных и управляющих входов.

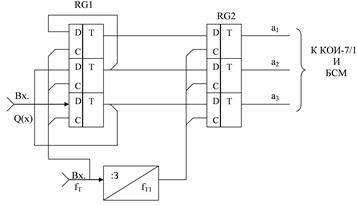
Рисунок 3.3. Функциональная схема КРИ-1/3

Сигналы управления символов синхронных потоков мультиплексора поступают от формирователя сигналов управления, выполняемого в виде кольцевого счетчика на семь. Функциональная схема КОИ-7/1 приведена на рисунке 3.4. Кольцевой счетчик на семь выполняется в виде двоичного счетчика (Дв.сч.) и дешифратора (ДШ). Обобщенная функциональная схема кодера приведена на рисунке 3.5.

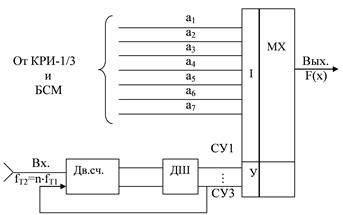
Рисунок 3.4 – Функциональная схема КОИ-7/1 кодера

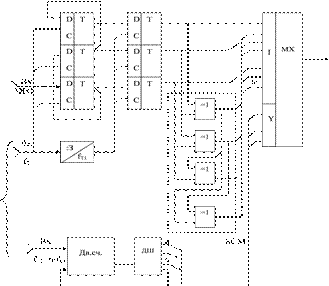
Рисунок 3.5 – Обобщенная функциональная схема кодера

В декодере, в соответствии с обобщенной структурной схемой (рисунок 3.2), основными функциональными блоками являются: последовательный регистр сдвига (RG), ФСРПУ, коммутатор (К), ФТИд, ключи управления (Кл.1 и Кл.2) и мажоритарный элемент (МЭ).

Последовательный регистр сдвига выполняется в виде n (n=7) ячеек памяти (D-триггеров). ФСРПУ выполняется в виде совокупности сумматоров по модулю два, которые могут быть реализованы на основе двухвходовых схем «Исключающее ИЛИ». Мажоритарный элемент может быть выполнен различными способами. Критериями выбора построения МЭ являются обеспечение высокого быстродействия и минимального объема оборудования. При количестве проверочных уравнений менее 10 (μ<10) МЭ целесообразно выполнять в виде комбинационного автомата (КА), имеющего μ входов и один выход.

При μ>10 МЭ целесообразно выполнять в виде двоичного счетчика с соответствующим дешифратором. ФТИд целесообразно выполнять по принципу построения ФТИк, что будет обеспечивать технологичность производства кодека. Обобщенная функциональная схема декодера приведена на рисунке 3.6.

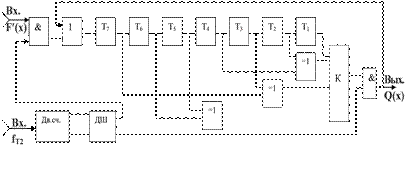
Рисунок 3.6 – Обобщенная функциональная схема декодера

Коррекция ошибок допустимой кратности (t_исп.= 1 двоичный символ) разработанным кодеком выполняется следующим образом. Пусть на вход кодера поступил информационный блок Q(x) следующего вида: а₁=а₂=а₃=0, т. е. Q(x) = 000. Следовательно, проверочные символы а₄,а₅,а₆ и а₇ также будут нулевыми, т. е. а₄а₅а₆а₇=0000. Сформированная кодовая последовательность также будет нулевой, т. е. F(x) = а₇а₆а₅а₄а₃а₂а₁ = 0000000. Пусть при передаче по каналу связи F(x) будет искажен первый информационный символ а₁, т. е. а₁=1. Следовательно, принятая кодовая последовательность F'(x) будет иметь F'(x) = 0000001.

Декодер, в соответствии с формулами (3.6), формирует следующие результаты проверочных уравнений:

S₁= а'₁ = 1; S₃ = а₃Åа₇ = 0Å0 = 0;

S₂= а₂Åа₄ = 0Å0 = 0; S₄ = а₅Åа₆ = 0Å0 = 0.

В этом случае на входы КА декодера поступит комбинация двоичных символов вида 1000 и КА по большинству одинаковых (нулевых) результатов решения проверочных уравнений сформирует выходной информационный символ а₁ с уровнем логического нуля, т. е. а₁=0 и, следовательно, принятый ошибочный информационный символ будет исправлен. Можно показать и доказать, что данный декодер обладает способностью корректировать двукратные ошибки структуры â₂â₁, т. е. F(x) = а₇а₆а₅а₄а₃â₂â₁ = 0000011.

Date: 2015-09-22; view: 809; Нарушение авторских прав