Синтез функциональных схем кодека, реализующего мажоритарный алгоритм декодирования кодов Рида-Маллера

Синтез функциональных схем кодека выполним для КРМ первого порядка с параметрами: n = 8 двоичных символов, m = log₂8 = 3, Е = 1, d=2^m-E=2^3-1=4 и 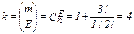двоичных символа.

Порождающая матрица данного КРМ имеет следующее построение

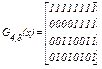
Кодирование информации КРМ осуществляется путем умножения исходного информационного сообщения Q(x) = а₀а₁а₂а₃ на матрицу, т. е. по правилу F(x) = Q(x)·G_4,8(x)=δ₀δ₁δ₂δ₃δ₄δ₅δ₆δ₇. В этом случае формируются кодовые последовательности неразделимого кода, которые содержат по n = 8 двоичных символов. Процесс кодирования (формирование кодовых последовательностей) может быть реализован с использованием как сумматоров по модулю два, так и двоичного счетчика. Принимаем вариант построения кодека КРМ с использованием сумматоров по модулю два для чего составим уравнения формирования кодовых символов (δ₀δ₁δ₂δ₃δ₄δ₅δ₆δ₇), которые имеют следующий вид: ,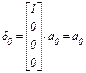

δ₁ = а₀Åа₁, δ₂ = а₀Åа₂, δ₃ = а₀Åа₁Åа₂, δ₄ = а₀Åа₃, δ₅ = а₀Åа₁Åа₃ = δ₁Åа₃, δ₆ = а₀Åа₂Åа₃ = δ₂Åа₃, δ₇ = а₀Åа₁Åа₂Åа₃ = δ₃Åа₃.

В соответствии с данными уравнениями обобщенная функциональная схема кодера кода Рида-Маллера с параметрами (n,k,d₀)=(8,4,4), будет иметь следующее построение (рисунок 3.19). Принцип работы кодера аналогичен принципу работы кодера ЦК, функциональная схеме которого приведена на рисунке 3.10.

Рисунок 3.19 – Обобщенная функциональная схема кодера кода

Рида-Маллера первого порядка (n,k,d₀)=(8,4,4)

Кодер формирует кодовые последовательности несистематического кода. Путем перестановки столбцов и суммирования строк можно сформировать каноническую порождающую матрицу КРМ и кодер будет формировать кодовые последовательности разделимого кода.

Для синтеза функциональной схемы декодера КРМ, реализующего мажоритарный алгоритм декодирования, необходимо сформировать систему раздельных проверочных уровней (проверок). Система раздельных проверок формируется на основе порождающей матрицы G_4,8(x) и имеет следующую структуру:

а₁ = δ₀Åδ₁, а₂ = δ₀Åδ₂, а₃ = δ₀Åδ₄,

а₁ = δ₂Åδ₃, а₂ = δ₁Åδ₃, а₃ = δ₁Åδ₅,

а₁ = δ₄Åδ₅, а₂ = δ₄Åδ₆, а₃ = δ₂Åδ₆,

а₁ = δ₆Åδ₇, а₂ = δ₅Åδ₇, а₃ = δ₃Åδ₇.

Для определения а₀ необходимо знать значения а₁,а₂,а₃, а также результат решения уравнения истинности, т. е. а₀=δ₀. В соответствии с данной системой раздельных уравнений обобщенная функциональная схема декодера КРМ будет иметь следующее построение (рисунок 3.20). Выполним оценку корректирующей способности разработанного кодека КРМ, используя для этого сформированные системы проверочных уравнений. Предположим, что на вход кодера КРМ (рисунок 3.19) поступило информационное сообщение Q(x), состоящее из нулевых двоичных символов, т. е. Q(x) = а₀а₁а₂а₃ = 0000. Кодер в этом случае, сформирует кодовую последовательность F(x), состоящую также из одних нулевых двоичных символов, т. е. F(x) = δ₇δ₆δ₅δ₄δ₃δ₂δ₁δ₀ = 00000000. Пусть при передаче по каналу связи искажению подвергались два первых кодовых символа, т. е. F'(x) = 00000011.

В декодере КРМ (рисунок 3.20), в соответствии с уравнениями порождающей матрицы G_4,8(x), будут сформированы следующие значения информационных символов (пороги срабатывания всех мажоритарных элементов (МЭ₁…МЭ₄) декодера устанавливаются равными , μ – количество проверочных уравнений).

Система проверочных уравнений для первого информационного символа имеет следующий вид:

Сформированные с помощью этой системы символы поступают на входы МЭ₂, который сформирует значение a₁=0, т. е. ошибка будет исправлена.

Система проверочных уравнений для второго информационного символа имеет вид:

Сформированные с помощью этой системы символы поступают на входы МЭ₃, который сформирует значение a₂=0,

Система проверочных уравнений для третьего информационного символа имеет:

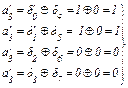
Сформированные с помощью этой системы символы поступают на входы МЭ₄, который сформирует значение a₃=0.

Рисунок 3.20 – Обобщенная функциональная схема декодера кода Рида-Маллера первого порядка с (n,k,d₀) = (8,4,4)

Сформированные информационные символы а₁=0, а₂=0 и а₃=0 одновременно поступают на соответствующие входы КОИ-4/1, выполняемого в виде синхронного мультиплексора, и на входы мажоритарного элемента МЭ₁, на один из входов которого поступает кодовый символ δ'₀ = 1. Так как большинство одинаковых результатов решений проверочных уравнений соответствует ненулевым символам, то МЭ₁ сформирует значение а₀ = 0. Таким образом, декодер КРМ выполнил коррекцию двух ошибочных информационных символов. КОИ-4/1 декодера преобразует передачу из параллельного кода в последовательный код сообщения Q(x).

Date: 2015-09-22; view: 1137; Нарушение авторских прав