Синтез кодека циклического кода, реализующего синдромный алгоритм декодирования

В соответствии с [1-4,6,8,9] достоинствами синдромного алгоритма декодирования являются простота алгоритмов кодирования и декодирования и высокая скорость обработки информации (отсутствие задержки информации при декодировании).

Во втором разделе данного пособия было установлено, что синдром представляет собой двоичный вектор S(х) длины l символов, который может быть получен различными способами. Например, как произведение принятой кодовой последовательности F'(x) на транспонированную проверочную матрицу H_l,n^Т(х), т. е. S(x) = F'(x)∙H_l,n^Т(х), или как результат деления F'(x) на образующий полином Р(х), т. е. S(x) = R(x) = F'(x)/Р(х). Структура синдрома S(x) зависит лишь от количества и структуры ошибок в принятой кодовой последовательности F'(x).

В случае использования полиномиальных кодов синдромный вектор (синдром) чаще всего сопоставляется со структурой проверочной матрицы H_l,n(х). Характерной особенностью проверочной матрицы линейных кодов является то, что ее столбцы представляют собой любые различные ненулевые комбинации или кодовые слова длиной l двоичных символов. Для линейного кода с параметрами (n,k,d₀) можно построить 2^n-k-1=2^l-1 различных по структуре проверочных матриц.

Проверочные матрицы могут быть построены с использованием как порождающей матрицы G_k,n(x), так и проверочного полинома h(x). Кроме того, проверочную матрицу можно построить следующим способом: столбцы проверочной матрицы H_l,n(х) можно представить в виде полиномов от оператора «х» степени (l-1), причем единичному элементу (логической единице) столбца, принадлежащему первой нижней строке матрицы H_l,n(х), соответствует член полинома «х⁰», а единичному элементу последней верхней строки матрицы соответствует член полинома «х^l-1». Следовательно, все столбцы проверочной матрицы H_l,n(х) могут быть получены как остатки от деления хⁱ на образующий полином Р(х), где i – номер двоичного символа (разряда) кодовой последовательности или номер столбца проверочной матрицы минус единица, т. е. 0 ≤i ≤ (n-1). Например, для ЦК Хэмминга с параметрами кода (n,k,d₀)=(15,11,4) проверочная матрица, как один из возможных вариантов, имеет следующую структуру.

Первые «k» столбцов проверочной матрицы определяют информационные символы (а₁…а₁₁), которые входят во все проверочные уравнения, а l = n-k столбцов образуют единичную подматрицу (а₁₂…а₁₅).

Кодовая последовательность F'(х) будет принадлежать (n,k,d₀)- коду, если F'(х)∙H_l,n^Т(х)=0. Следовательно, для реализации синдромного алгоритма декодирования необходимо «связать» полученную структуру синдрома S_i(x) со структурой столбцов проверочной матрицы H_l,n(х), принадлежащих информационным символам, т.е.

Таким образом, позиция столбца проверочной матрицы H_l,n(х), совпадающая со структурой синдромного вектора S_i(x), определяет позицию ошибочного информационного символа, а соответствующий дешифратор декодера, настроенный на данную структуру синдрома, сформирует и выдаст сигнал коррекции.

С целью упрощения рассмотрения способа построения и функционирования кодека, реализующего синдромный алгоритм декодирования, выбираем ЦК Хэмминга с параметрами (n,k,d₀)=(7,4,3) и один из вариантов проверочной матрицы кода следующего вида

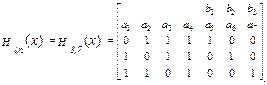(3.14)

Для синтеза структурных схем кодека необходимо установить основные функции, выполняемые соответственно кодером и декодером.

Основными функциями кодера являются:

1) преобразование входной информации Q(x) из последовательного кода в параллельный код;

2) формирование проверочных символов;

3) формирование кодовой последовательности F(x) путем последовательного объединения «k» информационных символов и l=n-k проверочных символов в единый кодовый поток.

Для реализации данных функций в кодере необходимы следующие функциональные блоки:

– КРИ-1/k (КРИ-1/4) – коммутатор распределения входной информации на «k» (k = 4) подпотоков;

– ФПС_к – формирователь проверочных символов кодера;

– КОИ – n/1 (КОИ-7/1) – коммутатор объединения информации «n» (n=7) параллельных подпотоков в единый поток;

– ФСУ_к – формирователь сигналов управления КРИ-1/4 и КОИ-7/1 кодера.

В соответствии с перечисленными выше функциями обобщенная структурная схема кодера будет иметь следующее построение (рисунок 3.8).

Рисунок 3.8 – Обобщенная структурная схема кодера с синдромным алгоритмом декодирования

В кодере, в соответствии с проверочной матрицей (3.14), ФПС_к формирует проверочные символы b₁b₂b₃, которые поступают на соответствующие входы КОИ-7/1 и далее передаются вслед за информационными символами в канал связи, образуя тем самым кодовую последовательность F(x).

Основными функциями декодера являются:

1) преобразование кодовой последовательности F'(x) из последовательного кода в параллельный код;

2) формирование проверочных символов (b'₁,b'₂,b'₃) из принятых информационных символов а'₁…а'₄ в соответствии с матрицей (3.14);

3) формирование символов синдромной последовательности (синдрома) S₁…S₄;

4) дешифрация (анализ) синдрома и принятие решения о достоверности принятых информационных символов;

5) преобразование информационных символов из параллельного кода в последовательный код и выдача информационного блока символов θ(х) получателю.

Для реализации данных функций в декодере необходимы следующие функциональные блоки:

– КРИ-1/n (КРИ-1/7) – коммутатор распределения информации на «n» (n=7) параллельных подпотоков;

– КОИ-k/1 (КОИ-4/1) – коммутатор объединения информации k (k=4) параллельных подпотоков в последовательный поток;

– ФПС_д – формирователь проверочных символов декодера;

– ФСС – формирователь синдромных символов;

– АС – анализатор (дешифратор) синдрома;

– ФСУ_д – формирователь сигналов управления (КРИ-1/7) и (КОИ-4/1) декодера.

В соответствии с этим обобщенная структурная схема декодера, реализующего синдромный алгоритм декодирования, будет иметь следующее построение (рисунок 3.9).

Декодер работает следующим образом. Входные символы принятой кодовой последовательности F'(x) в КРИ-1/7 распределяются на семь параллельных подпотоков. Информационные символы а'₁…а'₄ одновременно поступают на соответствующие входы КО и ФПС_д. ФПС_д формирует проверочные символы b₁…b₃ из принятых информационных символов в соответствии с проверочной матрицей (3.14). Сформированные проверочные символы поступают на соответствующие входы ФСС, на другие входы которого поступают принятые проверочные символы b'₁…b'₃. Синдромные символы S₁,S₂,S₃, формируются по правилу: S₁=b₁Åb'₁; S₂=b₂Åb'₂, S₃=b₃Åb'₃. Следовательно, синдромный вектор или синдром S_ί(x) в данном случае будет содержать три двоичных символа, т. е. S(x) = S₁,S₂,S₃.

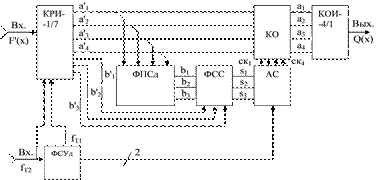
Рисунок 3.9 – Обобщенная структурная схема декодера, реализующего синдромный алгоритм декодирования

При отсутствии ошибок в принятой кодовой последовательности F'(х) синдром будет нулевым, т. е. S(x) = S₁,S₂,S₃ = 000. При наличии ошибок синдром будет ненулевым и его структура будет зависеть от количества ошибок и их позиций в кодовой последовательности F'(х). Так как рассматриваемый ЦК Хэмминга исправляет одиночные ошибки, то условно можно принять следующее: ошибочным информационным символам а'₁…а'₄ структура синдрома S_i(x) соответствует структуре столбцов проверочной матрицы (3.14), т. е. Sа₁(х) = 011 соответствует ошибочно принятому символу а₁, Sа₂(х) = 101 – ошибочному а₂, Sа₃(х) = 110 – ошибочному а₃ и Sа₄(х) = 111 – ошибочному а₄.

Сформированные символы синдрома S_i(x) поступают на соответствующие входы АС, который формирует четыре сигнала коррекции СК₁…СК₄, поступающие на соответствующие входы КО. Условно можно принять, что СК₁ соответствует коррекции информационного символа а₁, СК₂ – символу а₂ и т. д. После соответствующей коррекции информационные символы поступают на соответствующие входы КОИ-4/1, где преобразуются из параллельного кода в последовательный код, и в виде информационного блока Q(x) выдаются получателю.

Синтез функциональных схем кодека, реализующего синдромный алгоритм декодирования ЦК, выполняем по методике, рассмотренной при синтезе функциональных схем кодека ЦК, реализующего мажоритарный алгоритм декодирования.

Синтез функциональной схемы кодера

Из алгоритма работы кодера следует, что принципы построения его функциональных блоков могут быть приняты аналогичными принципами построения функциональных блоков кодера с мажоритарным алгоритмом декодирования, а именно:

– КРИ-1/4 – выполняется в виде последовательного (RG₁) и параллельного (RG₂) регистра сдвига;

– КОИ-7/1 – выполняется в виде синхронного мультиплексора;

– ФПС_к – выполняется в виде совокупности сумматора по модулю два, входы которых подключаются к информационным цепям в соответствии с проверочной матрицей (3.14);

– ФСУ_к – состоит из делителя частоты на четыре и кольцевого счетчика на семь, выполняемого в виде двоичного счетчика и дешифратора.

Функциональная схема кодера приведена на рисунке 3.10

Рисунок 3.10 – Функциональная схема кодера с синдромным алгоритмом кодирования

Синтез функциональной схемы декодера выполняем по следующей методике: блоки декодера, реализующие одинаковые функции с блоками кодера, выполняем по аналогичным принципам их построения. Такими блоками декодера являются: КРИ-1/4, КОИ-1/4, ФПС_д, ФСУ_д.

ФСС и КО выполняются в виде совокупности сумматоров по модулю два;

АС выполняется в виде четырех дешифраторов (ДШ1…ДШ4), настраиваемые соответственно на комбинации синдрома: 011(ДШ1); 101(ДШ2); 110(ДШ3); 111(ДШ4).

Функциональная схема декодера, реализующего синдромный алгоритм декодирования приведена на рисунке 3.11.

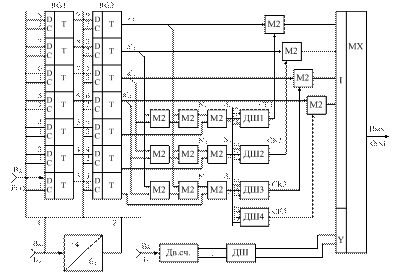
Рисунок 3.11 – Функциональная схема декодера, реализующего синдромный алгоритм декодирования

Корректирующую способность разработанного кодека проверим при следующих условиях:

– информационный блок символов Q(x), поступающих на вход кодера, представляет собой нулевую последовательность, т. е. Q(x) = а₄а₃а₂а₁ = 0000000. Следовательно, сформированная кодовая последовательность F(x) также будет нулевой последовательностью, т. е. F(x) = b₃b₂b₁ а₄а₃а₂а₁ = 0000000;

– при передаче по каналу связи искажен только первый информационный символ а₁, т. е. принята кодовая последовательность следующей структуры F'(x) = b'₃b'₂b'₁а'₄а'₃а'₂а'₁ = 0000001;

ДШ1 настроен на синдром S(x) = 011.

В декодере из принятых информационных символов а'₄а'₃а'₂а'₁ = 0001, в соответствии с проверочной матрицей (3.14), формируются поверочные символы b'₁ = а'₂Åа'₃Åа'₄ = 0Å0Å0 = 0, b'₂ = а'₁Åа'₃Åа'₄ = 1Å0Å0 = 1, b'₃ = а'₁Åа'₂Åа'₄ = 1Å0Å0 = 1. Соответственно синдромные символы будут равны: S₁ = b₁Åb'₁ = 0Å0 = 0; S₂ = b₂Åb'₂ = 0Å1 = 1, S₃ = b₃Åb'₃ = ·0Å1 = 1.

Следовательно, синдром будет иметь следующую структуру: S(x) = 011. Данные символы синдрома одновременно поступают на входы четырех дешифраторов, но только на выходе ДШ1 будет сформирован сигнал коррекции (СК1) с уровнем логической единицы. Данный сигнал коррекции поступит на один из входов сумматора по модулю два первой информационной цепи, а на второй вход сумматора по модулю два поступит ошибочный информационный символ а'₁. В результате суммирования по модулю два ошибочный информационный символ будет исправлен: а'₁ÅСК1=1Å1=0. Аналогичным образом будет производится декодирование последующих кодовых последовательностей.

3.3 Коды Файра: основные свойства, определение, способы кодирования и декодирования, синтез функциональных схем кодека

Коды Файра являются дальнейшим развитием двоичных линейных кодов Абрамсона, которые задаются следующим образующим полиномом вида P(x)=ρ(х)(х+1), где ρ(х) – примитивный полином степени ε, величина которой выбирается равной кратности корректируемых ошибок. Длина «n» кодовых последовательностей кодов Абрамсона определяется выражением n=2^ε-1 двоичных символов, число «k» информационных символов на длине «n» кодовых символов равно k = n-ε-1, а число l=ε+1. Минимальное кодовое расстояние данных кодов равно четырем (d₀=4); данные коды исправляют все одиночные и смежные ошибки [1-8,9].

Циклическим кодом Файра, корректирующего одиночные пакеты ошибок кратностью t_п.исп двоичных символов, называется линейный блоковый код над GF(2), задаваемый образующим полиномом вида

P(x) = ρ(х)(х^с+1), (3.15)

где ρ(х) – примитивный полином над GF(2), степень ε которого не меньше кратности корректирующего пакета ошибок (ε≥ t_п.исп) и который не делит двучлен на (х^с+1);

с ≥ 2·t_п.исп или с ≥ t_п.исп+ t_п.обн-1 – максимальная степень двучлена; t_п.исп и t_п.обн – кратности соответственно исправляемого и обнаруживаемого пакетов ошибок.

Коды Файра обеспечивают одновременно коррекцию одиночных пакетов ошибок кратностью t_п.исп двоичных символов и обнаружение одиночных пакетов ошибок кратностью t_п.обн двоичных символов при условии, что t_п.исп ≤ ε и t_п.исп+t_п.обн-1 ≤ с. Положение пакетов ошибок в кодовой последовательности F_i(x) может быть произвольным, т.е. занимать любые позиции кодовых символов. Если применить перемежение кодовых символов, корректирующая способность кодов Файра к пакетным ошибкам существенно увеличивается.

Двучлен (х^с+1) определяет правило формирования проверок на честность, именно «с» перемежающихся и равномерно расположенных проверок. Так как информационные символы, входящие в каждую проверку, располагаются на расстоянии «с» друг от друга, то при возникновении пакета ошибок кратностью t_п.исп двоичных символов будет искажаться не более одного символа в любой из проверок, а в (с-t_п.исп) последовательных проверках не будет искаженных символов. Поэтому представляется возможным определить, какой по достоверности информационный символ находится в начале пакета ошибок. Дополнительная информация, определяющая положение пакета ошибок, обеспечивается полиномом ρ(х).

К достоинствам ЦК Файра следует отнести сравнительно простые алгоритмы (правила) кодирования и декодирования данных кодов, а также минимальная сложность как аппаратурной, так и программной реализации кодеков. Далее выполним синтез функциональных схем кодека ЦК Файра, используя параметры кода Файра из примера (3.7), а именно: (n,k,d₀) = (42,33,8) = Р(х)=х⁹+х⁷+х⁶+х³+х+1, t_п.исп≤3 двоичных символа и t_п.обн-1 ≤ 4 двоичных символа.

Синтез функциональной схемы кодера. Так как формирование кодовой последовательности F(x) при использовании кода Файра осуществляется
по правилу 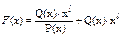, то кодер будет содержать регистр сдвига со встроенными сумматорами по модулю два с обратной связью. Регистр сдвига содержит l=9 ячеек памяти, пять сумматоров по модулю два (на единицу меньше количества ненулевых членов образующего полинома), двухвходовой коммутатор (двухвходовая схема ИЛИ), три ключа управления кодером (двухвходовые схемы И) и формирователь сигналов управления ключами. В соответствии с этим обобщенная функциональная схема кодера ЦК Файра будет иметь следующее построение (рисунок 3.12)

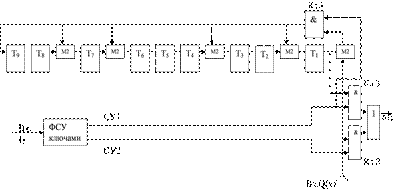
Рисунок 3.12 – Обобщенная функциональная схема кодера ЦК Файра: (n,k,d₀) = (42,33,8) = Р(х)=х⁹+х⁷+х⁶+х³+х+1

На рисунке 3.13 приведены временные диаграммы, поясняющие принцип работы кодера.

Рисунок 3.13 – Временные диаграммы сигналов управления ключами кодера

Синтез функциональной схемы декодера. Сложность разработки функциональной схемы декодера ЦК Файра зависит от используемого алгоритма декодирования. Принимаем, что критериями при выборе алгоритма декодирования являются: обеспечение минимальной задержки информации при декодировании и минимальная сложность реализации декодера. Такими достоинствами обладает конвейерный декодер Меггитта и декодер, построенный на основе образующего полинома, представленного в виде произведения нескольких полиномов. Недостатком последнего декодера является большой объем оборудования. В связи с этим разрабатываем функциональную схему декодера ЦК Файра по схеме Меггитта.

В соответсвии с [1] конвейерный декодер Меггитта содержит следующие функциональные блоки: три генератора синдрома (RG1…RG3), выполняемых в виде последовательных регистров сдвига, первые два из которых имеют встроенные сумматоры по модулю два и обратные связи, а третий регистр сдвига выполняется без сумматоров по модулю два и обратной связи; два буферных устройства (БУ); ключи управления; блок формирования сигналов управления ключами; два дешифратора (ДШ), один из которых осуществляет проверку на наличие не более одной единицы в первом генераторе синдрома, а второй осуществляет проверку на все нули во втором генераторе синдрома и два пороговых элемента. Обобщенная функциональная схема декодера ЦК Файра приведена на рисунке 3.14, а на рисунке 3.15 приведены временные диаграммы, поясняющие принцип работы декодера.

Декодер функционирует следующим образом. В течение 42 тактов ключ Кл.1 открыт, а остальные ключи закрыты, обеспечивая таким образом одновременно запись кодовых символов принятой кодовой последовательности F'(х) в буферное устройство БУ и формирование синдромных символов (). Синдромные символы фиксируются регистром сдвига (RG₁) первого генератора синдрома.

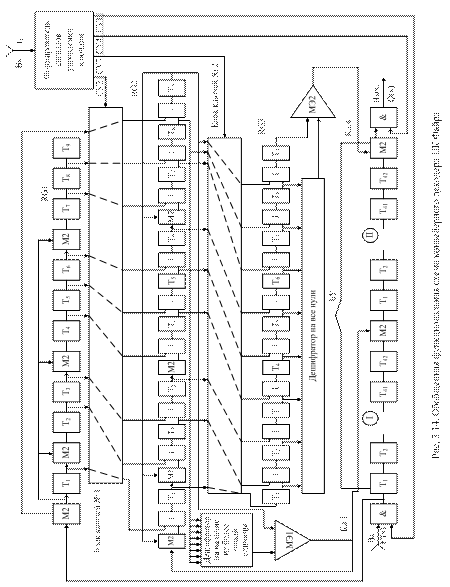
Рисунок 3.14 – Обобщенная функциональная схема конвейерного декодера ЦК Файра

Рисунок 3.15 – Временные диаграммы сигналов управления ключами декодера

По окончании 42 такта синдромные символы из RG₁ записываются в параллельном коде в регистр сдвига RG₂ второго генератора синдрома.

Затем в течение 42 тактов осуществляется одновременно анализ структуры синдромных символов RG₂ («вылавливание» первой ошибки) и коррекция ошибочного информационного символа при перезаписи кодовых символов во вторую часть БУ. По окончании 2∙n = 2∙42=84 такта содержимое регистра (RG₂) переписывается в регистр сдвига RG₃ третьего генератора синдрома и далее в течение к = 33-х тактов осуществляется выдача информации получателю с одновременной коррекцией второй ошибки или второго ошибочного информационного символа. Запись кодовых символов следующей кодовой последовательности осуществляется после окончания 2∙n=2∙42=84 такта декодирования.

3.4 БЧХ-коды: определение, матричное представление, способы кодирования и декодирования, синтез структурных схем кодека

Коды Боузе-Чоудхури-Хоквингема (БЧХ-коды) являются дальнейшим развитием линейных блоковых кодов Хэмминга, относятся к классу циклических кодов и обеспечивают коррекцию как независимых, так и группирующихся (пакетных) ошибок.

В соответствии с [1-5] циклический код длины n=2^ε-1 двоичных символов называется примитивным БЧХ-кодом с конструктивным кодовым расстоянием d=2∙t+1, если его образующий полином равен P(x)=НОК[m₁(x), m₃(x),…m_2t-1(x)], где m_i(x) – минимальный примитивный полином степени ε = log₂(n+1). Максимальная степень Р(х) и, следовательно, число проверочных символов не более l < ε∙t_исп двоичных символов (t_исп – кратность исправляемых ошибок), а число информационных символов равно k = n-ε∙t_исп двоичных символов.

Из определения БЧХ-кода следует, что корнями Р(х) являются элементы α,α³,α⁵,…,α^{2∙tисп-1}, а также α²,α⁴,α⁶,…,α^{2∙tисп .}, т. е. 2∙t_исп последовательных степеней α. Поэтому конструктивное кодовое расстояние кода равно d₀=2∙t_исп+1. Так, например, для БЧХ-кода корректирующего двукратные ошибки (t_исп=2), корнями образующего полинома Р(х) являются элементы α¹,α³, а также α²,α⁴ и d₀=2∙t_исп.+1=2∙2+1=5. Образующий полином Р(х) для данного БЧХ-кода равен Р(х) = m₁(x)∙m₃(x), где m₁(x) и m₃(x) – минимальные полиномы соответственно элементов α¹,α³. Проверочная матрица данного кода имеет вид

(3.16)

Учитывая основное свойство линейных кодов F(x)∙H^Т(х)=0 или Н(х)∙F'(x)=0 следует, что элементы α¹,α³ являются корнями F(x), т.е. F'(α¹)=F(α³)=0.

Для коррекции ошибок произвольной кратности (t двоичных символов) надо увеличивать кодовое расстояние за счет введения большого числа проверочных символов. Циклический код, у которого корнями образующего полинома Р(х) являются δ-1 последовательных степеней α (Р(α^е) = Р(α^е+1) = Р(α^e+2) =…= Р(α^е+δ-2) = 0, е≥0, δ≥1) имеет кодовое расстояние d₀≥δ. Число δ называется конструктивным кодовым расстоянием и является нижней границей кодового расстояния. Поэтому для коррекции всех конфигураций ошибок кратности t надо выбирать образующий полином Р(х) с 2∙t последовательными корнями. Так как кодовые последовательности F_i(x) цикличного кода делятся без остатка на Р(х), то элементы α,α³,α⁵,…,α^{2∙tисп.-1}, а также α,α²,α⁴,…,α^2∙t, являясь корнями P(x), являются корнями полинома F_i(x).

Для того, чтобы выполнялось основное условие F'_i(x)∙H^Т(х)=0, проверочная матрица БЧХ-кода должна иметь вид [1]:

(3.17)

Откуда следует, что кодовые последовательности БЧХ-кода с конструктивным кодовым расстоянием δ имеют δ-1 последовательных нулевых спектральных коэффициентов. Однако в проверочной матрице (3.17) количество строк примерно в два раза меньше, чем значение δ. Это объясняется особенностями поля характеристики два (2), т. е. GF(2) в котором всегда справедливо равенство спектральных коэффициентов f_2∙i=(f_i)² , и для вычисления коэффициентов с четными номерами не требуется проводить дискретного преобразования Фурье (ДПФ). Таким образом, основным признаком принадлежности произвольной кодовой последовательности F_i(x) БЧХ-коду является наличие δ-1 нулевых коэффициентов его ДПФ и совершенно безразлично, в каком участке спектра выбирается этот нулевой отрезок. Так корнями образующего полинома могут быть взяты элементы: α^е, α^е+1, α^е+δ-2. Если ДПФ дает ненулевые значения коэффициентов на этом участке спектра, то кодовая последовательность F_i(x) не принадлежит БЧХ-коду, и это будет свидетельствовать также о наличии искажений кодовой последовательности.

В случае наличия искажений синдром содержит δ-1 составляющую вида S₁(x) = F'(x)∙H^Т(х) = (S₁,S₂,S₃,…S_2t-1,S_2t), где компоненты S₂=(S₁)², S₄=(S₃)², S₆=(S₃)² и т. д. которые восстановлены по S₁,S₃,S₅ и т. д. Компоненты синдрома в точках, где спектральные коэффициенты кодовых последовательностей равны нулю, зависят от номеров (позиций) искаженных символов. Пусть, например, искажения символов произошли на позициях с номерами, выраженные элементами конечного поля: β₁,β₂,…,β_t. Из проверочной матрицы (3.17) следует, что S₁ – сумма номеров искаженных символов, S₂ – сумма квадратов этих номеров и т. д., S₃ – сумма (2t-1) степеней β.

Известно, что такую структуру имеют последовательности S₁,S₂,S₃,…S_2t, удовлетворяющие рекуррентному уравнению, называемому также тождеством Ньютона или разностным уравнением

S_j+t+σ₁∙S_j+t-1+σ₂×S_j+t-2+ …+ σ_t∙S_j = 0, j= 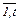, (3.18)

где σ₁,σ₂,…σ_t – коэффициенты полинома локатора ошибок, которые требуется определить. Следует отметить, что коэффициенты ДПФ (S_i, i ≥ 2∙t) принятой кодовой последовательности, т. е. вычисленные за пределами нулевого спектра кода зависят как от вектора ошибки, так и от передаваемой кодовой последовательности, которая неизвестна. Это затрудняет использование коэффициентов S_i для коррекции ошибок. Таким образом, задача коррекции ошибок произвольной кратности БЧХ-кодом с произвольной проверочной матрицей вида (3.17) состоит в решении рекуррентного уравнения вида (3.18).

Алгоритм декодирования двоичных БЧХ-кодов, исправляющих все конфигурации ошибок кратности t (t ≥ 1) двоичных символов, состоит из выполнения трех этапов, а именно [1-4]:

– первый этап декодирования предусматривает вычисление каждого компонента синдрома S_i с нечетным номером путем деления принятой кодовой последовательности F'_i(x) на минимальный полином m_i(x) элемента αⁱ и вычисление значения остатка от деления R_i(х) в точке x = αⁱ: S_i = F'(αⁱ) = R(αⁱ); i -нечетное значение и меньше значения 2∙t. Компоненты синдрома с четными номерами определяются путем возведения в квадрат S_i, так как S_2∙i = (S_i)². (Возведение элемента в квадрат делается по правилам вычисления в конечных полях). Результатом перового этапа является получение последовательности компонентов синдрома S₁,S₂,S₃,…S_2t, которую можно представить полиномом вида S(z) = S₁∙z¹+ ₂∙z²+S₃∙z³+…+S_2tz^2t c коэффициентами из поля GF (2^ε);

– второй этап декодирования предусматривает по полученному синдрому определение полинома локаторов ошибок вида

корни которого z₁ = β₁^-1, z₂ = β₂^-1,…,z _t= β_t^-1 соответствуют обратным номерам искаженных символов.

Основная сложность данного этапа состоит в том, что σ(z) определяется по S(z) неоднозначно. В соответствии с алгоритмом декодирования по максимуму правдоподобия оптимальное решение уравнения состоит в нахождении вектора ошибок минимального веса, т. е. в нахождении полинома локаторов наименьшей степени. Известно несколько способов определения σ(z) по известному синдрому S(z), основанных на решении однородного рекуррентного уравнения (3.18). Доказано, что σ(z) и S(z) удовлетворяют уравнению вида

[1+ S(z)]∙σ(z) = w(z), по mod z^2∙t+1, (3.19)

где w(z) – некоторый полином: при декодировании двоичных БЧХ-кодов определение данного полинома не требуется.

В соответствии с [1-4,5,6,8] уравнение вида (3.19) из-за своего важного и определяющего значения называется ключевым уравнением декодирования. Разработаны многочисленные алгоритмы решения данного уравнения и в частности, основанный на применении алгоритма Эвклида поиска наибольшего общего делителя полиномов S(z) и z^2∙t+1. Таким образом, результатом выполнения второго этапа декодирования является определение полинома локатора ошибок σ(z) наименьшей степени;

– третий этап декодирования включает коррекцию ошибок при условии, что кратность ошибок не превосходит значения t и номера позиций искаженных информационных символов обратны корням полиномов σ(z). Процедура коррекции ошибок заключается в поиске корней полинома σ(z), т. е. в последовательной проверке всех ненулевых элементов поля GF(2^ε) на выполнение равенства σ(αⁱ)=0. В общем случае уравнение σ(x)=0 может выполняться t раз, и соответственно t раз будут формироваться сигналы на коррекцию ошибочных информационных символов. Для синтеза функциональных схем кодека БЧХ-кода необходимо задание образующего полинома Р(х) и алгоритма декодирования. Если алгоритм декодирования кода выбирается исходя из обеспечения минимальной задержки информации при декодировании и сложности реализации декодера, то параметры кода рассчитываются на основании заданной длины n кодовой последовательности и корректируемой кратности t_исп ошибок. Методика расчета параметров БЧХ-кода рассмотрена в разделе 2.2.4.

Используя данные БЧХ-кода примера (2.6) а именно n=15 двоичных символов, t_исп = 2 двоичных символа, k = 7 двоичных символов, d₀ = 5 и Р(х) = х⁸+х⁷+х⁶+х⁴+1, выполним синтез функциональных схем кодера и декодера.

Функциональная схема кодера БЧХ-кода может быть выполнена в виде последовательного регистра сдвига с обратной связью и со встроенными сумматорами по модулю два. На рисунке 3.16 приведена обобщенная функциональная кодера схема БЧХ-кода, реализующая данный принцип построения. Нумерация ячеек памяти принята слева направо.

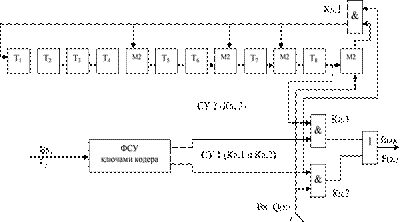
Рисунок 3.16 – Обобщенная функциональная схема кодера БЧХ-кода: (n,k) = (15,7), Р(х) = х⁸+х⁷+х⁶+х⁴+1

Принцип работы кодера аналогичен принципу работы кодера ЦК приведенного на рисунке 3.12.

Сравнительно малая задержка информации при декодировании и сложность реализации декодера БЧХ-кодов обеспечивается при реализации алгоритма вылавливания ошибок. Обобщенная функциональная схема декодера, реализующего алгоритм вылавливания ошибок приведена на рисунке 3.17. На рисунке 3.18 приведены временные диаграммы, поясняющие принцип работы декодера. Декодер содержит следующие основные функциональные блоки: синдромный регистр с дешифратором (ДШ) на все нули, буферное устройство (БУ) с выходным сумматором по модулю два и ключом Кл.2, формирователь сигналов управления ключами (ФСУ Кл.) декодера и ключи управления: Кл.1 – входной ключ, Кл.3 – выходной ключ.

Рисунок 3.17 – Обобщенная функциональная схема декодера БЧХ-кода, реализующая алгоритм вылавливания ошибок: (n,k) = (15,7), Р(х)=х⁸+х⁷+х⁶+х⁴+1

Декодер работает следующим образом. В течение первых 15-ти тактов ключ Кл.1 открыт, а ключи Кл.2 и Кл.3 – закрыты; производится запись кодовых символов в БУ и формирование синдрома. С 16-го по 30-й такт декодирования ключи Кл.1 и Кл.3 закрыты, а ключ Кл.2 – открыт, производится перезапись кодового символа в БУ и коррекция первого ошибочного информационного символа. Затем с 31 такта ключ Кл.3 открывается и в течение семи тактов осуществляется выдача информационного сообщения получателю информации с одновременной коррекцией второй ошибки (второго ошибочного информационного символа). Далее ключи Кл.2 и Кл.3 закрываются, а ключ Кл.1 открывается; производится запись и декодирование аналогичным способом следующей кодовой последовательности.

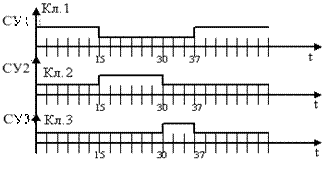
Рисунок 3.18 – Временные диаграммы сигналов управления ключами декодера

3.5 Коды Рида-Маллера: определение, параметры, матричное представление, алгоритмы декодирования и синтез функциональных схем кодеков

Date: 2015-09-22; view: 1866; Нарушение авторских прав