Общие принципы построения укороченных циклических кодов и их свойства

⇐ ПредыдущаяСтр 11 из 22Следующая ⇒

Любой систематический ЦК с параметрами (n,k,d₀) можно укоротить, а именно перейти от кода (n,k,d₀) к коду с параметрами (n-L,k-L,d₀), с выбрасыванием «L» информационных символов (позиций) в каждой кодовой последовательности. Как правило L<k и выбрасываются, т.е. не передаются в канал связи L старших разрядов (символов) кодовой последовательности F(x), которые при укорочении кода полагаются равными «0» и поэтому в канал связи не передаются. Параметр L носит название шага укорочения. При декодировании декодер должен восстановить непередаваемые нулевые символы, так как декодирование осуществляется на полной длине «n» кода.

Если минимальное кодовое расстояние исходного кода равно d₀, то и у укороченного кода оно будет не меньше d₀. Аналогично, если исходный код исправляет пакеты ошибок «t_n» двоичных символов, то укороченный код также исправляет пакеты ошибок длинны «t_n» (или более).

С помощью укорочения и перемежения можно построить большой набор «хороших» кодов, исправляющих пакеты ошибок. Укороченный ЦК уже не является ЦК, а относится к псевдоциклическому коду. Однако укороченный ЦК все-таки обладает алгебраической структурой подмножества соответствующего кольца. В то время как ЦК является идеалом кольца многочленов по модулю хⁿ^-1, то укороченный ЦК является идеалом кольца полиномов по модулю некоторого полинома f(x) степени n'=n-L.

Рассмотрим пример на построение укороченного ЦК. Построение укороченного ЦК можно выполнить с использованием как порождающей матрицы G_k_,_n(x), так и проверочной матрицы H_l_,_n(x).

Пример 2.8. По заданной порождающей матрице ЦК с параметрами (n,k,d₀)=(8,4,4) построить укороченный на L=2 двоичных символа код с параметрами (n'=6, k'=2, d₀'). Определить d₀'.

Решение:

а) пусть задана порождающая матрица вида

G_4,8(х) = (2.10)

б) для построения порождающей матрицы укороченного циклического кода G_k_-_L_,_n_-_L(x)=G_2,6(x) необходимо исключить из матрицы G_4,8(x) две строки которые должны начинаться с ненулевых символов и на старших позициях этих строк должно быть L-2 (допускается L-1) ненулевых двоичных символов, а затем исключить L=2 левых столбца.

В результате получаем следующую порождающую матрицу укороченного кода:

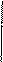
G_4,8(х) = 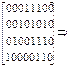G_2,6(х) = 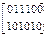; (2.11)

в) определяем d₀' укороченного кода. Так как вес каждой строки равен w_стр=3, а вес проверочной части строки w_пр.стр=2, то, следовательно, укороченный код имеет следующие параметры: (n',k',d₀')=(6,2,3).

Пример 2.9. Построить укороченный ЦК с использованием проверочной матрицы следующего вида:

H_4,8(х) = (2.12)

Решение:

а) принимаем шаг укорачивания кода L=2 двоичных символа;

б) при построении укороченного кода с использованием проверочной матрицы H_l_,_n(x) необходимо исключить из проверочной матрицы L правых столбцов, т.е. в данном примере L=2 столбца;

в) следовательно, исключая из проверочной матрицы (2.12) два правых столбца получаем следующую проверочную матрицу укороченного кода:

H_4,8(х) = 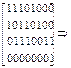H_4,6(х) = (2.13)

2.2.7 Общие принципы построения кодов с использованием процедуры «расширения кода» и их основные свойства

Как уже отмечалось выше, линейные преобразования можно использовать для модификации известных кодов, чтобы сделать их приемлемыми (подходящими) для каких-либо конкретных приложений, а также получения «новых» классов (подклассов) «хороших» кодов.

Любой (n,k,d₀)- код с нечетным минимальным кодовым расстоянием можно расширить до (n+1, k, d₀+1)- кода путем добавления к каждому кодовому слову (кодовой последовательности) суммы всех его двоичных символов в качестве проверки на четность. Это возможно потому, что в случае, когда исходная кодовая последовательность имеет нечетный вес, то к ней будет добавляться единичный символ, т. е. логическая единица. Следовательно, все кодовые последовательности веса d₀ становятся кодовыми последовательностями веса d₀+1. В этом случае, если H(x) – проверочная матрица исходного кода, то расширенный код будет иметь проверочную матрицу вида [1-3,8,9]:

H¢(x) = (2.14)

где 11…1 – строка, состоящая из логических единиц,

– столбец, состоящий из одних логических нулей.

В частности, каждый (2^l-1,2^l-1-l)-код Хэмминга может быть расширен до (2^l,2^l-l)-кода исправляющего одну ошибку (t_исп=1 двоичный символ) и обнаруживающего двукратную ошибку (t_обн=2 двоичных символа). Этот код также называется кодом Хэмминга.

Пример 2.10. Построить расширенный код Хэмминга с параметрами (2^l-1,2^l-l)=(2⁴,2⁴-4)=(16,11,4), если исходный код Хэмминга имеет параметры (2^l-1,2^l-1-l)=(2⁴-1, 2⁴-1-4)=(15,11,3), и проверочная матрица имеет следующее построение:

H_4,15(x) =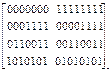

Решение:

а) в каждую кодовую последовательность должен быть введен дополнительный проверочный символ, обозначим его через α₀, осуществляющий общую проверку на четность, т. е. α₀Åα₁Åα₂Å…Åα_n=0;

б) введение этого дополнительного проверочного символа необходимо учесть в проверочной матрице исходного кода путем приписывания слева логического нуля к каждой строке исходной матрицы, т. е. впереди каждой строки приписать нулевой символ;

в) к получившимся строкам матрицы сверху приписывается строка, состоящая из одних логических единиц. Следовательно, проверочная матрица будет иметь следующее построение:

H_5,16(x) =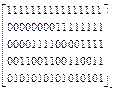

При использовании стандартного алгоритма декодирования и при наличии ошибок возможны две основные ситуации:

– первая – синдром совпадает с одним из столбцов матрицы H_5,16(x) и тогда ошибка исправляется. В случае одиночной ошибки добавленное равенство α₀Åα₁Åα₂Å…Åα_n=0 нарушается, а остальные синдромные символы S₁,S₂,S₃,S₄ – образуют номер позиции столбца проверочной матрицы H_5,16(x) и, следовательно, номер ошибочного информационного символа;

– вторая – синдром не совпадает ни с одним из столбцов матрицы H_5,16(x) и синдром не равен нулю. Это означает, что в кодовой последовательности имеются две ошибки. Если произойдут две ошибки или более, то равенство α₀Åα₁Åα₂Å…Åα_n=0 не нарушается, а структура синдрома S₁…S₄ не совпадет ни с одним из столбцов матрицы H_5,16(x) и не будет неравной нулю. Полученный (n,k,d₀)=(16,11,4)- код Хэмминга уже является нециклическим кодом.

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Date: 2015-09-22; view: 972; Нарушение авторских прав

mydocx.ru - 2015-2025 year. (0.011 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию