
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Полный дифференциал функции нескольких переменных
|
|
Пусть на области D задана функция двух переменных z =f(х,у), M0(x0;y0) - внутренняя точка области D, M(x0+Δx;y+Δy) - "соседняя" с M0 точка из D.
Рассмотрим полное приращение функции:
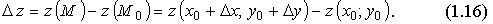
Если Δz представлено в виде:
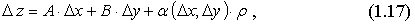
где A, B - постоянные (не зависящие от Δx, Δy), 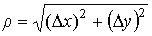 - расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx
- расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx 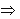 0, Δy
0, Δy 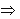 0; тогда функция z =f(х,у) называется дифференцируемой в точке M0, а выражение
0; тогда функция z =f(х,у) называется дифференцируемой в точке M0, а выражение
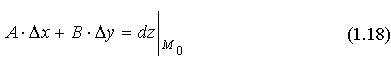
называется полным дифференциалом функции z =f(х;у) в точке M0.
Теорема 1.1. Если z =f(х;у) дифференцируема в точке M0, то
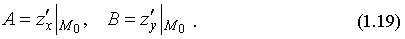
Частной производной от функции 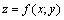 по независимой переменной по независимой переменной 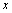 называется производная называется производная
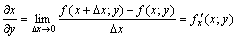 , вычисленная при постоянном , вычисленная при постоянном 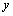 .
Частной производной по y называется производная .
Частной производной по y называется производная 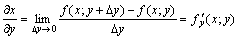 , вычисленная при постоянном , вычисленная при постоянном 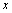 . Для частных производных справедливы обычные правила и формулы дифференцирования. . Для частных производных справедливы обычные правила и формулы дифференцирования.
|
52. Означення подвійного та повторного інтегралів. Обчислення подвійного інтеграла.
Означення подвійного інтеграла одночасно дає і спосіб його обчислення. Однак цей спосіб досить складний, тому розглянемо інший, який зводиться до обчислення так званого повторного інтеграла 

 двох визначених інтегралів.
двох визначених інтегралів.
Якщо 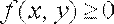 для
для 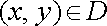

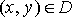
 , то подвійний інтеграл
, то подвійний інтеграл 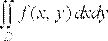 виражає об’єм циліндричного тіла з основою
виражає об’єм циліндричного тіла з основою 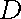
 , обмеженого поверхнею
, обмеженого поверхнею 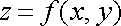
 та циліндричною поверхнею, твірні якої паралельні осі
та циліндричною поверхнею, твірні якої паралельні осі 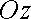
 , а напрямною є межа області
, а напрямною є межа області 
 (рис. 4).
(рис. 4).
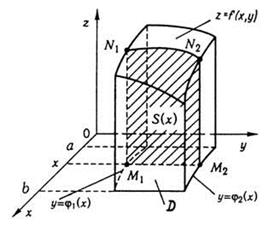
Рис. 4
Обчислимо цей об’єм за допомогою методу паралельних перерізів
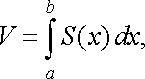 (10)
(10) 
де 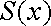



 площа перерізу тіла площиною, перпендикулярною до осі
площа перерізу тіла площиною, перпендикулярною до осі 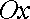
 , а
, а 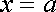
 та
та 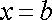



 рівняння площин, що обмежують задане тіло.
рівняння площин, що обмежують задане тіло.
Спочатку розглянемо випадок, коли область 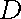
 обмежена прямими
обмежена прямими 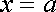
 ,
, 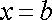
 , де
, де 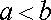
 , та неперервними кривими
, та неперервними кривими 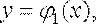


 , причому
, причому 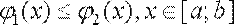
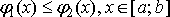
 (рис. 5).
(рис. 5).
Провівши через точку 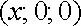
 (
(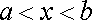
 ), перпендикулярну до осі
), перпендикулярну до осі 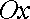

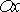
 площину, дістанемо у перерізі криволінійну трапецію
площину, дістанемо у перерізі криволінійну трапецію 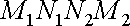
 , яка перетне область
, яка перетне область 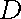
 по прямій
по прямій 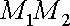
 . Точку
. Точку 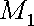
 називатимемо точкою входу в область
називатимемо точкою входу в область 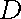
 , а точку
, а точку 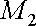



 точкою виходу з неї. Їх ординати позначимо відповідно
точкою виходу з неї. Їх ординати позначимо відповідно 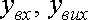
 . Тоді
. Тоді 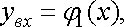

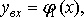

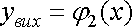

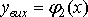
 .
.
Визначена таким чином область називається правильною в напрямі осі 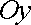
 .
.
Означення. Область 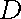
 називається правильною в напрямі осі
називається правильною в напрямі осі 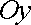
 (осі
(осі 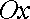 ), якщо довільна пряма, яка проходить через внутрішню точку області
), якщо довільна пряма, яка проходить через внутрішню точку області 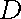
 паралельно осі
паралельно осі 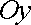
 (осі
(осі 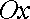
 ), перетинає межу області не більше, ніж у двох точках.
), перетинає межу області не більше, ніж у двох точках.
Правильна область в напрямі осі 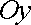
 зображена на рис. 5, а правильна область в напрямі осі
зображена на рис. 5, а правильна область в напрямі осі 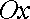



 на рис. 6.
на рис. 6.
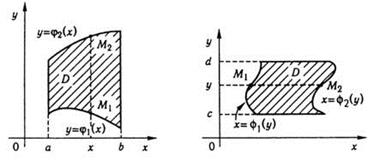
Рис. 5 Рис. 6
Площа 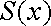

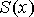
 трапеції
трапеції 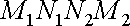

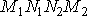
 дорівнює визначеному інтегралу
дорівнює визначеному інтегралу
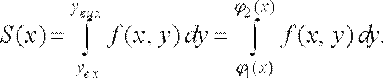

Підставляючи у рівність (10) вираз для 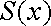 , дістанемо
, дістанемо
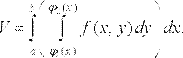


Оскільки об’єм 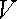

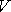
 циліндричного тіла дорівнює подвійному інтегралу
циліндричного тіла дорівнює подвійному інтегралу 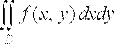
 , то маємо
, то маємо
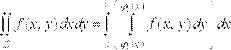
 або
або 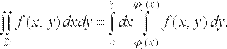 (11)
(11)
Праву частину формули (11) називають повторним інтегралом від функції 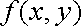


 по області
по області 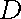

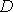
 . У повторному інтегралі (11) інтегрування виконується спочатку по змінній
. У повторному інтегралі (11) інтегрування виконується спочатку по змінній 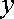

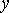
 (при цьому
(при цьому 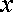


 вважається сталою), а потім по змінній
вважається сталою), а потім по змінній 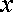


 . Інтеграл по змінній
. Інтеграл по змінній 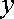

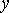
 називають внутрішнім, а по змінній
називають внутрішнім, а по змінній 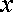





 зовнішнім. У результаті обчислення внутрішнього інтеграла одержуємо певну функцію від однієї змінної
зовнішнім. У результаті обчислення внутрішнього інтеграла одержуємо певну функцію від однієї змінної 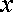


 . Інтегруючи цю функцію в межах від
. Інтегруючи цю функцію в межах від 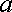


 до
до 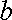

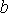
 , тобто обчислюючи зовнішній інтеграл, дістаємо деяке число
, тобто обчислюючи зовнішній інтеграл, дістаємо деяке число 

 значення подвійного інтеграла.
значення подвійного інтеграла.
Якщо область 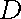

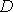
 обмежена двома неперервними кривими
обмежена двома неперервними кривими 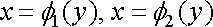
 і двома прямими
і двома прямими 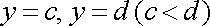
 , причому
, причому 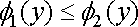
 для всіх
для всіх 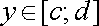
 , то справедлива формула
, то справедлива формула
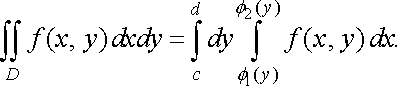 (12)
(12)
У формулі (12) внутрішнім є інтеграл по змінній 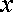


 . Обчислюючи його в межах від
. Обчислюючи його в межах від 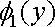

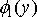
 до
до 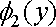

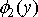
 (при цьому
(при цьому 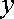

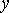
 вважається сталою), дістанемо деяку функцію від однієї змінної
вважається сталою), дістанемо деяку функцію від однієї змінної 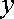

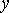
 . Інтегруючи потім цю функцію в межах від
. Інтегруючи потім цю функцію в межах від 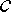


 до
до 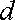

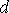
 , одержимо значення подвійного інтеграла.
, одержимо значення подвійного інтеграла.
Визначена таким чином область 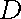

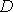
 є правильна в напрямі осі
є правильна в напрямі осі 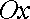
 .
.
Пропонуємо самостійно довести формулу (12), зробивши переріз циліндричного тіла перпендикулярною до осі 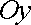
 площиною.
площиною.
Праві частини формул (11) і (12) також називають двократними інтегралами від функції 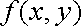
 по області
по області 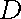
 .
.
Для зведення подвійного інтеграла до повторного потрібно побудувати область інтегрування 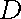
 , а потім визначити порядок інтегрування.
, а потім визначити порядок інтегрування.
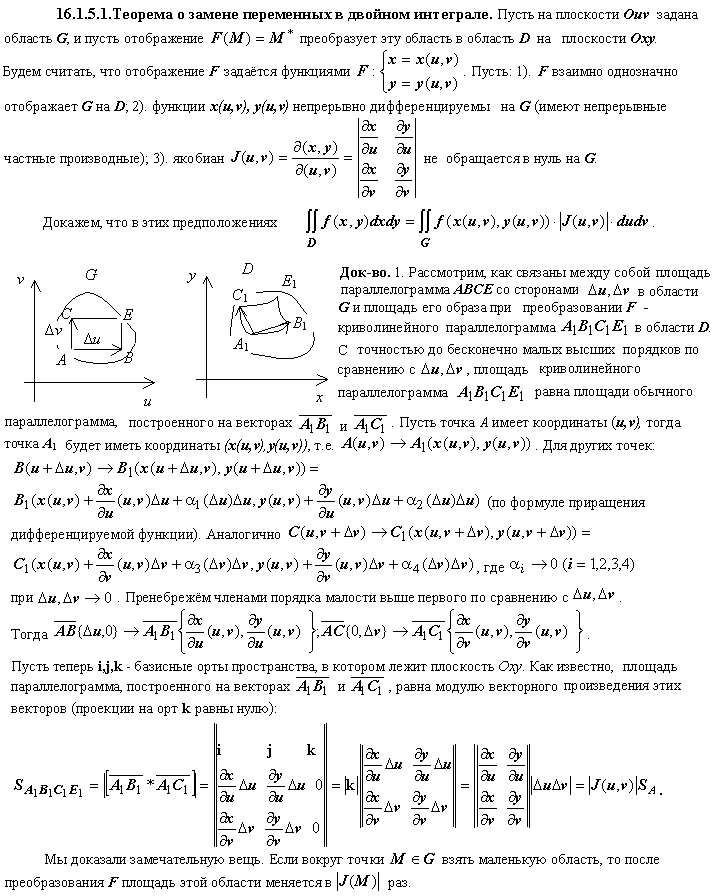
53. Заміна змінних у подвійному інтегралі.
Date: 2015-09-18; view: 505; Нарушение авторских прав